人教新课标B版必修3第三章3.2.1 古典概型 课件 23张PPT
文档属性
| 名称 | 人教新课标B版必修3第三章3.2.1 古典概型 课件 23张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 749.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 00:00:00 | ||
图片预览








文档简介
课件23张PPT。大 家 好 假设一个人把钱误存进了一张长期不用的银行卡中,并且他完全忘记了该卡的密码,问他在自动提款机上随机地输入密码,一次就能取出钱的概率是多少?密码是……想一想3.2.1古典概型高中数学必修③人教B版1、能说出古典概型的两大特点
2、会用古典概型进行概率计算
3、通过对现实生活中具体的概率问题的探究,感知应用数学解决问题的方法,体会数学知识与现实世界的联系,培养逻辑推理能力。教学目标1、掷一枚质地均匀的硬币的试验,
(1)可能出现几种不同的结果? (2)哪一个面朝上的可能性较大?试验(一)一样大!概率都等于0.5试验(二) 2、抛掷一只均匀的骰子一次。
(1)点数朝上的试验结果是有限的还是无限的?
如果是有限的共有几种?
(2)哪一个点数朝上的可能性较大?一样大!试验(三)3、先后抛掷一枚质地均匀的硬币两次,观察正反面向上的情况.
这个试验的基本事件空间是什么?基本事件总数是几?
【提示】 基本事件空间为{(正,正),(正,反),(反,正),(反,反)},.
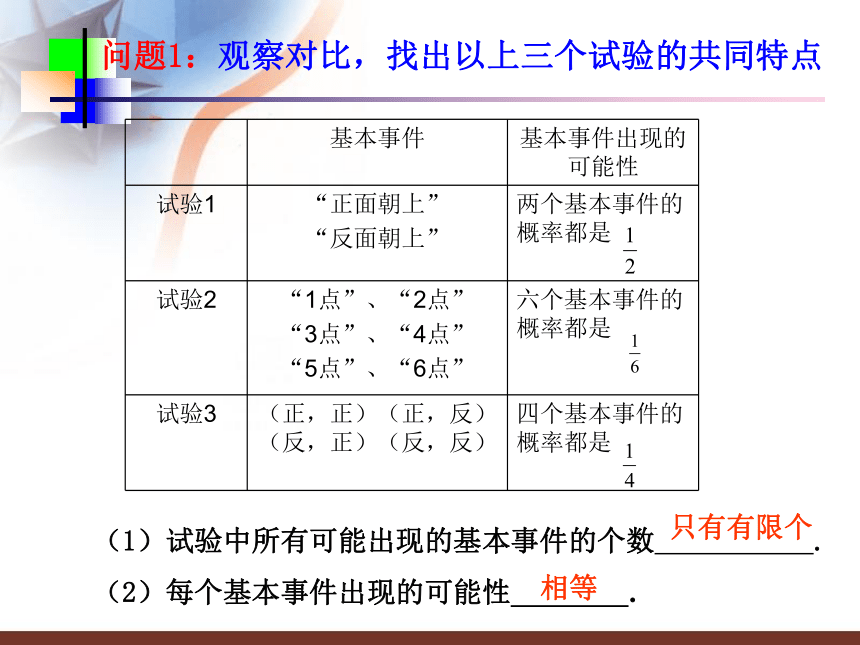
基本事件总数是4 问题1:观察对比,找出以上三个试验的共同特点(1)试验中所有可能出现的基本事件的个数 . 只有有限个相等(2)每个基本事件出现的可能性 .归纳总结我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型 。古典概型的定义:
(1)在一次试验中,可能出现的基本事件只有有限个(有限性)
(2)每个基本事件发生的可能性是均等的(等可能性) 下列试验中哪些是古典概型?
(1)先后抛掷两颗质地均匀的骰子,观察其朝上的点数.
(2).向一个圆面内随机地投射一个点,该点落在圆内任意一点都是等可能的。
(3).某同学随机地向一靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中5环和不中环。小试牛刀有限性等可能性有限性等可能性
在试验2中掷一颗均匀的骰子,事件A为“出现偶数点”请问事件A发生的概率是多少?问题2:在古典概型中,如何求随机事件出现的概率?
解析:基本事件总数为:1点,2点,3点,4点,5点,6点
事件A 包含的个基本事件:2点,4点,6点一般地,对于古典概型,如果试验的基本事件
总数为n, 随机事件A所包含的基本事件数为m,
我们就用 来描述事件A出现的可能性大小,称它为
事件A的概率,记作P(A),即有在古典概型中,
这一定义称为概率的古典定义典型例题例1:从含有两件正品 和一件次品 的3件产品中每次任取1件,每次取出后不放回,连续两次,求取出两件产品中恰有一件次品的概率。解析:每次取一个,取后不放回地连续取两次,其一切可能的结果组成的基本事件空间为用A表示“取出的两件中,恰好有一件为次品”这个事件,则事件A由4个基本事件组成,因而古典概型的概率计算步骤:(1)判断是否为古典概型;
(2)写出基本事件空间,计算基本事件的总数n.
(3)写出事件A所包含的基本事件,计算m.
(4)计算 归纳总结变式训练1:在例:1中,把“每次取出后不放回”这一条件换成“每次取出后放回”,其余条件不变,求取出的两件中恰好有一件次品的概率。典型例题由9个基本事件组成。由于每一件产品被取到的机会均等,因此可以认为这些基本事件出现是等可能的。解析:有放回地连续取出两次,其一切可能的结果组成的基本事件空间为事件B由4个基本事件组成,因而用B表示“恰有一件次品”这一事件,则例2:一先一后掷两个骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少? 解析:掷一个骰子的结果有6种,我们把两个骰子标上记号1,2以便区分,它总共出现的结果共有36种。典型例题(2)在上面的结果中,向上的点数之和为5的结果有4种,分别为:
(1,4),(2,3),(3,2),(4,1)。(3)由于所有36种结果是等可能的,其中向上点数之和为5的结果(记为事件A)有4种,则(1)从表中可以看出同时掷两个骰子的结果共有36种。典型例题变式训:2:做投掷二颗骰子试验,用(x,y)表示结果,其中x表示第一颗骰子出现的点数,y表示第二颗骰子出现的点数。
求:(1)事件“出现点数之和大于8”的概率是多少
(2)事件“出现点数相等”的概率是多少典型例题 假设一个人把钱误存进了一张长期不用的银行卡中,并且他完全忘记了该卡的密码,问他在自动提款机上随机地输入密码,一次就能取出钱的概率是多少?密码是……想一想课堂小结二、思想与方法
求某个随机事件A包含的基本事件的个数和试验中基本事件的总数的常用方法是列举法(或列表),应做到不重不漏一、知识点总结
1、古典概型的定义和特点
①有限性 ②等可能性
2、古典概型计算任何事件的概率计算公式
2、会用古典概型进行概率计算
3、通过对现实生活中具体的概率问题的探究,感知应用数学解决问题的方法,体会数学知识与现实世界的联系,培养逻辑推理能力。教学目标1、掷一枚质地均匀的硬币的试验,
(1)可能出现几种不同的结果? (2)哪一个面朝上的可能性较大?试验(一)一样大!概率都等于0.5试验(二) 2、抛掷一只均匀的骰子一次。
(1)点数朝上的试验结果是有限的还是无限的?
如果是有限的共有几种?
(2)哪一个点数朝上的可能性较大?一样大!试验(三)3、先后抛掷一枚质地均匀的硬币两次,观察正反面向上的情况.
这个试验的基本事件空间是什么?基本事件总数是几?
【提示】 基本事件空间为{(正,正),(正,反),(反,正),(反,反)},.
基本事件总数是4 问题1:观察对比,找出以上三个试验的共同特点(1)试验中所有可能出现的基本事件的个数 . 只有有限个相等(2)每个基本事件出现的可能性 .归纳总结我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型 。古典概型的定义:
(1)在一次试验中,可能出现的基本事件只有有限个(有限性)
(2)每个基本事件发生的可能性是均等的(等可能性) 下列试验中哪些是古典概型?
(1)先后抛掷两颗质地均匀的骰子,观察其朝上的点数.
(2).向一个圆面内随机地投射一个点,该点落在圆内任意一点都是等可能的。
(3).某同学随机地向一靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中5环和不中环。小试牛刀有限性等可能性有限性等可能性
在试验2中掷一颗均匀的骰子,事件A为“出现偶数点”请问事件A发生的概率是多少?问题2:在古典概型中,如何求随机事件出现的概率?
解析:基本事件总数为:1点,2点,3点,4点,5点,6点
事件A 包含的个基本事件:2点,4点,6点一般地,对于古典概型,如果试验的基本事件
总数为n, 随机事件A所包含的基本事件数为m,
我们就用 来描述事件A出现的可能性大小,称它为
事件A的概率,记作P(A),即有在古典概型中,
这一定义称为概率的古典定义典型例题例1:从含有两件正品 和一件次品 的3件产品中每次任取1件,每次取出后不放回,连续两次,求取出两件产品中恰有一件次品的概率。解析:每次取一个,取后不放回地连续取两次,其一切可能的结果组成的基本事件空间为用A表示“取出的两件中,恰好有一件为次品”这个事件,则事件A由4个基本事件组成,因而古典概型的概率计算步骤:(1)判断是否为古典概型;
(2)写出基本事件空间,计算基本事件的总数n.
(3)写出事件A所包含的基本事件,计算m.
(4)计算 归纳总结变式训练1:在例:1中,把“每次取出后不放回”这一条件换成“每次取出后放回”,其余条件不变,求取出的两件中恰好有一件次品的概率。典型例题由9个基本事件组成。由于每一件产品被取到的机会均等,因此可以认为这些基本事件出现是等可能的。解析:有放回地连续取出两次,其一切可能的结果组成的基本事件空间为事件B由4个基本事件组成,因而用B表示“恰有一件次品”这一事件,则例2:一先一后掷两个骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少? 解析:掷一个骰子的结果有6种,我们把两个骰子标上记号1,2以便区分,它总共出现的结果共有36种。典型例题(2)在上面的结果中,向上的点数之和为5的结果有4种,分别为:
(1,4),(2,3),(3,2),(4,1)。(3)由于所有36种结果是等可能的,其中向上点数之和为5的结果(记为事件A)有4种,则(1)从表中可以看出同时掷两个骰子的结果共有36种。典型例题变式训:2:做投掷二颗骰子试验,用(x,y)表示结果,其中x表示第一颗骰子出现的点数,y表示第二颗骰子出现的点数。
求:(1)事件“出现点数之和大于8”的概率是多少
(2)事件“出现点数相等”的概率是多少典型例题 假设一个人把钱误存进了一张长期不用的银行卡中,并且他完全忘记了该卡的密码,问他在自动提款机上随机地输入密码,一次就能取出钱的概率是多少?密码是……想一想课堂小结二、思想与方法
求某个随机事件A包含的基本事件的个数和试验中基本事件的总数的常用方法是列举法(或列表),应做到不重不漏一、知识点总结
1、古典概型的定义和特点
①有限性 ②等可能性
2、古典概型计算任何事件的概率计算公式
