人教新课标B版必修三第二章2.2.2 用样本的数字特征估计总体的数字特征 课件 24张PPT
文档属性
| 名称 | 人教新课标B版必修三第二章2.2.2 用样本的数字特征估计总体的数字特征 课件 24张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 782.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 00:00:00 | ||
图片预览




文档简介
课件24张PPT。 2.2 用样本估计总体2.2.2用样本的数字特征估计总体的数字特征抽样是统计的第一步,接下来就要对样本进行分析 温故知新:初中统计部分曾学过用什么来反映总体的水平?
用什么来考察稳定程度?它们是怎么定义的?1、众数:在一组数据中,出现次数最多的数据叫做
这组数据的众数在初中我们学过用平均数、众数和中位数反映总体的水平,用方差考察稳定程度。2、中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数众数、中位数、平均数都是描述一组数据的集中趋势的特征数,本节课就学习如何利用频率分布直方图求众数、中位数、平均数?
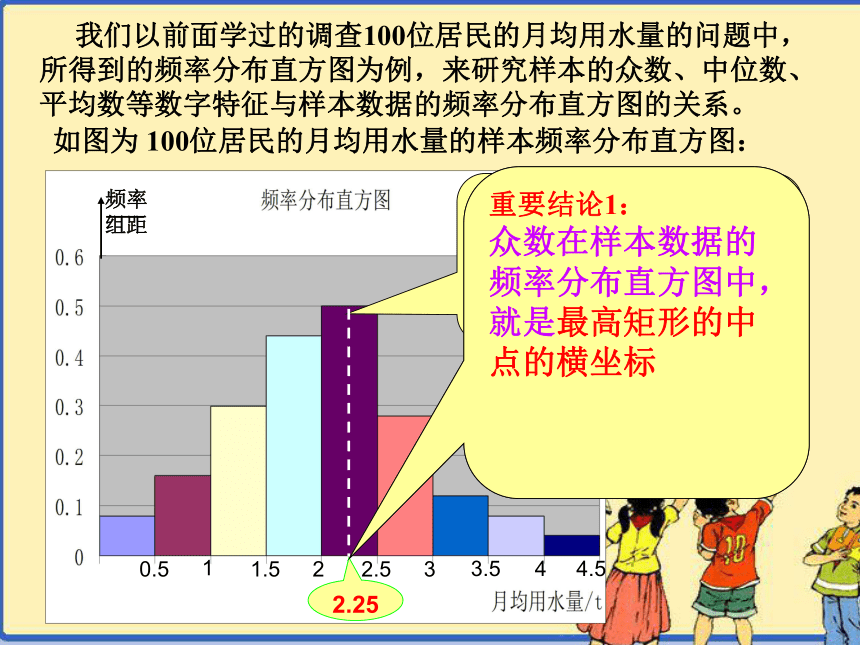
频率分布直方图的关系众数、中位数、平均数与 我们以前面学过的调查100位居民的月均用水量的问题中,
所得到的频率分布直方图为例,来研究样本的众数、中位数、
平均数等数字特征与样本数据的频率分布直方图的关系。思考1:图中最高的小长方形的含义是什么?由此你是否能得 出众数是几?
图中最高的小长方形的含义是样本数据落在[2,2.5)的最多,所以众数一定在[2,2.5)内,因为在[2,2.5) 内的数据较多,于是通常取该区间的两个端点的平均数作为众数,即
众数是2.25
2.25重要结论1:
众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标
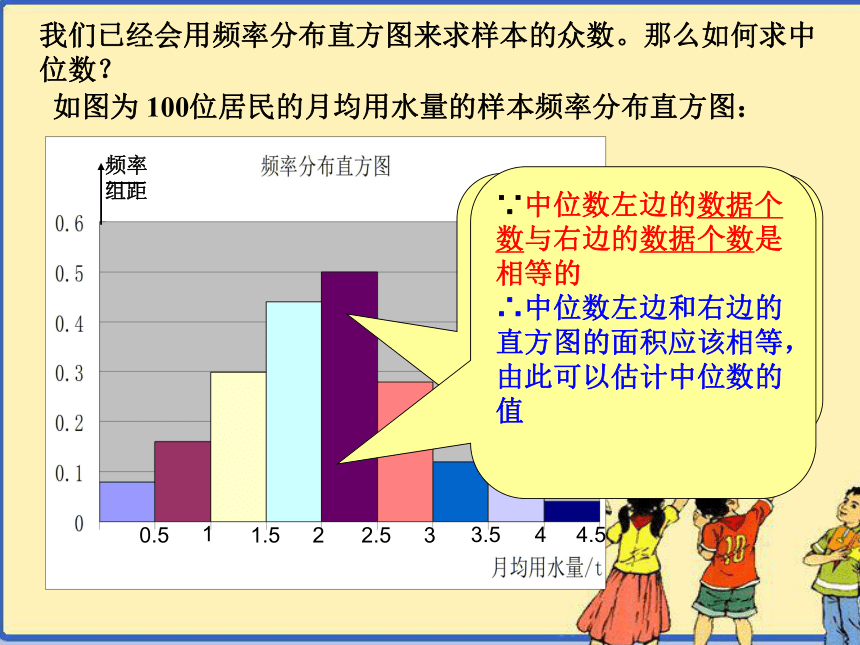
我们已经会用频率分布直方图来求样本的众数。那么如何求中位数?思考2:根据中位数的定义知道:在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,由此你是否能求出中位数是几?
∵中位数左边的数据个数与右边的数据个数是相等的
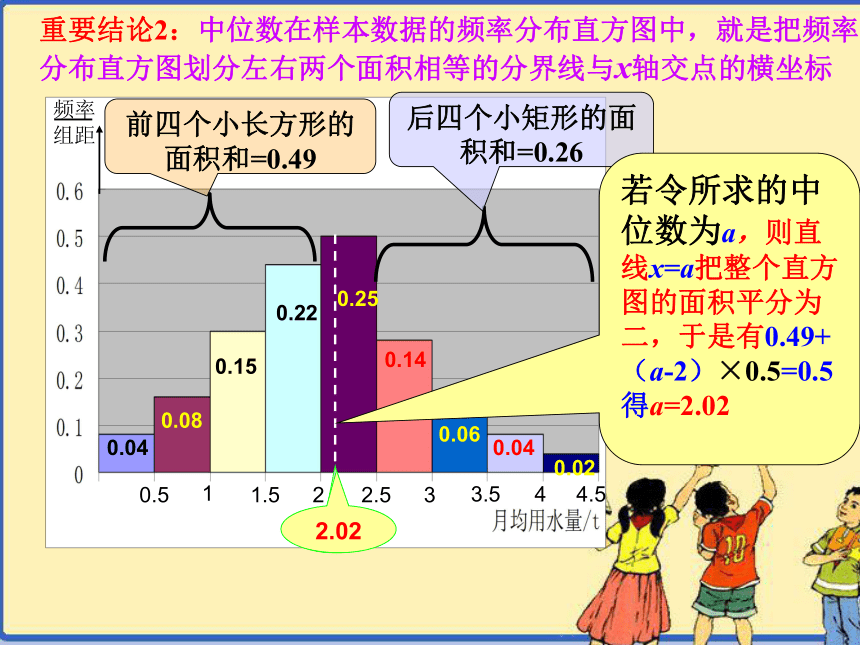
∴中位数左边和右边的直方图的面积应该相等,由此可以估计中位数的值 0.040.080.150.220.250.140.060.040.02前四个小长方形的面积和=0.49后四个小矩形的面积和=0.26
若令所求的中位数为a,则直线x=a把整个直方图的面积平分为二,于是有0.49+ (a-2)×0.5=0.5得a=2.02
2.02重要结论2:中位数在样本数据的频率分布直方图中,就是把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标 中位数一定在最高的小长方形内取得吗?∵最高的小长方形左右两边的小长方形的面积和分别都不会达到0.5
∴结论:中位数一定在最高的小长方形内取得,但是不一定是该区间的两个端点的平均数,即有可能比平均数大,也可能比平均数小 0.040.080.150.220.250.140.060.040.02我们已经会用频率分布直方图来求出了样本的众数和中位数,那么最后如何求平均数?思考1:在频率分布直方图中,各个组的平均数如何找?
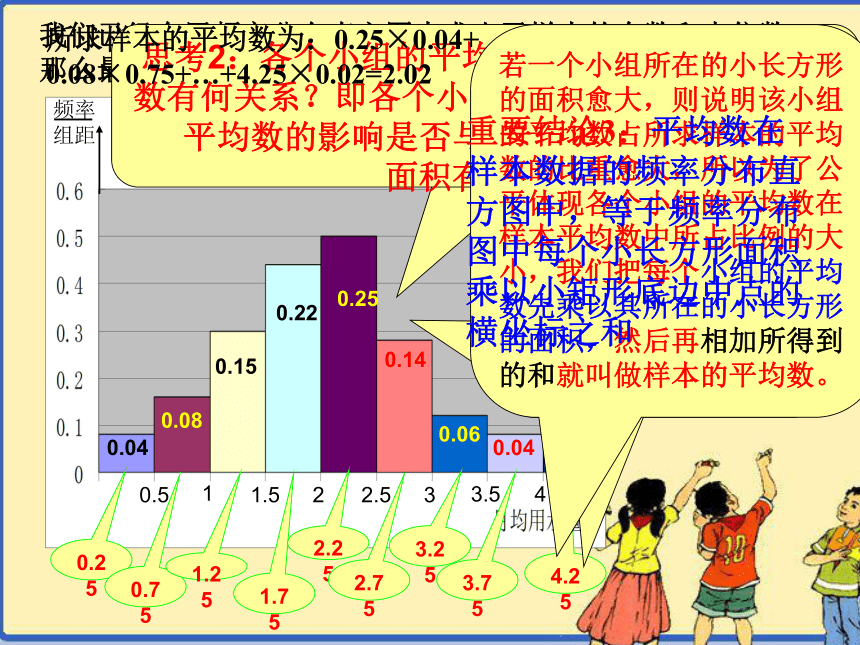
在频率分布直方图中,各个组的平均数用其区间的中点表示即区间的两个端点之和的一半
0.250.751.251.752.252.753.253.754.25思考2:各个小组的平均数与所求的样本的平均数有何关系?即各个小组的平均数对所求样本的平均数的影响是否与其所在的小长方形的
面积有关系?若一个小组所在的小长方形的面积愈大,则说明该小组的平均数占所求样本的平均数的比重愈大,所以为了公平体现各个小组的平均数在样本平均数中所占比例的大小,我们把每个小组的平均数先乘以其所在的小长方形的面积,然后再相加所得到的和就叫做样本的平均数。所求样本的平均数为:0.25×0.04+
0.08×0.75+…+4.25×0.02=2.02重要结论3:平均数在样本数据的频率分布直方图中,等于频率分布图中每个小长方形面积乘以小矩形底边中点的横坐标之和 例.某校从参加高三模拟考试的学生中随机抽取60名
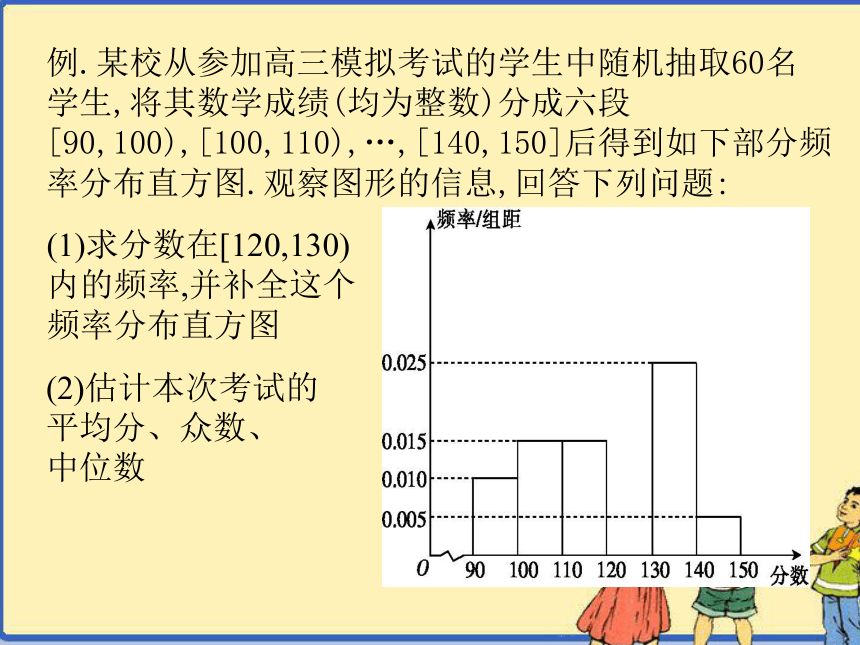
学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)求分数在[120,130)内的频率,并补全这个频率分布直方图(2)估计本次考试的
平均分、众数、
中位数 ?补全后的直方图如图:【解析】(1)分数在[120,130)内的频率为:
1-(0.1+0.15+0.15+0.25+0.05)=1-0.7=0.3中位数为:
10×(0.01+0.015+0.015)+
(x-120)×0.03=0.5解得
x=123.3平均分为: 95×0.1+105×0.15+115×
0.15+125×0.3+135×0.25+
145×0.05=121(2)众数为125 1.某校举行了由全部学生参加的校园安全知识考试,
从中抽出60名学生,将其成绩分成六段[40,50),[50,60),…,[90,100)后,画出如图所示的频率
分布直方图.估计这次考试的及格率(60分及以上为
及格)为________;平均分为________ 巩固练习 解析 及格的各组的频率是(0.015+0.03+0.025+0.005)×10=0.75,即及格率约为75%;
样本的均值为45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71,
以这个分数估计总体的分数即得总体的平均分数约为71.
答案 75% 71 巩固练习B 3.某校从参加高一年级期末考试的学生中抽出60名
学生,将其成绩(均为整数)分成六段[40,50),[50,60),
…,[90,100]后画出如下部分频率分布直方图.
估计这次考试的及格率(60分及以上为及格)和平均分 解:依题意60及以上的分数所在的第三、四、五、六组的频率和为
(0.015+0.03+0.025+0.005)×10=0.75
∴抽样学生成绩的合格率是75%.
利用频率分布表估算抽样学生的平均分:
45·f1+55·f2+65·f3+75·f4+85·f5+95·f6
=45×0.1+55×0.15×+65×0.15+75×0.3+
85×0.25+95×0.05=71.
∴估计这次考试的平均分是71分 4.(2012广东)某班100名学生期中考试语文成绩的频率分布直
方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数. 【思路点拨】(1)根据各小长方形的面积和为1,求a;
(2)借助频率分布直方图的中点估计平均分.
(3)先求语文成绩在各段的人数,进而求数学成绩在[50,90)之外的人数.【解答】(1)由频率分布直方图知(0.04+0.03+0.02+2a)×10=1
因此a=0.005(2) ∵55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73
∴平均分为73分(3)分别求出语文成绩分数段在[50,60),[60,70),[70,80),[80,90)的人数依次为0.05×100=5,0.4×100=40,
0.3×100=30,0.2×100=20所以数学成绩分数段在[50,60),[60,70),[70,80),[80,90)的人数依次为5,20,40,25所以数学成绩在[50,90)之外的人数有100-(5+20+40+25)=10(人) ?例2 某校从参加高三模拟考试的学生中随机抽取60名学生,将
其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得 到如下部分频率分布直方图.观察图形的信息,回答下列问题:考纲解读命题预测知识盘点典例精析技巧归纳真题探究基础拾遗例题备选(1)求分数在[120,130)内的频率,并补全这个频率分布直方图;(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估 计本次考试的平均分.考纲解读命题预测知识盘点典例精析技巧归纳真题探究基础拾遗例题备选五、课堂小结
1. 用样本的数字特征估计总体的数字特征分两类:
(1)用样本平均数估计总体平均数.
(2)用样本标准差估计总体标准差.样本容量越大,估计就越精确.
2. 平均数对数据有“取齐”的作用,代表一组数据的平均水平.
3. 标准差描述一组数据围绕平均数波动的大小,反映了一组数据变化的幅度.
布置作业:1、《课本》第74页习题2.2 A组:1、22、《学习指导》第43页 例2
用什么来考察稳定程度?它们是怎么定义的?1、众数:在一组数据中,出现次数最多的数据叫做
这组数据的众数在初中我们学过用平均数、众数和中位数反映总体的水平,用方差考察稳定程度。2、中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数众数、中位数、平均数都是描述一组数据的集中趋势的特征数,本节课就学习如何利用频率分布直方图求众数、中位数、平均数?
频率分布直方图的关系众数、中位数、平均数与 我们以前面学过的调查100位居民的月均用水量的问题中,
所得到的频率分布直方图为例,来研究样本的众数、中位数、
平均数等数字特征与样本数据的频率分布直方图的关系。思考1:图中最高的小长方形的含义是什么?由此你是否能得 出众数是几?
图中最高的小长方形的含义是样本数据落在[2,2.5)的最多,所以众数一定在[2,2.5)内,因为在[2,2.5) 内的数据较多,于是通常取该区间的两个端点的平均数作为众数,即
众数是2.25
2.25重要结论1:
众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标
我们已经会用频率分布直方图来求样本的众数。那么如何求中位数?思考2:根据中位数的定义知道:在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,由此你是否能求出中位数是几?
∵中位数左边的数据个数与右边的数据个数是相等的
∴中位数左边和右边的直方图的面积应该相等,由此可以估计中位数的值 0.040.080.150.220.250.140.060.040.02前四个小长方形的面积和=0.49后四个小矩形的面积和=0.26
若令所求的中位数为a,则直线x=a把整个直方图的面积平分为二,于是有0.49+ (a-2)×0.5=0.5得a=2.02
2.02重要结论2:中位数在样本数据的频率分布直方图中,就是把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标 中位数一定在最高的小长方形内取得吗?∵最高的小长方形左右两边的小长方形的面积和分别都不会达到0.5
∴结论:中位数一定在最高的小长方形内取得,但是不一定是该区间的两个端点的平均数,即有可能比平均数大,也可能比平均数小 0.040.080.150.220.250.140.060.040.02我们已经会用频率分布直方图来求出了样本的众数和中位数,那么最后如何求平均数?思考1:在频率分布直方图中,各个组的平均数如何找?
在频率分布直方图中,各个组的平均数用其区间的中点表示即区间的两个端点之和的一半
0.250.751.251.752.252.753.253.754.25思考2:各个小组的平均数与所求的样本的平均数有何关系?即各个小组的平均数对所求样本的平均数的影响是否与其所在的小长方形的
面积有关系?若一个小组所在的小长方形的面积愈大,则说明该小组的平均数占所求样本的平均数的比重愈大,所以为了公平体现各个小组的平均数在样本平均数中所占比例的大小,我们把每个小组的平均数先乘以其所在的小长方形的面积,然后再相加所得到的和就叫做样本的平均数。所求样本的平均数为:0.25×0.04+
0.08×0.75+…+4.25×0.02=2.02重要结论3:平均数在样本数据的频率分布直方图中,等于频率分布图中每个小长方形面积乘以小矩形底边中点的横坐标之和 例.某校从参加高三模拟考试的学生中随机抽取60名
学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)求分数在[120,130)内的频率,并补全这个频率分布直方图(2)估计本次考试的
平均分、众数、
中位数 ?补全后的直方图如图:【解析】(1)分数在[120,130)内的频率为:
1-(0.1+0.15+0.15+0.25+0.05)=1-0.7=0.3中位数为:
10×(0.01+0.015+0.015)+
(x-120)×0.03=0.5解得
x=123.3平均分为: 95×0.1+105×0.15+115×
0.15+125×0.3+135×0.25+
145×0.05=121(2)众数为125 1.某校举行了由全部学生参加的校园安全知识考试,
从中抽出60名学生,将其成绩分成六段[40,50),[50,60),…,[90,100)后,画出如图所示的频率
分布直方图.估计这次考试的及格率(60分及以上为
及格)为________;平均分为________ 巩固练习 解析 及格的各组的频率是(0.015+0.03+0.025+0.005)×10=0.75,即及格率约为75%;
样本的均值为45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71,
以这个分数估计总体的分数即得总体的平均分数约为71.
答案 75% 71 巩固练习B 3.某校从参加高一年级期末考试的学生中抽出60名
学生,将其成绩(均为整数)分成六段[40,50),[50,60),
…,[90,100]后画出如下部分频率分布直方图.
估计这次考试的及格率(60分及以上为及格)和平均分 解:依题意60及以上的分数所在的第三、四、五、六组的频率和为
(0.015+0.03+0.025+0.005)×10=0.75
∴抽样学生成绩的合格率是75%.
利用频率分布表估算抽样学生的平均分:
45·f1+55·f2+65·f3+75·f4+85·f5+95·f6
=45×0.1+55×0.15×+65×0.15+75×0.3+
85×0.25+95×0.05=71.
∴估计这次考试的平均分是71分 4.(2012广东)某班100名学生期中考试语文成绩的频率分布直
方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数. 【思路点拨】(1)根据各小长方形的面积和为1,求a;
(2)借助频率分布直方图的中点估计平均分.
(3)先求语文成绩在各段的人数,进而求数学成绩在[50,90)之外的人数.【解答】(1)由频率分布直方图知(0.04+0.03+0.02+2a)×10=1
因此a=0.005(2) ∵55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73
∴平均分为73分(3)分别求出语文成绩分数段在[50,60),[60,70),[70,80),[80,90)的人数依次为0.05×100=5,0.4×100=40,
0.3×100=30,0.2×100=20所以数学成绩分数段在[50,60),[60,70),[70,80),[80,90)的人数依次为5,20,40,25所以数学成绩在[50,90)之外的人数有100-(5+20+40+25)=10(人) ?例2 某校从参加高三模拟考试的学生中随机抽取60名学生,将
其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得 到如下部分频率分布直方图.观察图形的信息,回答下列问题:考纲解读命题预测知识盘点典例精析技巧归纳真题探究基础拾遗例题备选(1)求分数在[120,130)内的频率,并补全这个频率分布直方图;(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估 计本次考试的平均分.考纲解读命题预测知识盘点典例精析技巧归纳真题探究基础拾遗例题备选五、课堂小结
1. 用样本的数字特征估计总体的数字特征分两类:
(1)用样本平均数估计总体平均数.
(2)用样本标准差估计总体标准差.样本容量越大,估计就越精确.
2. 平均数对数据有“取齐”的作用,代表一组数据的平均水平.
3. 标准差描述一组数据围绕平均数波动的大小,反映了一组数据变化的幅度.
布置作业:1、《课本》第74页习题2.2 A组:1、22、《学习指导》第43页 例2
