人教版数学六年级上册第八单元《数与形》精编测试题1(含答案)
文档属性
| 名称 | 人教版数学六年级上册第八单元《数与形》精编测试题1(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-09 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版数学六年级上册第八单元《数与形》精编测试题1
一、发现规律,填补空白。(共44分)
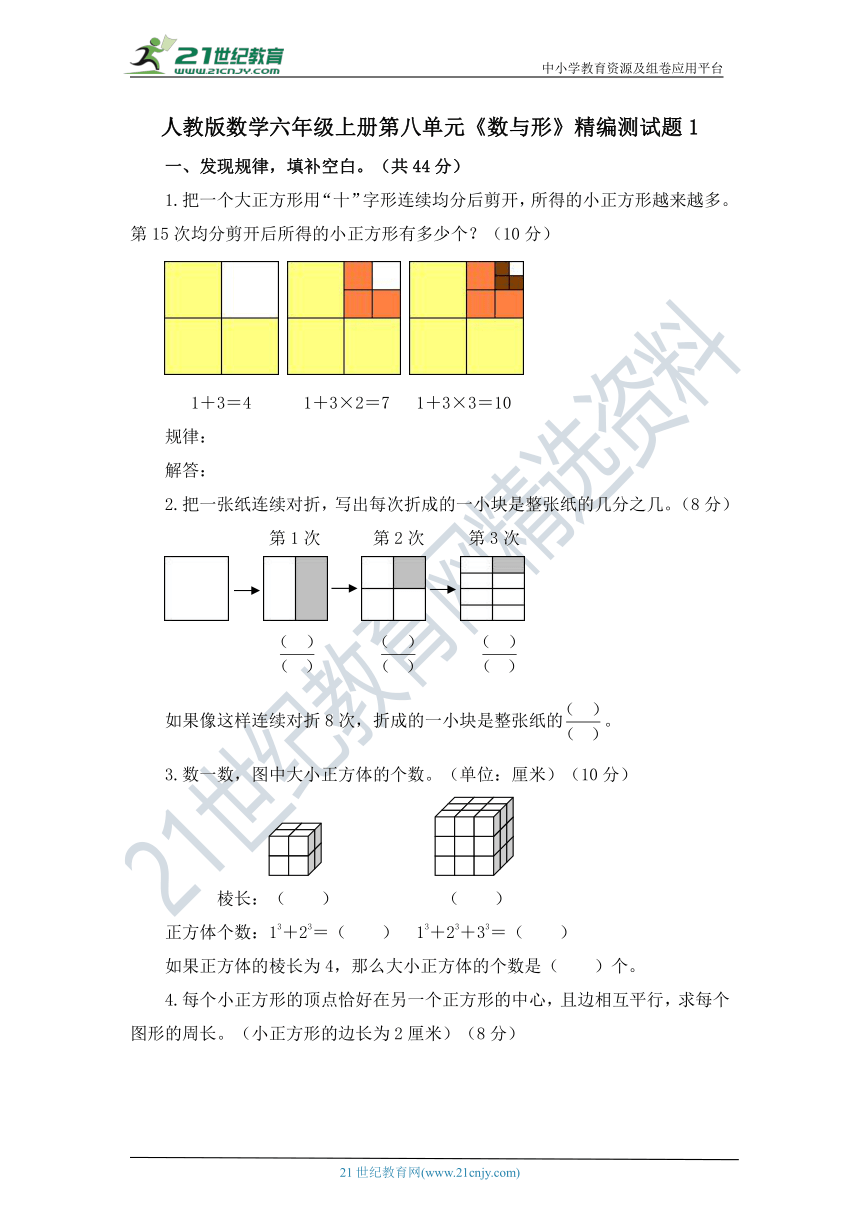
1.把一个大正方形用“十”字形连续均分后剪开,所得的小正方形越来越多。第15次均分剪开后所得的小正方形有多少个?(10分)
1+3=4 1+3×2=7 1+3×3=10
规律:
解答:
2.把一张纸连续对折,写出每次折成的一小块是整张纸的几分之几。(8分)
第1次 第2次 第3次
?Sheet1
一月 二月 三月
亚洲区 30 25 45
?
如果像这样连续对折8次,折成的一小块是整张纸的。
3.数一数,图中大小正方体的个数。(单位:厘米)(10分)
棱长:( ) ( )
正方体个数:13+23=( ) 13+23+33=( )
如果正方体的棱长为4,那么大小正方体的个数是( )个。
4.每个小正方形的顶点恰好在另一个正方形的中心,且边相互平行,求每个图形的周长。(小正方形的边长为2厘米)(8分)
( )厘米 ( )厘米 ( )厘米
若有8个小正方形像上面这样叠放,所组成的图形的周长是( )厘米。
5.随着三角形个数的增加,涂色三角形的个数也在增加。照这样接着画下去,第20个图形有( )个涂色的三角形。(8分)
1 3 6 10
二、想一想,选一选。(共16分,每题8分。)
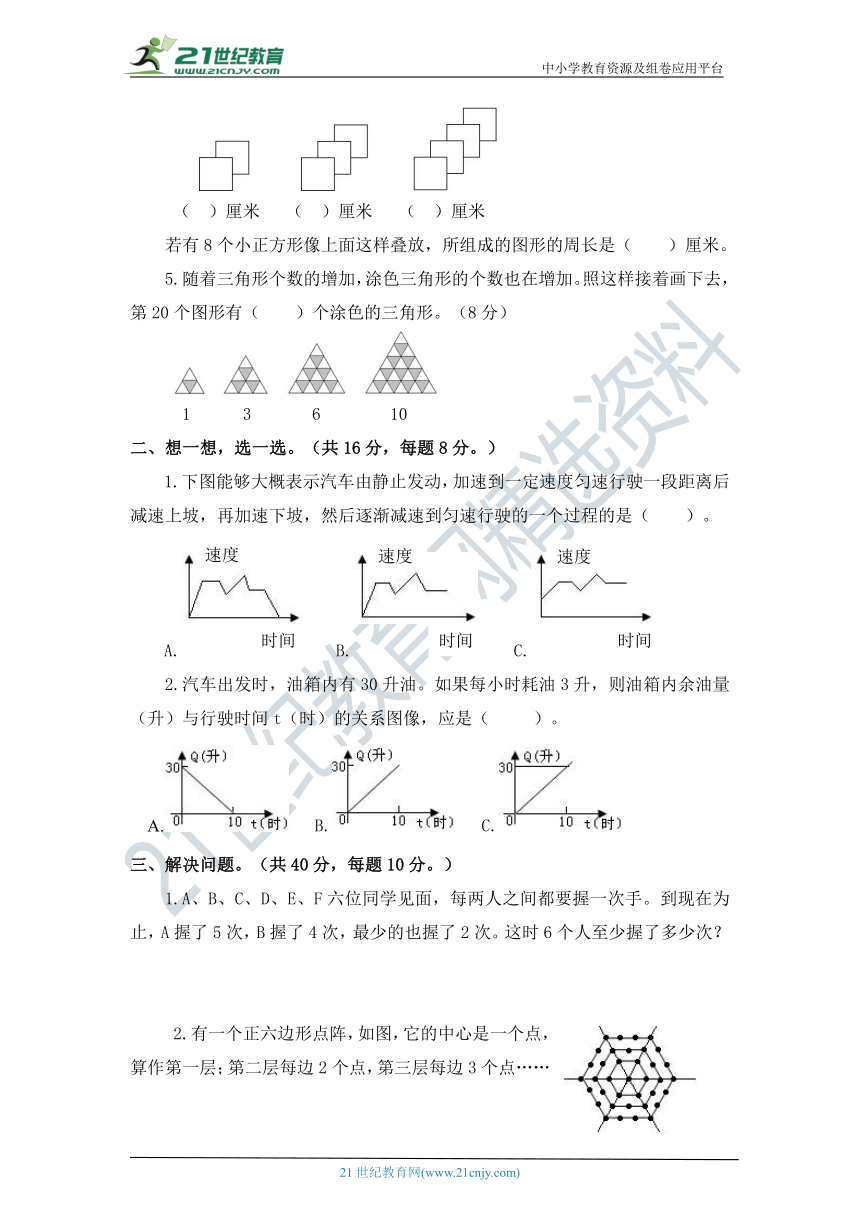
1.下图能够大概表示汽车由静止发动,加速到一定速度匀速行驶一段距离后减速上坡,再加速下坡,然后逐渐减速到匀速行驶的一个过程的是( )。
A. B. C.
2.汽车出发时,油箱内有30升油。如果每小时耗油3升,则油箱内余油量(升)与行驶时间t(时)的关系图像,应是( )。
A. B. C.
三、解决问题。(共40分,每题10分。)
1.A、B、C、D、E、F六位同学见面,每两人之间都要握一次手。到现在为止,A握了5次,B握了4次,最少的也握了2次。这时6个人至少握了多少次?
2.有一个正六边形点阵,如图,它的中心是一个点,算作第一层;第二层每边2个点,第三层每边3个点……这个六边形点阵第28层上面共有多少个点?第100层呢?
3.一条马路长180米,小明和他的小狗分别以均匀的速度同时从马路的起点出发。当小明走到马路的时,小狗已经到达马路的终点。然后返回与小明相向而行,遇到小明以后再跑向终点,达到终点以后再与小明相向而行……直到小明到达终点。小狗从出发开始,一共跑了多少米?
4.张伟在纸上画了四个点,如果把这四个点彼此连接成一个图形,这个图形中可能有几个三角形?
思考题。(共10分)
将自然数1,2,3,…按下图排列,照样子用一个方框框出九个数,这九个数的和能否等于2015?1998呢?如果能,请写出框中的最大数和最小数。
参考答案
一、1.每均分一次,正方形的个数增加3个;均分次,正方形的个数就增加3个。
1+3×15=46(个)
2.
3.2 9 3 36 100
4.12 16 20 36
5.210
二、1.B 2.A
三、1.18次
2.(28-1)×6=162(个)
(100-1)×6=594(个)
3.180÷=540(米)
4.8个 4个 3个 0个
思考题
仔细观察,可以发现方框中的九个数有这样的规律:横向三个数依次差1,纵向三个数依次差7。如果最小数为,则其余8个数依次为+1,+2,+7,+8,+9,+14,+15,+16。这九个数的和为9+72=9×(+8),所以九个数的和一定是9的倍数。
2015不是9的倍数,不能。
1998是9的倍数,能。9×(+8)=1998,=214。最大数是214+16=230。
速度
时间
速度
时间
速度
时间
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
