2.1.4 数乘向量 课件 20张PPT
文档属性
| 名称 | 2.1.4 数乘向量 课件 20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 605.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 00:00:00 | ||
图片预览







文档简介
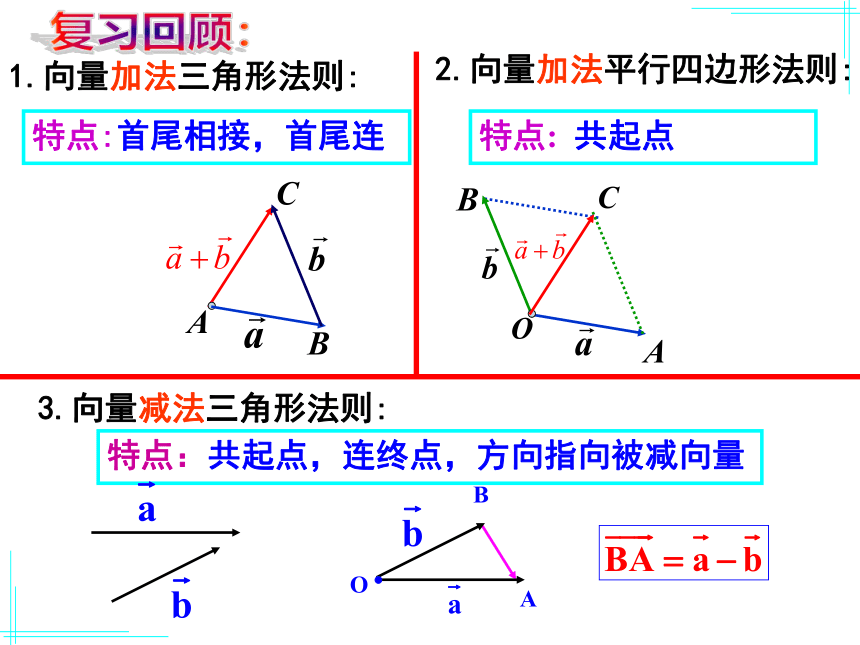
课件20张PPT。 2.1.4 数乘向量特点:共起点,连终点,方向指向被减向量1.向量加法三角形法则:特点:首尾相接,首尾连特点: 共起点2.向量加法平行四边形法则:3.向量减法三角形法则:复习回顾: 思考1:相同的几个数相加可以转化为数乘运算,如3+3+3+3+3=5×3=15.那么相等的几个向量相加是否也能转化为数乘运算呢?引入新课 思考2:已知非零向量 , 作出 和
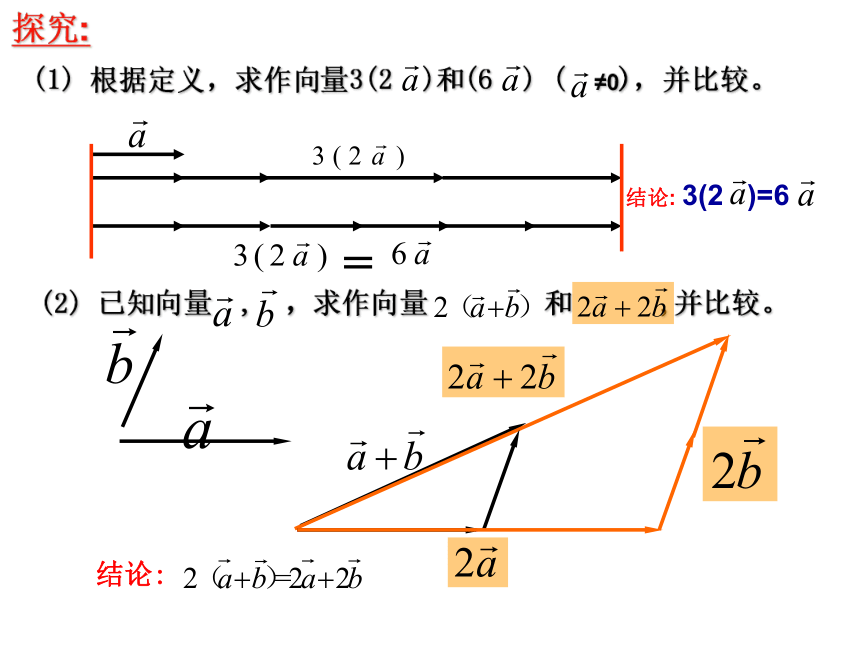
, 你能说明它们的几何意义吗? BACONMQP它的长度和方向规定如下:一.向量数乘的定义二、数乘向量的几何意义探究:特别的,我们有向量的加、减、数乘运算统称为向量的线性运算.结合律第一分配律第二分配律三、运算律:例1:C.A.B.(2).设 是非零向量, 是非零实数,下列结论正确的是( ).D.(1).下列四个说法正确的个数有( ).B.2个A.1个C.3个D.4个BC例2 计算下列各式 (2)
(3)解 : (1)例3:解:记 ①, ②练习2:解:因为(2)所以,所证等式成立则四边形ABCD是平行四边形,D是BC中点,则D也是AE中点.由向量加法平行四边形法则有解2:小 结一、①实数与向量可以相乘,其积仍是向量,
但实数与向量不能相加、相减.实数除以向量
没有意义,向量除以非零实数就是数乘向量.三、数乘向量运算律( C )分析:由 所以 在平行四边形ABCD中, ,M为BC的
中点,则 等于______ (1)(2)ABC课堂反馈:(3)课后思考: 教材P89课后训练;
完成教辅相关部分;
3.预习教材P90~92.课后作业数学使你聪颖
数学使你严谨
, 你能说明它们的几何意义吗? BACONMQP它的长度和方向规定如下:一.向量数乘的定义二、数乘向量的几何意义探究:特别的,我们有向量的加、减、数乘运算统称为向量的线性运算.结合律第一分配律第二分配律三、运算律:例1:C.A.B.(2).设 是非零向量, 是非零实数,下列结论正确的是( ).D.(1).下列四个说法正确的个数有( ).B.2个A.1个C.3个D.4个BC例2 计算下列各式 (2)
(3)解 : (1)例3:解:记 ①, ②练习2:解:因为(2)所以,所证等式成立则四边形ABCD是平行四边形,D是BC中点,则D也是AE中点.由向量加法平行四边形法则有解2:小 结一、①实数与向量可以相乘,其积仍是向量,
但实数与向量不能相加、相减.实数除以向量
没有意义,向量除以非零实数就是数乘向量.三、数乘向量运算律( C )分析:由 所以 在平行四边形ABCD中, ,M为BC的
中点,则 等于______ (1)(2)ABC课堂反馈:(3)课后思考: 教材P89课后训练;
完成教辅相关部分;
3.预习教材P90~92.课后作业数学使你聪颖
数学使你严谨
