3.2.2 半角的正弦、余弦和正切 课件 18张PPT
文档属性
| 名称 | 3.2.2 半角的正弦、余弦和正切 课件 18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 150.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 00:00:00 | ||
图片预览






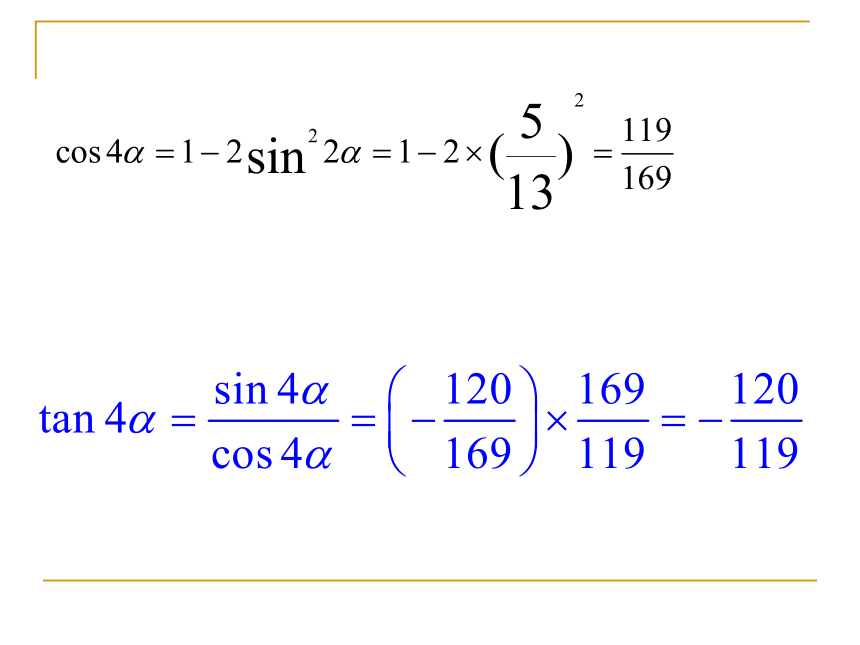
文档简介
课件18张PPT。3.1.3 二倍角的
正弦、余弦、正切公式( C(?+?) )
( C(? --?) )cos(?+?)= cos?cos?-sin?sin?
cos(?-?)= cos?cos?+sin?sin?( S(?+?) )
( S(?-?) )sin(?+?)= sin?cos?+cos?sin?
sin(?-?)= sin?cos?-cos?sin?( T(?+?) )
( T(?-?) )两角和与差的正弦、余弦、正切公式1.复习导入:思考:能利用S(?±?)、C(?±?)、 T(?±?)推导出sin2?,cos2?,tan2?的公式吗?在和角公式中,令?=?(换元思想)sin(?+?)= sin?cos? +cos?sin?sin2?= 2sin?cos? 同样cos(?+?)= cos?cos?-sin?sin?cos2?= cos2?-sin2?(S2?)(C2?)(T2?)2.倍角公式:解:3.典例分析:(1)sin4? = 2sin( )cos( )
(2)sin? = 2sin( )cos( )
(3)cos 6? = cos2( )-sin2( )
= 2cos2( )-1
= 1-2sin2( )
(4)cos25?-sin25?=cos( )2?2?3?3?3?3?10?4?4.公式巩固训练:解:方法一
分别算出tanA,tanB再求tan2A,tan2B,然后求tan(2A+2B)在△ABC中,0例3 求值 (1).sin22?30`cos22?30`6.变形公式:化简 例37知识引申例4证明倍角公式8.小结:变形公式:针对二倍角公式及变形公式要熟记公式,在
解题过程中要善于发现规律,学会灵活运用.9作业:谢谢指导!1课本P135.1-4
2
( C(? --?) )cos(?+?)= cos?cos?-sin?sin?
cos(?-?)= cos?cos?+sin?sin?( S(?+?) )
( S(?-?) )sin(?+?)= sin?cos?+cos?sin?
sin(?-?)= sin?cos?-cos?sin?( T(?+?) )
( T(?-?) )两角和与差的正弦、余弦、正切公式1.复习导入:思考:能利用S(?±?)、C(?±?)、 T(?±?)推导出sin2?,cos2?,tan2?的公式吗?在和角公式中,令?=?(换元思想)sin(?+?)= sin?cos? +cos?sin?sin2?= 2sin?cos? 同样cos(?+?)= cos?cos?-sin?sin?cos2?= cos2?-sin2?(S2?)(C2?)(T2?)2.倍角公式:解:3.典例分析:(1)sin4? = 2sin( )cos( )
(2)sin? = 2sin( )cos( )
(3)cos 6? = cos2( )-sin2( )
= 2cos2( )-1
= 1-2sin2( )
(4)cos25?-sin25?=cos( )2?2?3?3?3?3?10?4?4.公式巩固训练:解:方法一
分别算出tanA,tanB再求tan2A,tan2B,然后求tan(2A+2B)在△ABC中,0
解题过程中要善于发现规律,学会灵活运用.9作业:谢谢指导!1课本P135.1-4
2
