人教新课标B版必修5第二章 数列2.1.1 数列 第一课时课件 20张PPT
文档属性
| 名称 | 人教新课标B版必修5第二章 数列2.1.1 数列 第一课时课件 20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 00:00:00 | ||
图片预览






文档简介
课件20张PPT。2.1数列的概念与简单表示法
(第一课时)1、理解递推公式的含义,能根据递推公式求出数列的前几项。☆ 学习目标2、理解数列的通项公式,对于比较简单的数列,会根据其前几项写出它的一个通项公式。(重点)3、理解数列的几种表示方法,能从函数的观点研究数列。(难点)
① 数列的概念:按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.
集合讲究:无序性、互异性、确定性,数列讲 究:有序性、可重复性、确定性。
② 数列中每一个数叫数列的项,排在第一位的数称为这个数列的第1项(或首项),排在第二位的数称为这个数列的第2项、、、、、、排在第n 位的数称为这个数列的第 n项.
预习准备 熟悉概念③ 数列的一般形式可以写成 ,简记为 .
④ 数列的分类:(1)按项数分:有穷数列与无穷数列,(2)按项之间的大小关系:递增数列、递减数列、常数列与摆动数列.
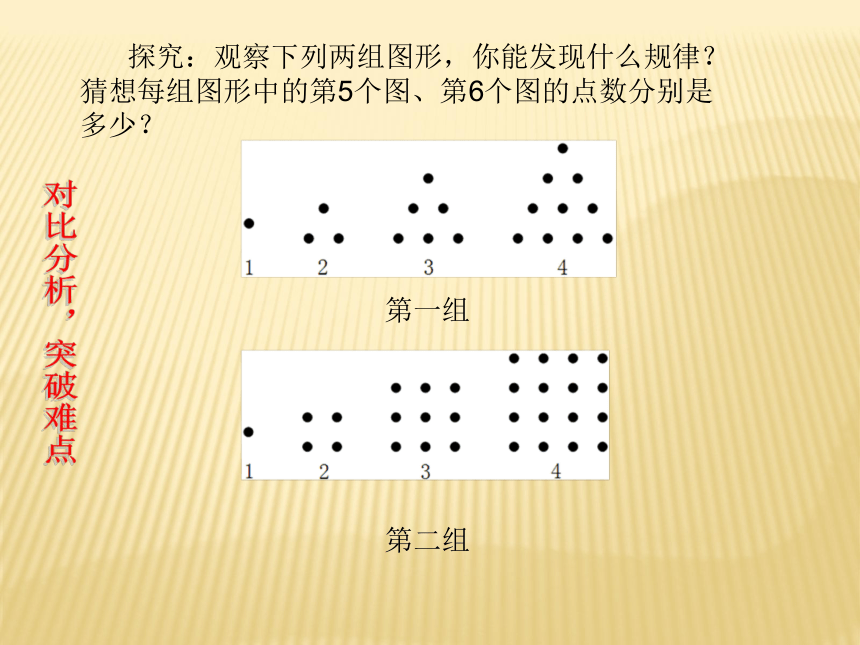
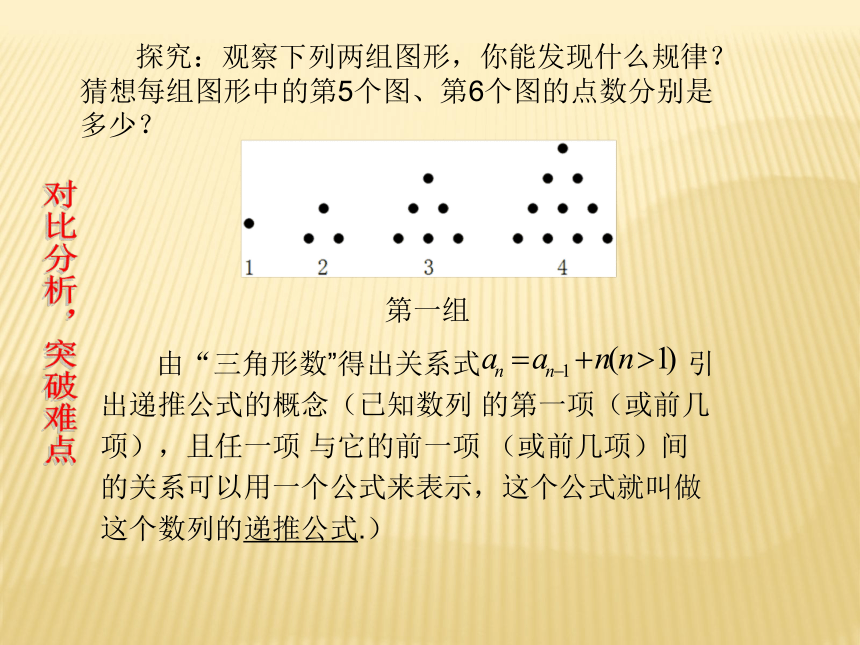
预习准备 熟悉概念 探究:观察下列两组图形,你能发现什么规律?
猜想每组图形中的第5个图、第6个图的点数分别是多少?对比分析,突破难点第一组
第二组 探究:观察下列两组图形,你能发现什么规律?
猜想每组图形中的第5个图、第6个图的点数分别是多少?对比分析,突破难点第一组 由“三角形数”得出关系式 引出递推公式的概念(已知数列 的第一项(或前几项),且任一项 与它的前一项 (或前几项)间的关系可以用一个公式来表示,这个公式就叫做这个数列的递推公式.)
正方形数1,4,9,16,25,36,…,中序号与项的关系 .第二组由“正方形数”得出关系式 得出数列通项公式的概念(如果数列 的第n项与序号n之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式,我们可以根据数列的通项公式写出数列。)
思考:由通项公式你可以得出数列的哪些项呢?任意项对比分析,突破难点讲练结合 运用新知例1:课本P31 例3
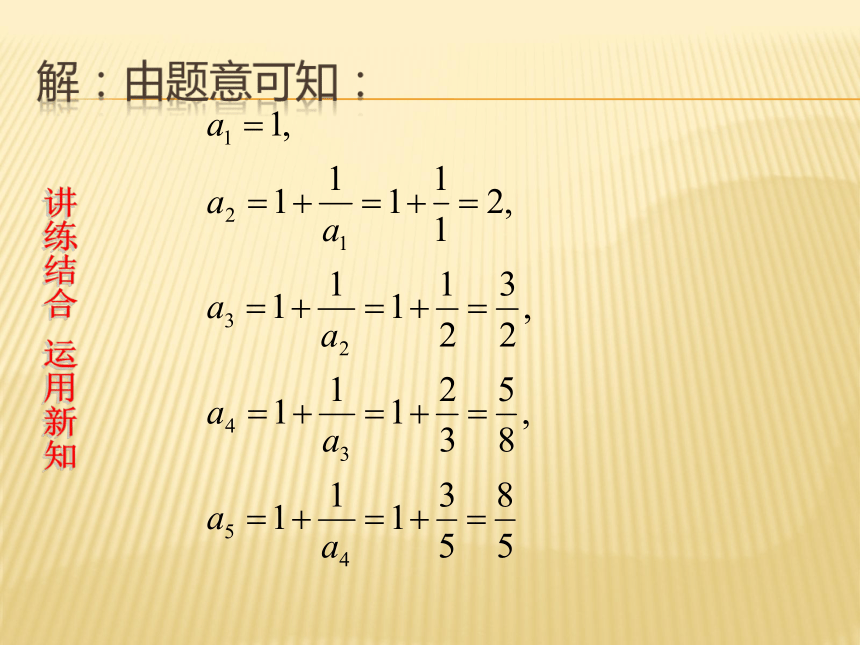
设数列 满足 ,请写出数列的前5项
解:由题意可知:讲练结合 运用新知斐波那契数列,已知写出此数列的前5项。练习1:讲练结合 运用新知例2:写出下面数列的一个通项公式,使它的前4项分别是下列各数:练习2:课本P31 练习题第4题讲练结合 运用新知1.前四项分别是:例3、图中的三角形称为谢宾斯基(Sierpinski)三角形,在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在直角坐标系中画出它的图象。2.此数列的一个通项公式:1 ,3 ,9 ,273. 作图讲练结合 运用新知从例题中我们发现数列有以下表示方法(1) 列表法 (列出序号n与项的对应值)(2) 图象法 (一系列孤立的点)(3) 通项公式法(解析法): 数列的表示方法对比分析,突破难点对比分析 突破难点第一关:观察规律填空(1)( ),-4 ,9 ,( ) ,25,( ),49当堂检测 一站到底1-16-36第二关:4是该数列的第几项? 当堂检测 一站到底4第三关:你能写出这个数列的通项公式吗? 当堂检测 一站到底
9,99,999,9999,……第四关:你能写出这个数列的通项公式吗? 当堂检测 一站到底
1,11,111,1111,……小结归纳 布置作业1、回顾本节学习的数列的几种简单表示法:通项公式、图象法、列表法、递推公式,与函数的表示法进行类比。
2.数学思想方法与学科素养:主要运用类比比较、逻辑推理、抽象概括、数学运算等。布置作业:P33 习题2.1 A组 2、4;B组3题(选作)做作业本上,其余做书上。
谢谢2019年3月15日
① 数列的概念:按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.
集合讲究:无序性、互异性、确定性,数列讲 究:有序性、可重复性、确定性。
② 数列中每一个数叫数列的项,排在第一位的数称为这个数列的第1项(或首项),排在第二位的数称为这个数列的第2项、、、、、、排在第n 位的数称为这个数列的第 n项.
预习准备 熟悉概念③ 数列的一般形式可以写成 ,简记为 .
④ 数列的分类:(1)按项数分:有穷数列与无穷数列,(2)按项之间的大小关系:递增数列、递减数列、常数列与摆动数列.
预习准备 熟悉概念 探究:观察下列两组图形,你能发现什么规律?
猜想每组图形中的第5个图、第6个图的点数分别是多少?对比分析,突破难点第一组
第二组 探究:观察下列两组图形,你能发现什么规律?
猜想每组图形中的第5个图、第6个图的点数分别是多少?对比分析,突破难点第一组 由“三角形数”得出关系式 引出递推公式的概念(已知数列 的第一项(或前几项),且任一项 与它的前一项 (或前几项)间的关系可以用一个公式来表示,这个公式就叫做这个数列的递推公式.)
正方形数1,4,9,16,25,36,…,中序号与项的关系 .第二组由“正方形数”得出关系式 得出数列通项公式的概念(如果数列 的第n项与序号n之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式,我们可以根据数列的通项公式写出数列。)
思考:由通项公式你可以得出数列的哪些项呢?任意项对比分析,突破难点讲练结合 运用新知例1:课本P31 例3
设数列 满足 ,请写出数列的前5项
解:由题意可知:讲练结合 运用新知斐波那契数列,已知写出此数列的前5项。练习1:讲练结合 运用新知例2:写出下面数列的一个通项公式,使它的前4项分别是下列各数:练习2:课本P31 练习题第4题讲练结合 运用新知1.前四项分别是:例3、图中的三角形称为谢宾斯基(Sierpinski)三角形,在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在直角坐标系中画出它的图象。2.此数列的一个通项公式:1 ,3 ,9 ,273. 作图讲练结合 运用新知从例题中我们发现数列有以下表示方法(1) 列表法 (列出序号n与项的对应值)(2) 图象法 (一系列孤立的点)(3) 通项公式法(解析法): 数列的表示方法对比分析,突破难点对比分析 突破难点第一关:观察规律填空(1)( ),-4 ,9 ,( ) ,25,( ),49当堂检测 一站到底1-16-36第二关:4是该数列的第几项? 当堂检测 一站到底4第三关:你能写出这个数列的通项公式吗? 当堂检测 一站到底
9,99,999,9999,……第四关:你能写出这个数列的通项公式吗? 当堂检测 一站到底
1,11,111,1111,……小结归纳 布置作业1、回顾本节学习的数列的几种简单表示法:通项公式、图象法、列表法、递推公式,与函数的表示法进行类比。
2.数学思想方法与学科素养:主要运用类比比较、逻辑推理、抽象概括、数学运算等。布置作业:P33 习题2.1 A组 2、4;B组3题(选作)做作业本上,其余做书上。
谢谢2019年3月15日
