1.2 利用二分法求方程的近似解 课件 22张PPT
文档属性
| 名称 | 1.2 利用二分法求方程的近似解 课件 22张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 16:59:27 | ||
图片预览






文档简介
课件22张PPT。用二分法求方程的近似解高一北师大版
你会解方程吗?? 在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障.这是一条10km长的线路,如何迅速查出故障所在?一、创设情境,引发思考 如果沿着线路一小段一小段查找,困难很多.每查一个点要爬一次电线杆,10km长,大约有200多根电线杆呢.想一想 如果要把故障可能发生的范围缩小到
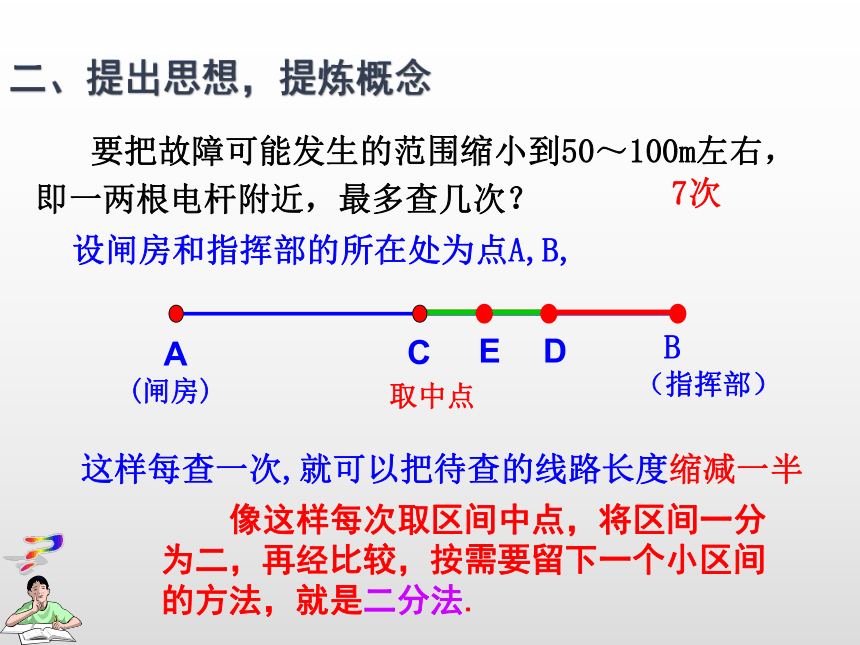
50~100m左右,即一两根电杆附近,最多 查几次? 设闸房和指挥部的所在处为点A,B, 这样每查一次,就可以把待查的线路长度缩减一半 要把故障可能发生的范围缩小到50~100m左右,即一两根电杆附近,最多查几次? 7次取中点 像这样每次取区间中点,将区间一分为二,再经比较,按需要留下一个小区间的方法,就是二分法.二、提出思想,提炼概念设闸房和指挥部的所在处为点A,B,取中点1.故障点在AB之间;
2.取中点,通电检测,故障点在不通电的一半线路;
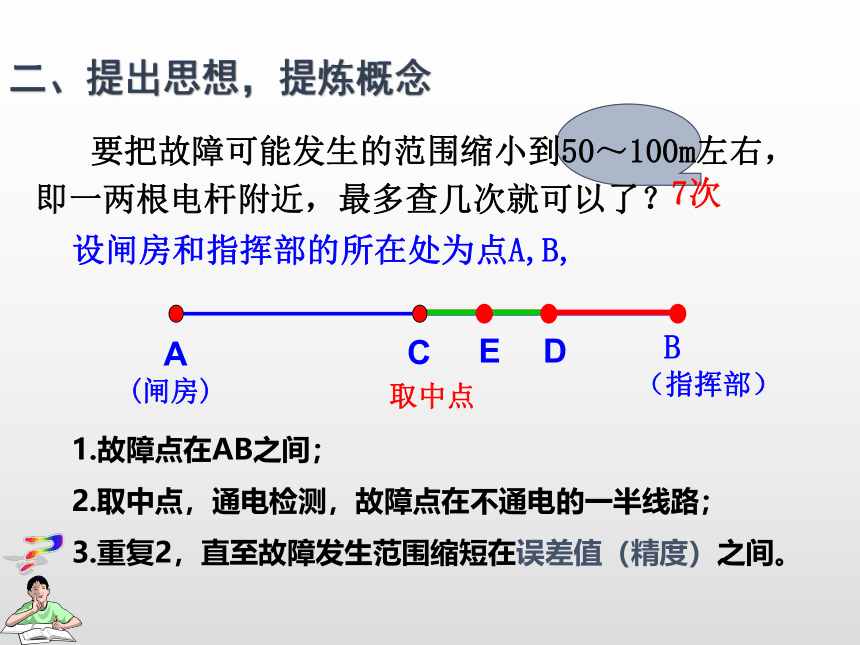
3.重复2,直至故障发生范围缩短在误差值(精度)之间。 要把故障可能发生的范围缩小到50~100m左右,即一两根电杆附近,最多查几次就可以了? 7次二、提出思想,提炼概念例:求方程 的近似解.
(精度为0.1)三、利用概念,解决问题1.故障点在AB之间;
2.取中点,通电检测,故障点在不通电的一半线路;
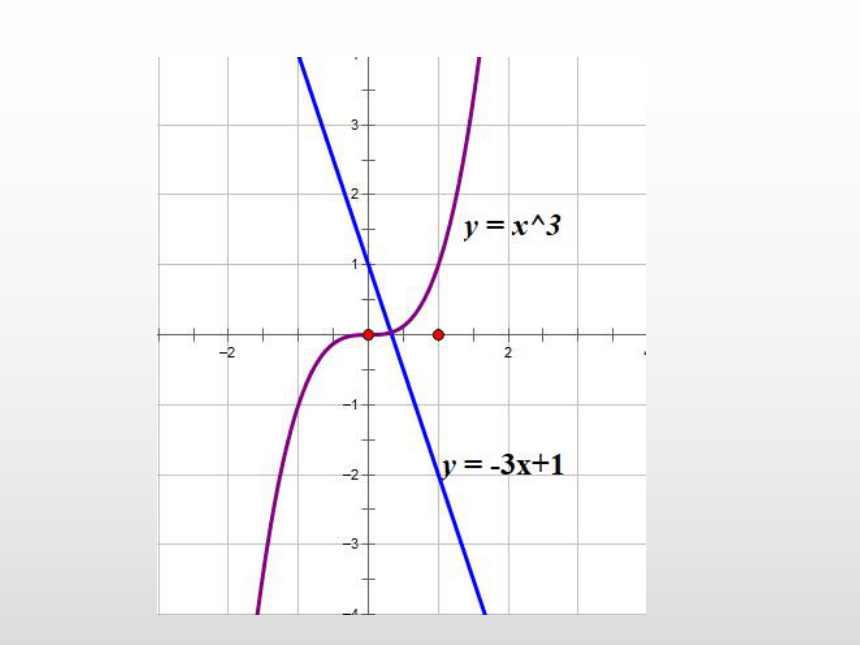
3.重复2,直至故障发生范围缩短在误差值(精度)之间。分析:求函数 的零点。例:求方程 的近似解.
(精度为0.1)1.确定零点所在区间;
2.取中点,通电检测,故障点在不通电的一半线路;
3.重复2,直至故障发生范围缩短在误差值(精度)之间。分析:求函数 的零点。零点存在性定理!三、利用概念,解决问题例:求方程 的近似解.
(误差不超过0.1)1.确定零点所在区间;
2.取中点,通电检测,故障点在不通电的一半线路;
3.重复2,直至故障发生范围缩短在误差值(精度)之间。分析:求函数 的零点。零点存在性定理!三、利用概念,解决问题例:求方程 的近似解.
(误差不超过0.1)1.确定零点所在区间;
2.取中点,则零点在满足“零点存在性定理”的一半区间内;
3.重复2,直至故障发生范围缩短在误差值(精度)之间。分析:求函数 的零点。零点存在性定理!三、利用概念,解决问题例:求方程 的近似解(精度为0.1).1.确定零点所在区间;
2.取中点,则零点在满足“零点存在性定理”的一半区间内;
3.重复2,直至所求区间满足精度要求(误差不超过0.1)。分析:求函数 的零点。零点存在性定理!三、利用概念,解决问题 精度为0.1,即零点值与近似值的差的绝对值要小于或等于0.1。求函数 的零点:已知函数 在区间
内有零点,求出此零点的近似值(精度为0.1) 合作探究:f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75f(2.75)>0f(2.5)<0,
f(2.75)>02.625f(2.625)>0(2.5, 2.625)f(2.5)<0, f(2.625)>02.5625f(2.5625)>0(2.5, 3)(2.5, 2.75)(2.5, 2.5625)四、抽象概括,总结方法总结用二分法求方程近似解的步骤:2.求区间(a,b)的中点c.(1)若 ,则c就是函数的零点.(2)若 ,则零点在(a,c)内.(3)若 ,则零点在(c,b)内.即若满足精度要求,则得到零点近似值;若不满足精度要求,则重复步骤2~4.选区间逼近解确定解定区间,找中点,中值计算两边看.
同号去,异号算,零点落在异号间.
周而复始怎么办? 精度要求来判断.口 诀1. 下列函数的图象与x轴均有交点,其中不能用
二分法求其零点的是( )五、当堂检测,学以致用2.某同学在借助计算器求“方程 的近似解
(精度0.1)”时,设 , 算得
;在以下过程中,他用“二分法”又
取了4个x的值,计算了其函数值的正负,并得出判
断:方程的近似解是 .那么他所取的x的4个值
中最后一个值是________.1.812 5五、当堂检测,学以致用1.二分法的定义.
2.用二分法求方程近似解(即函数零点近 似值)的步骤.
3.逐步逼近思想.
4.数形结合思想.
5.近似与精确的相对统一. 六、课堂小结,作业布置高陵区第一中学录制
2019年5月
50~100m左右,即一两根电杆附近,最多 查几次? 设闸房和指挥部的所在处为点A,B, 这样每查一次,就可以把待查的线路长度缩减一半 要把故障可能发生的范围缩小到50~100m左右,即一两根电杆附近,最多查几次? 7次取中点 像这样每次取区间中点,将区间一分为二,再经比较,按需要留下一个小区间的方法,就是二分法.二、提出思想,提炼概念设闸房和指挥部的所在处为点A,B,取中点1.故障点在AB之间;
2.取中点,通电检测,故障点在不通电的一半线路;
3.重复2,直至故障发生范围缩短在误差值(精度)之间。 要把故障可能发生的范围缩小到50~100m左右,即一两根电杆附近,最多查几次就可以了? 7次二、提出思想,提炼概念例:求方程 的近似解.
(精度为0.1)三、利用概念,解决问题1.故障点在AB之间;
2.取中点,通电检测,故障点在不通电的一半线路;
3.重复2,直至故障发生范围缩短在误差值(精度)之间。分析:求函数 的零点。例:求方程 的近似解.
(精度为0.1)1.确定零点所在区间;
2.取中点,通电检测,故障点在不通电的一半线路;
3.重复2,直至故障发生范围缩短在误差值(精度)之间。分析:求函数 的零点。零点存在性定理!三、利用概念,解决问题例:求方程 的近似解.
(误差不超过0.1)1.确定零点所在区间;
2.取中点,通电检测,故障点在不通电的一半线路;
3.重复2,直至故障发生范围缩短在误差值(精度)之间。分析:求函数 的零点。零点存在性定理!三、利用概念,解决问题例:求方程 的近似解.
(误差不超过0.1)1.确定零点所在区间;
2.取中点,则零点在满足“零点存在性定理”的一半区间内;
3.重复2,直至故障发生范围缩短在误差值(精度)之间。分析:求函数 的零点。零点存在性定理!三、利用概念,解决问题例:求方程 的近似解(精度为0.1).1.确定零点所在区间;
2.取中点,则零点在满足“零点存在性定理”的一半区间内;
3.重复2,直至所求区间满足精度要求(误差不超过0.1)。分析:求函数 的零点。零点存在性定理!三、利用概念,解决问题 精度为0.1,即零点值与近似值的差的绝对值要小于或等于0.1。求函数 的零点:已知函数 在区间
内有零点,求出此零点的近似值(精度为0.1) 合作探究:f(2)<0, f(3)>02.5f(2.5)<0f(2.5)<0, f(3)>02.75f(2.75)>0f(2.5)<0,
f(2.75)>02.625f(2.625)>0(2.5, 2.625)f(2.5)<0, f(2.625)>02.5625f(2.5625)>0(2.5, 3)(2.5, 2.75)(2.5, 2.5625)四、抽象概括,总结方法总结用二分法求方程近似解的步骤:2.求区间(a,b)的中点c.(1)若 ,则c就是函数的零点.(2)若 ,则零点在(a,c)内.(3)若 ,则零点在(c,b)内.即若满足精度要求,则得到零点近似值;若不满足精度要求,则重复步骤2~4.选区间逼近解确定解定区间,找中点,中值计算两边看.
同号去,异号算,零点落在异号间.
周而复始怎么办? 精度要求来判断.口 诀1. 下列函数的图象与x轴均有交点,其中不能用
二分法求其零点的是( )五、当堂检测,学以致用2.某同学在借助计算器求“方程 的近似解
(精度0.1)”时,设 , 算得
;在以下过程中,他用“二分法”又
取了4个x的值,计算了其函数值的正负,并得出判
断:方程的近似解是 .那么他所取的x的4个值
中最后一个值是________.1.812 5五、当堂检测,学以致用1.二分法的定义.
2.用二分法求方程近似解(即函数零点近 似值)的步骤.
3.逐步逼近思想.
4.数形结合思想.
5.近似与精确的相对统一. 六、课堂小结,作业布置高陵区第一中学录制
2019年5月
