2.1 函数概念 课件 28张PPT
图片预览





文档简介
课件28张PPT。1.2.1 函数的概念“函”,
原意匣。1673年,德国数学家莱布尼兹首次使用“fun_ction”(函数)一词,后又经康托尔在集合论的基础上,揭示了函数的本质,中国清代数学家李善兰1859年在翻译《代数学》一书时,将fun_ction翻译成函数,将函数一词引入中国,他翻译到凡式中含天,为天之函数。函数初现李善兰
1811-1882
清朝数学家莱布尼兹
1646-1716
德国数学家1673-1859 康托尔 ( Cantor )
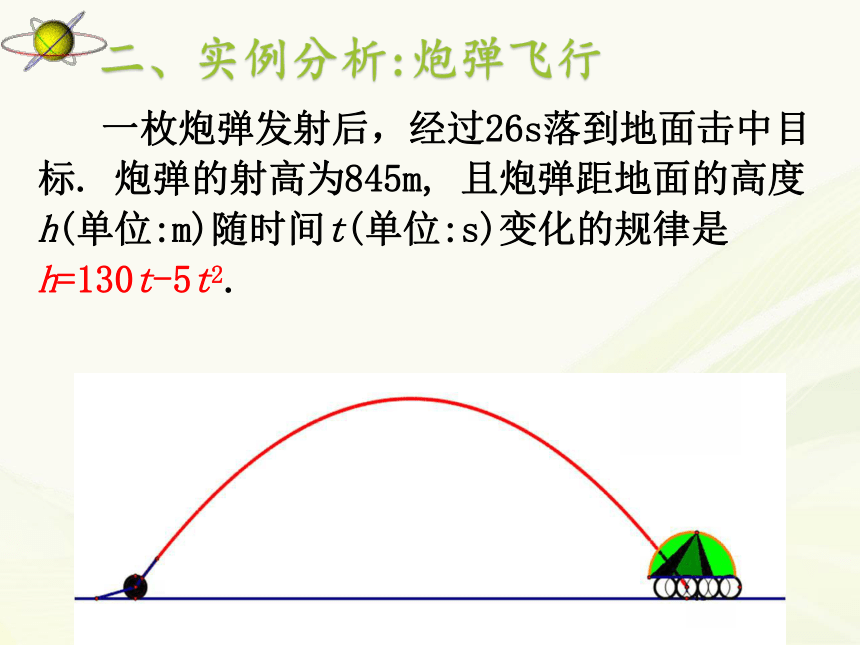
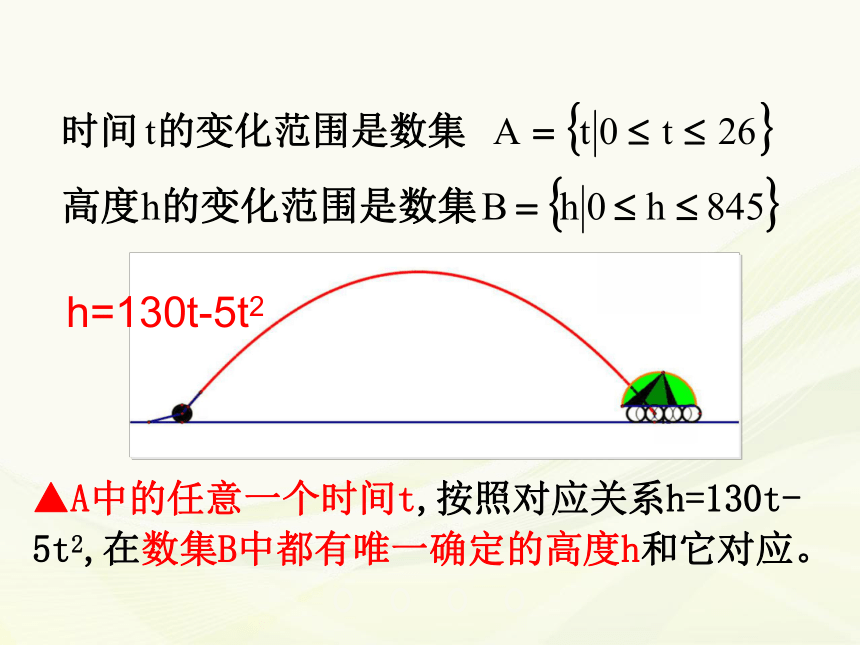
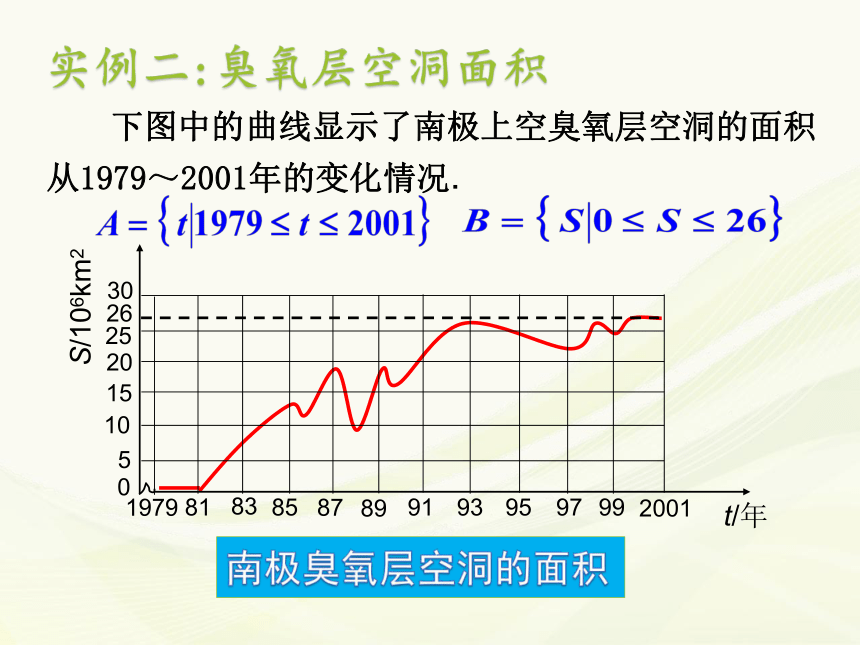
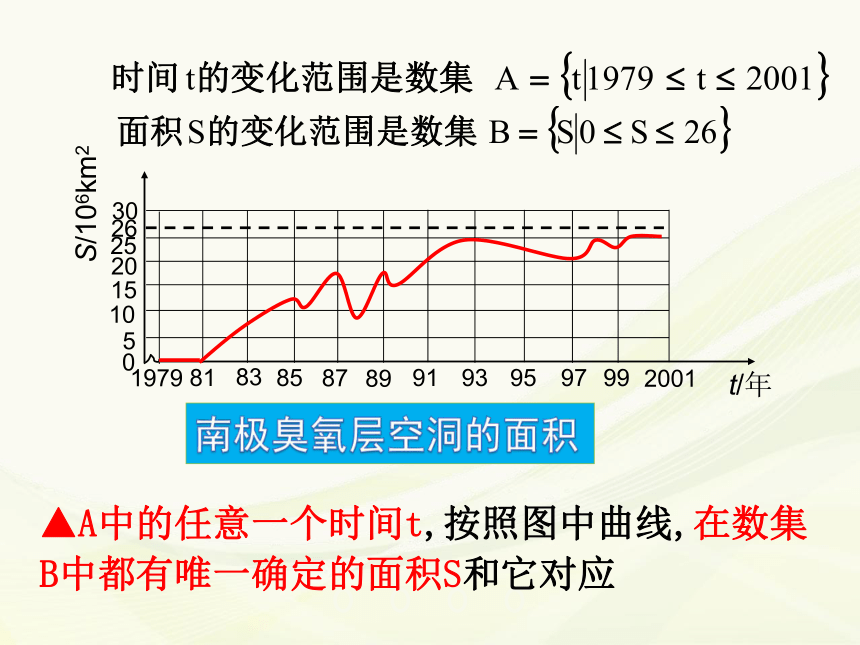
(德,1845--1918)初中阶段我们都学过哪些函数呢??x0x0x0x0y0y0y0y0一、知识回顾: 初中学习的函数的定义是什么?一、知识回顾: 一般地,在一个变化过程中有两个变量x和y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说y是x的函数.其中x叫自变量,y叫因变量. 一枚炮弹发射后,经过26s落到地面击中目标. 炮弹的射高为845m, 且炮弹距地面的高度h(单位:m)随时间t(单位:s)变化的规律是h=130t-5t2.二、实例分析:炮弹飞行 h=130t-5t2▲A中的任意一个时间t,按照对应关系h=130t-5t2,在数集B中都有唯一确定的高度h和它对应。 下图中的曲线显示了南极上空臭氧层空洞的面积从1979~2001年的变化情况.实例二:臭氧层空洞面积南极臭氧层空洞的面积 ▲A中的任意一个时间t,按照图中曲线,在数集B中都有唯一确定的面积S和它对应
“八五”计划以来我国城镇居民恩格尔系数变化情况仿照实例(1)(2),试描述上表中恩格尔系数和时间(年)的关系.A={1991,1992,1993,1994,1995,1996,1997,1998,1999,2000,2001}B={53.8, 52.9, 50.1, 49.9, 48.6, 46.4, 44.5, 41.9, 39.2, 37.9}实例三:恩格尔系数▲A中的任意一个时间t,按照表格,在数集B中都有唯一确定的系数和它对应。以上三个实例中变量的对应关系有什么共同点呢?不同点呢?(2)两个数集间都有一种确定的对应关系;(3)对于数集A中的任意一个数,数集B中
都有唯一确定的数和它对应.(1)都有两个非空数集A,B;记作:三、归纳概括 你能用集合与对应的语言
来刻画函数,抽象概括出函数
的概念吗? 小组合作探究 设A,B是非空的数集,如果按照某种
确定的对应关系f,使对于集合A中的任意
一个数,在集合B中都有唯一确定的数f(x)
和它对应,那么称 为从集合A
到集合B的一个函数.记作 . 其中,x叫做自变量,集合A叫做函数的定义域. 与x的值对应的y值叫做函数值,函数值的集合 叫做函数的值域.
自变量的取值范围A叫做函数的定义域; 函数值的集合{f(x)|x∈A}叫做函数的值域.例如:定义域为{0,1,2},值域为{0,2,4} 函数的概念既已形成,那么它的本质是什么呢?我们先看一个表格,请学号01-05的同学填写上次考试的数学成绩,之后回答下面3个问题: 问题1:若学号构成集合A={01,02,03,04,05},成绩构成集合 B={132,135,120,125,122},f:上次考试数学成绩,由A到B能否构成函数? 问题2:若将问题1中集合A改为“A={杜杭,王丽,林晨晨,姚壮 ,田汶帅}”,其余条件不变,那么由A到B能否构成函数? 问题3:若学号04的学生上次考试因病缺考,无成绩,那么学号与成绩能否构成函数?【概念辨析】AB(1)(2)(3)乘2平方求倒数AABB(1)如何判断给定的两个变量间是否具有函数关系
①必须有两个非空数集
② f:A→B表示从A到B的函数(具有方向性,同B到A不一样),对应的特点:A无余,B可余,可以一对一、多对一,但不能一对多.
(2)如何理解y=f(x)?
y=f(x)表示“ y是变量x的函数”,它仅仅是函数符号,并不表示y等于f与x的乘积。f(x)与f(a)(a是常数)的区别联系: f(a)表示x=a时的函数值,f(x)是自变量x的函数.
(3)f表示对应关系,也可用g、F、G…等均可.
(4)函数的三要素:定义域、值域、对应关系f缺一不可.
(5)相同的函数:定义域、对应关系都相同的函数.
函数概念的理解四、例题辨析:1.已知数集A={1,2,3,4},数集B={2,4,6} ,那 么f(x)=2x是不是从数集A到数集B的函数?ABfABfABfABfABf(1)(2)(3)(4)(5)否否是是是2.否1.下列可作为函数y= f (x)的图象的是( ) A B C DxxxxyyyyOOOO√练习反馈2.判断下列对应能否表示y是x的函数(1) y=|x| (2)|y|=x
(3) y=x 2 (4)y2 =x
(5) y2+x2=1 (6)y2-x2=1 (1)能 (2)不能 (5)不能 (3)能 (4)不能 (6)不能 3.给出四个命题:
①定义域相同,值域相同的两个函数相等。
②若函数的定义域只含有一个元素,则值域也只有一个元素
③因f(x)=5(x∈R),这个函数值不随x的变化范围而变化,所以f(0)=5也成立
④定义域和对应关系确定后,函数值也就确定了 正确有( )
A、1个 B、2个 C、3个 D、4个C实数集R 使分母不等于0的实数x的集合使根号内的式子大于或等于0的实数x的集合实数集R使实际问题有意义的实数x的集合 例2:求下列函数的定义域: 3.一个函数的构成要素:定义域对应关系值域决定 定义域
对应关系完全一致函数相等例3:下列函数中哪个与函数y=x相等练习:下列各组中的两个函数是否为相同的函数?(1)定义域不同。
(2)定义域不同。
(3)定义域和值域都不同。知识:1.判断两个变量是否有函数关系;
2.定义域求法3.判断是否为相同函数
方法:①函数问题首先考虑定义域;②f(x)含对x的一种操作规定,不是f与x的乘积③f(a)表示当x=a时数f(x)的函数值;④注意分类讨论思想的应用。
作业:(必做)教材P28练习1,2 (选做)P34A组1 小结:
谢谢聆听!
原意匣。1673年,德国数学家莱布尼兹首次使用“fun_ction”(函数)一词,后又经康托尔在集合论的基础上,揭示了函数的本质,中国清代数学家李善兰1859年在翻译《代数学》一书时,将fun_ction翻译成函数,将函数一词引入中国,他翻译到凡式中含天,为天之函数。函数初现李善兰
1811-1882
清朝数学家莱布尼兹
1646-1716
德国数学家1673-1859 康托尔 ( Cantor )
(德,1845--1918)初中阶段我们都学过哪些函数呢??x0x0x0x0y0y0y0y0一、知识回顾: 初中学习的函数的定义是什么?一、知识回顾: 一般地,在一个变化过程中有两个变量x和y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说y是x的函数.其中x叫自变量,y叫因变量. 一枚炮弹发射后,经过26s落到地面击中目标. 炮弹的射高为845m, 且炮弹距地面的高度h(单位:m)随时间t(单位:s)变化的规律是h=130t-5t2.二、实例分析:炮弹飞行 h=130t-5t2▲A中的任意一个时间t,按照对应关系h=130t-5t2,在数集B中都有唯一确定的高度h和它对应。 下图中的曲线显示了南极上空臭氧层空洞的面积从1979~2001年的变化情况.实例二:臭氧层空洞面积南极臭氧层空洞的面积 ▲A中的任意一个时间t,按照图中曲线,在数集B中都有唯一确定的面积S和它对应
“八五”计划以来我国城镇居民恩格尔系数变化情况仿照实例(1)(2),试描述上表中恩格尔系数和时间(年)的关系.A={1991,1992,1993,1994,1995,1996,1997,1998,1999,2000,2001}B={53.8, 52.9, 50.1, 49.9, 48.6, 46.4, 44.5, 41.9, 39.2, 37.9}实例三:恩格尔系数▲A中的任意一个时间t,按照表格,在数集B中都有唯一确定的系数和它对应。以上三个实例中变量的对应关系有什么共同点呢?不同点呢?(2)两个数集间都有一种确定的对应关系;(3)对于数集A中的任意一个数,数集B中
都有唯一确定的数和它对应.(1)都有两个非空数集A,B;记作:三、归纳概括 你能用集合与对应的语言
来刻画函数,抽象概括出函数
的概念吗? 小组合作探究 设A,B是非空的数集,如果按照某种
确定的对应关系f,使对于集合A中的任意
一个数,在集合B中都有唯一确定的数f(x)
和它对应,那么称 为从集合A
到集合B的一个函数.记作 . 其中,x叫做自变量,集合A叫做函数的定义域. 与x的值对应的y值叫做函数值,函数值的集合 叫做函数的值域.
自变量的取值范围A叫做函数的定义域; 函数值的集合{f(x)|x∈A}叫做函数的值域.例如:定义域为{0,1,2},值域为{0,2,4} 函数的概念既已形成,那么它的本质是什么呢?我们先看一个表格,请学号01-05的同学填写上次考试的数学成绩,之后回答下面3个问题: 问题1:若学号构成集合A={01,02,03,04,05},成绩构成集合 B={132,135,120,125,122},f:上次考试数学成绩,由A到B能否构成函数? 问题2:若将问题1中集合A改为“A={杜杭,王丽,林晨晨,姚壮 ,田汶帅}”,其余条件不变,那么由A到B能否构成函数? 问题3:若学号04的学生上次考试因病缺考,无成绩,那么学号与成绩能否构成函数?【概念辨析】AB(1)(2)(3)乘2平方求倒数AABB(1)如何判断给定的两个变量间是否具有函数关系
①必须有两个非空数集
② f:A→B表示从A到B的函数(具有方向性,同B到A不一样),对应的特点:A无余,B可余,可以一对一、多对一,但不能一对多.
(2)如何理解y=f(x)?
y=f(x)表示“ y是变量x的函数”,它仅仅是函数符号,并不表示y等于f与x的乘积。f(x)与f(a)(a是常数)的区别联系: f(a)表示x=a时的函数值,f(x)是自变量x的函数.
(3)f表示对应关系,也可用g、F、G…等均可.
(4)函数的三要素:定义域、值域、对应关系f缺一不可.
(5)相同的函数:定义域、对应关系都相同的函数.
函数概念的理解四、例题辨析:1.已知数集A={1,2,3,4},数集B={2,4,6} ,那 么f(x)=2x是不是从数集A到数集B的函数?ABfABfABfABfABf(1)(2)(3)(4)(5)否否是是是2.否1.下列可作为函数y= f (x)的图象的是( ) A B C DxxxxyyyyOOOO√练习反馈2.判断下列对应能否表示y是x的函数(1) y=|x| (2)|y|=x
(3) y=x 2 (4)y2 =x
(5) y2+x2=1 (6)y2-x2=1 (1)能 (2)不能 (5)不能 (3)能 (4)不能 (6)不能 3.给出四个命题:
①定义域相同,值域相同的两个函数相等。
②若函数的定义域只含有一个元素,则值域也只有一个元素
③因f(x)=5(x∈R),这个函数值不随x的变化范围而变化,所以f(0)=5也成立
④定义域和对应关系确定后,函数值也就确定了 正确有( )
A、1个 B、2个 C、3个 D、4个C实数集R 使分母不等于0的实数x的集合使根号内的式子大于或等于0的实数x的集合实数集R使实际问题有意义的实数x的集合 例2:求下列函数的定义域: 3.一个函数的构成要素:定义域对应关系值域决定 定义域
对应关系完全一致函数相等例3:下列函数中哪个与函数y=x相等练习:下列各组中的两个函数是否为相同的函数?(1)定义域不同。
(2)定义域不同。
(3)定义域和值域都不同。知识:1.判断两个变量是否有函数关系;
2.定义域求法3.判断是否为相同函数
方法:①函数问题首先考虑定义域;②f(x)含对x的一种操作规定,不是f与x的乘积③f(a)表示当x=a时数f(x)的函数值;④注意分类讨论思想的应用。
作业:(必做)教材P28练习1,2 (选做)P34A组1 小结:
谢谢聆听!
