3.1 函数的单调性:20张PPT

课件20张PPT。 1.3.1
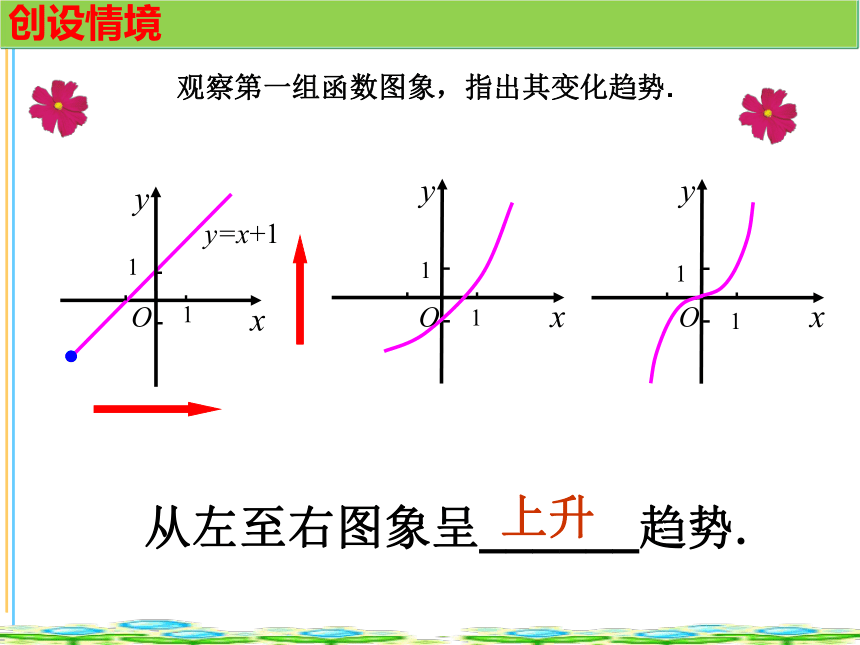
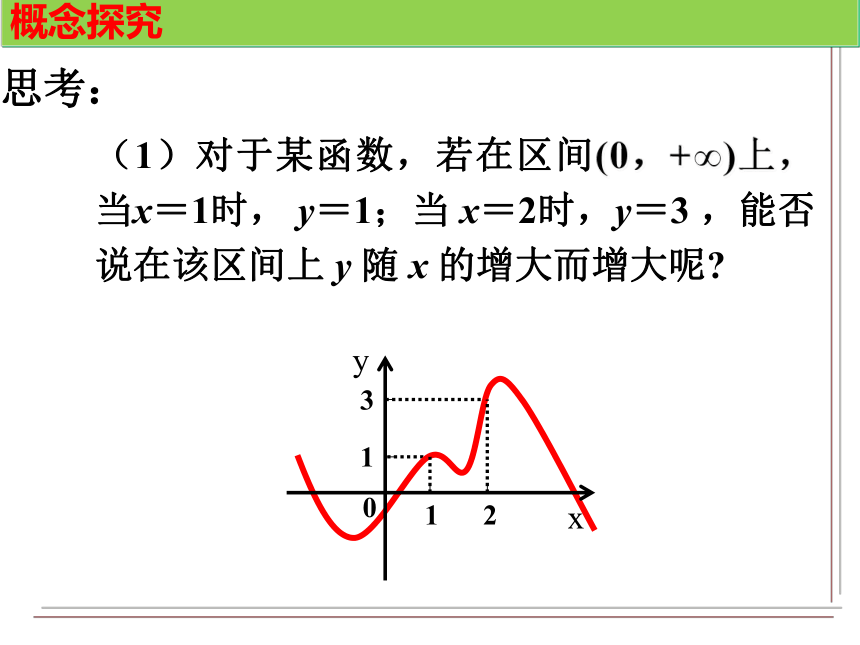
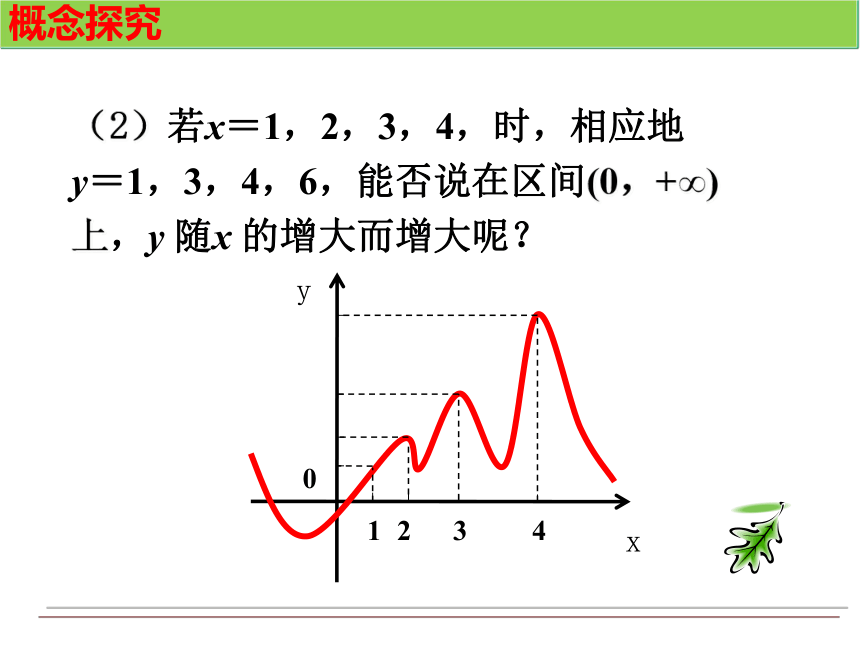
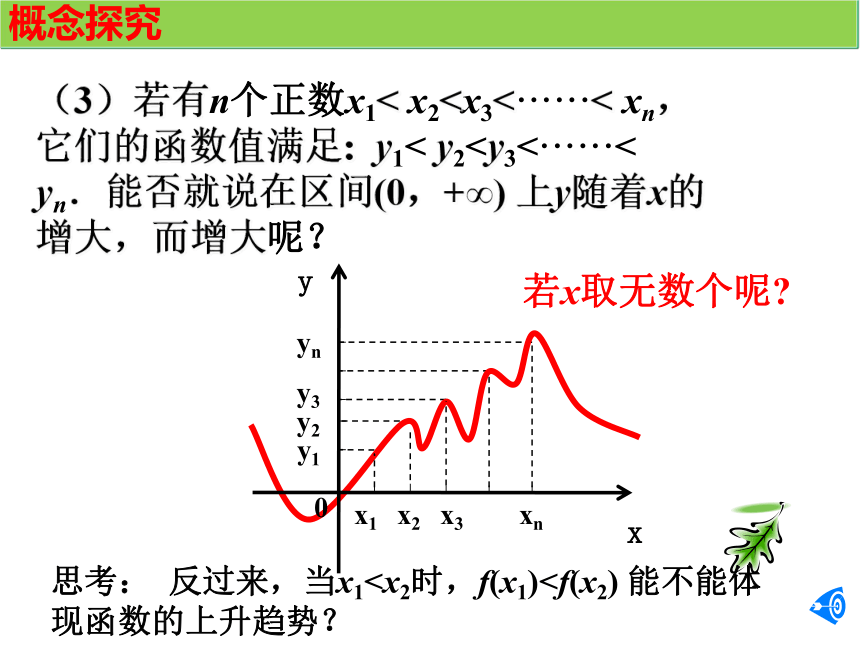
函 数 的 单 调 性北师大版必修一第二章第三节创设情境从左至右图象呈______趋势.上升观察第一组函数图象，指出其变化趋势.OOO111111创设情境从左至右图象呈______趋势.下降观察第二组函数图象，指出其变化趋势.OOO111111创设情境y从左至右图象呈______________趋势.局部上升或下降　　　　观察第三组函数图象，指出其变化趋势.xy11-1-1OOO1111创设情境“x逐渐增大”x1 ＜ x2“x逐渐增大，函数值f(x)也增大”“函数值f(x)也增大f(x1)＜f(x2)当 x1＜x2 时，都有f(x1)＜f(x2)概念探究在x ∈[0,+∞)上：思考： 反过来，当x1 （1）对于某函数，若在区间(0，+∞)上，当x＝1时， y＝1；当 x＝2时，y＝3 ，能否说在该区间上 y 随 x 的增大而增大呢?思考：概念探究（2）若x＝1，2，3，4，时，相应地 y＝1，3，4，6，能否说在区间(0，+∞)上，y 随x 的增大而增大呢？概念探究（3）若有n个正数x1< x2 概念形成函数f (x)在给定区间上为增函数。如何用x与 f(x)来描述下降的图象？函数f (x)在给定区间上为减函数。概念形成如果函数 y=f(x) 在某个区间是增函数或是减函数，那么就是说函数 y=f(x) 在这个区间具有(严格的)单调性，这一区间叫做单调区间，其中是增函数的区间叫增区间；为减函数的叫减区间。“或”字表示在该区间上要么是增函数，要么是减函数，两者只能为其一函数单调性和单调区间的概念：典例分析例1 下图是定义在闭区间[-5,5]上的函
数 的图象,根据图象说出
的单调区间,以及在每一区间上,
是增函数还是减函数.作图是发现函数单调性的方法之一.典例分析例2：证明函数f(x)=3x+2在R上是增函数。证明：任意取 , ,且因为所以函数f(x)=3x+2在R上是增函数取值作差变形判断符号下结论练习1.画出下列函数图像，并写出单调区间：巩固深化
练习1：填表函数单调区间k >0k <0k >0k <0增函数减函数减函数增函数单调性巩固深化练习2.画出下列函数图像，并写出单调区间：巩固深化变式：讨论的单调性函数单调区间单调性增函数增函数练习2：填表（二）减函数减函数巩固深化增函数练习：求证函数 　　　　 在区间
［－1，＋∞）上是单调减函数． 取值作差变形判号下结论巩固深化增函数和减函数的定义函数单调性、单调区间的概念回顾总结谈谈你的收获判断函数单调性的两种方法图像法、定义法数学思想方法：数形结合特殊到一般对比知识点：作业巩固作业：P39 第1、2题