3.1.2 指数函数 课件 36张PPT
文档属性
| 名称 | 3.1.2 指数函数 课件 36张PPT |
|
|
| 格式 | zip | ||
| 文件大小 | 865.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 00:00:00 | ||
图片预览








文档简介
课件36张PPT。
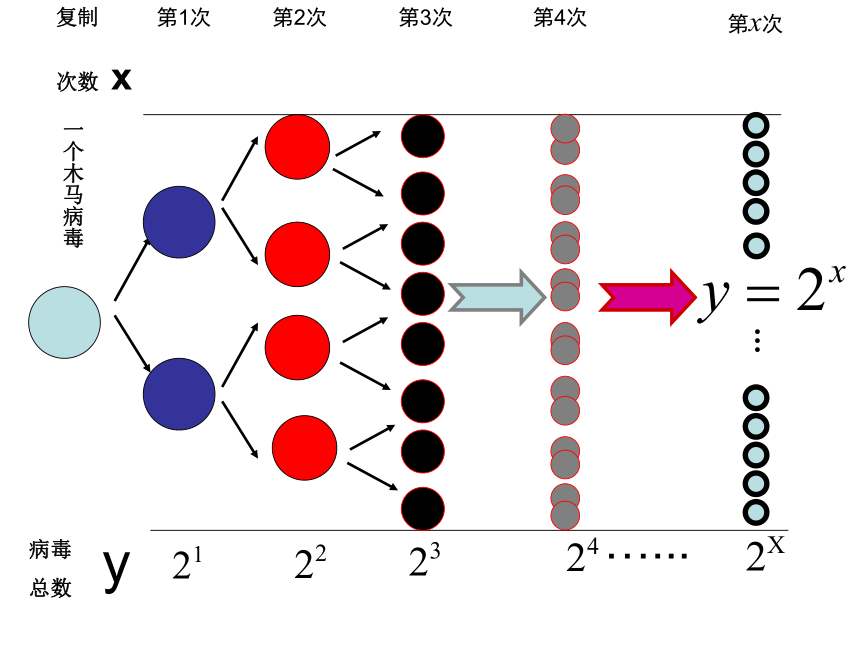
3.1.2 指数函数
学习目标1、了解指数函数模型的实际背景;
2、理解指数函数的概念、图像和性质。
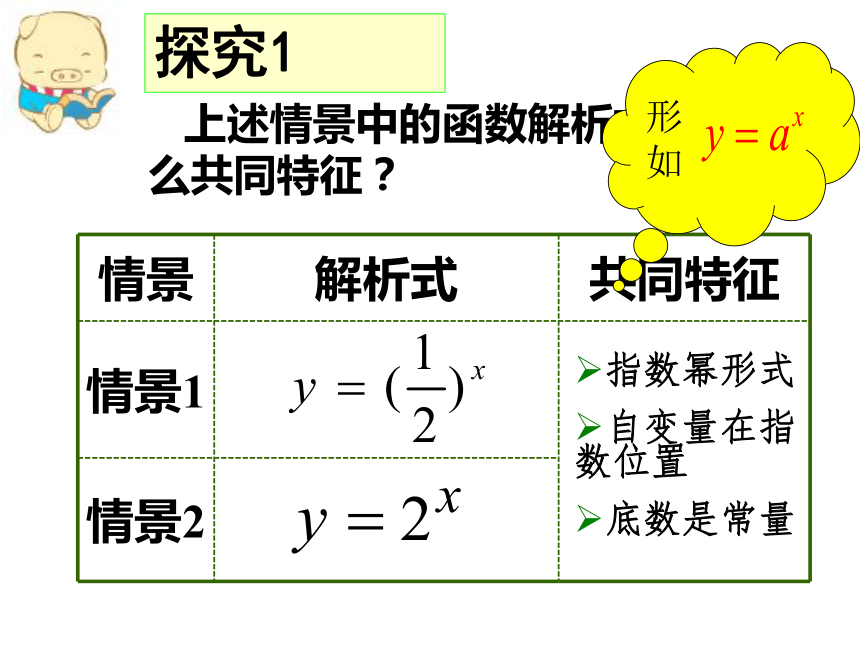
指数函数的性质和应用。 重点难点指数函数的概念和性质。……情景1:一把长为1的尺子第一次截去它的一半,第二次截去剩余部分的一半,第三次截去第二次剩余部分的一半,依次截下去,问截的次数x与剩下的尺子长度y之间的关系.情景2:“ 木马病毒”被认为是破坏性极强的计算机病毒之一,具有快速自我复制能力,它可以由1个变成2个,2个变成4个……复制x次后,你知道所得病毒个数y与x的函数关系式是什么?复制
次数 x第1次第2次第3次第4次…...第x次 上述情景中的函数解析式有什么共同特征?2探究1指数幂形式
自变量在指数位置
底数是常量一、指数函数的定义 一般地,函数 y=a x(a>0 且 a ≠ 1,x ? R )叫做指数函数.其中 x 是自变量,定义域为 R.系数为1底数为大于0且
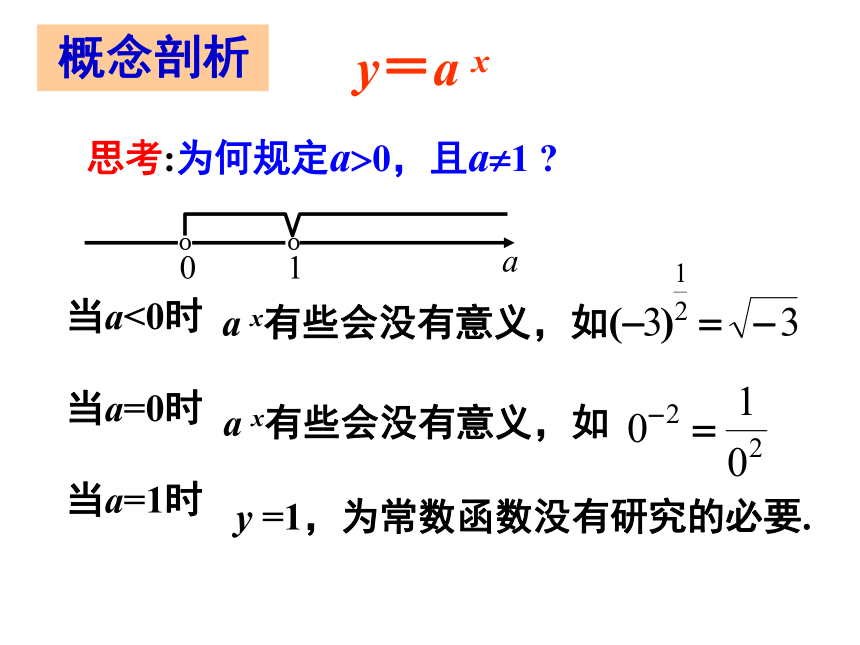
不为1的常数自变量为纯“x”,系数为1 概念剖析y =1,为常数函数没有研究的必要.思考:为何规定a?0,且a?1 ?a x有些会没有意义,如 a x有些会没有意义,如 y=a x当a<0时
当a=0时
当a=1时
例 指出下列函数哪些是指数函数:(1)y=(-3)x; (2) y=?x ;(3)y=0.7x; (4) y=x3.
(口答)判断下列函数是不是指 数函数,为什么?√√函数y=(a2-3a+3)ax是指数函数,求a的值.∴a=2011…0.0370.11
0.33
13927…
y=3-x…2793
10.330.110.037…
y=3x…321
0
-1
-2
-3
…
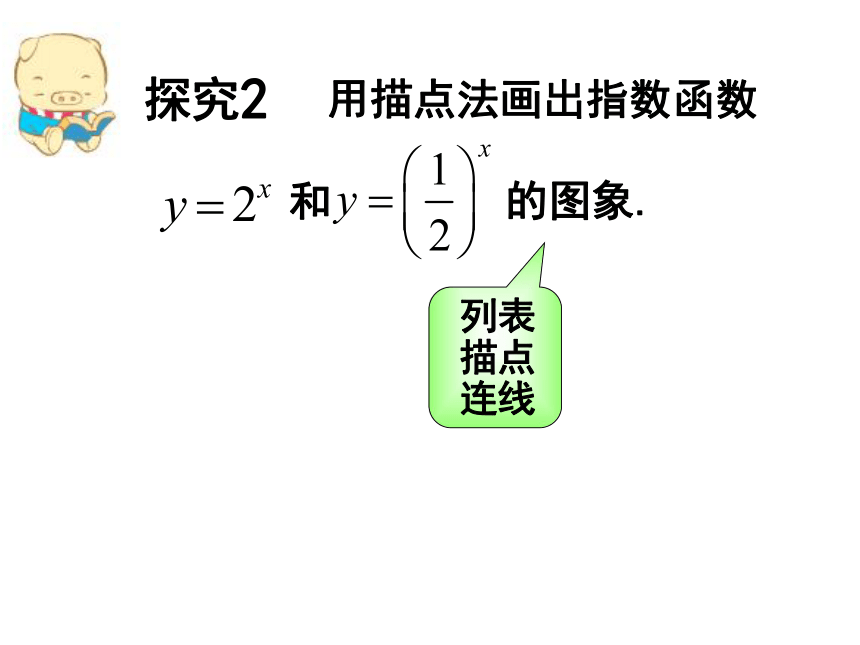
x(2) 与 的图象. 列表:关于y轴对称不是y=ax (01)0101 图象共同特征:(1)图象可向左、右两方无限伸展(3)都经过坐标为(0,1)的点(2)图象都在x轴上方图象自左至右逐渐上升图象自左至右逐渐下降
R( 0 , + ∞)过定点 ( 0 , 1 ) 在R上是增函数在R上是减函数 定义域 值域 定点 单调性a > 10 < a < 1二、指数函数的图象和性质 指函图象半个八,
大一撇来小一捺,
图象必过(0,1)点,?
X轴上方为指家.? 例 用指数函数的性质,判断下列各
函数的单调性:解:(1)因为3>1, 例 比较下列各题中两个值的大小1.72.5与1.73
解:(1) 考虑指数函数 y=1.7x,它是增函数.∵2.5<3 ∴1.72.5<1.73.例 比较下列各题中两个值的大小 :1.72.5与1.73
解:(1) 考虑指数函数 y=1.7x它是增函数.∵2.5<3
∴1.72.5<1.73(2) 1.2与 5解:(2)考虑指数函数它是 .∵练习:比较100.2与1的大小.减函数1.2< 5∴底不同,指数也不同 利用函数图象或中间量进行比较底数相同,但需要分情况讨论 解:①②比较指数大小的方法①同底不同指:对于底数相同,指数不同的两个幂的大小比较,可以构造函数,利用函数的单调性,若底数是参变量要注意分类讨论。②不同底不同指:对于底数不同,指数不同的两个幂的大小比较用别的数如0或1做桥。③同指不同底:对于指数相同,底数不同的两个幂比较大小,可先构造函数,再利用指数函数图象变化规律来判断第一象限中,底大图高-1第二象限中,底大图低1、底数互为倒数的两个指数函数图像关于y轴对称2、 当a>1时, 底数越大,图像越陡
当 04、指数函数图像的相对位置于底数大小的关系:
(1)y轴右侧,图像从下到上相应底数由小变大底大图高;
(2)Y轴左侧,图像从上到下相应底数由小变大;
(3)无论在y轴右侧还是y轴左侧,底数按逆时针方向变大。三、指数函数图像的特点 例 如图是指数函数
① y=ax ② y=bx ③ y=cx ④ y=dx 的图象,
则 a,b,c,d 的大小关系为_______________b < a < 1 < d < c指数函数① f(x)=mx② g(x)=nx满足不等式1>n>m>0,则它们的图象是 (??? ) 指数函数一、定义: 函数 y = a x (a>0,且a≠1)
叫做指数函数,其中x是自变量.
二、性质:小结1.下列各函数中,是指数函数的是
A.y=(-3)x B.y=-3x C.y=3x-1 D.y=√当堂检测2.下面关于函数y=2x与y= 的性质的说法不正确的是
A.定义域都是R B.值域都为R
C.单调性不同 D.均过点(0,1)√3.若 则a,b,c的大小关系是
A.a>b>c B.aC.a2. 3.1.2 课后案
3.1.2 指数函数
学习目标1、了解指数函数模型的实际背景;
2、理解指数函数的概念、图像和性质。
指数函数的性质和应用。 重点难点指数函数的概念和性质。……情景1:一把长为1的尺子第一次截去它的一半,第二次截去剩余部分的一半,第三次截去第二次剩余部分的一半,依次截下去,问截的次数x与剩下的尺子长度y之间的关系.情景2:“ 木马病毒”被认为是破坏性极强的计算机病毒之一,具有快速自我复制能力,它可以由1个变成2个,2个变成4个……复制x次后,你知道所得病毒个数y与x的函数关系式是什么?复制
次数 x第1次第2次第3次第4次…...第x次 上述情景中的函数解析式有什么共同特征?2探究1指数幂形式
自变量在指数位置
底数是常量一、指数函数的定义 一般地,函数 y=a x(a>0 且 a ≠ 1,x ? R )叫做指数函数.其中 x 是自变量,定义域为 R.系数为1底数为大于0且
不为1的常数自变量为纯“x”,系数为1 概念剖析y =1,为常数函数没有研究的必要.思考:为何规定a?0,且a?1 ?a x有些会没有意义,如 a x有些会没有意义,如 y=a x当a<0时
当a=0时
当a=1时
例 指出下列函数哪些是指数函数:(1)y=(-3)x; (2) y=?x ;(3)y=0.7x; (4) y=x3.
(口答)判断下列函数是不是指 数函数,为什么?√√函数y=(a2-3a+3)ax是指数函数,求a的值.∴a=2011…0.0370.11
0.33
13927…
y=3-x…2793
10.330.110.037…
y=3x…321
0
-1
-2
-3
…
x(2) 与 的图象. 列表:关于y轴对称不是y=ax (0
R( 0 , + ∞)过定点 ( 0 , 1 ) 在R上是增函数在R上是减函数 定义域 值域 定点 单调性a > 10 < a < 1二、指数函数的图象和性质 指函图象半个八,
大一撇来小一捺,
图象必过(0,1)点,?
X轴上方为指家.? 例 用指数函数的性质,判断下列各
函数的单调性:解:(1)因为3>1, 例 比较下列各题中两个值的大小1.72.5与1.73
解:(1) 考虑指数函数 y=1.7x,它是增函数.∵2.5<3 ∴1.72.5<1.73.例 比较下列各题中两个值的大小 :1.72.5与1.73
解:(1) 考虑指数函数 y=1.7x它是增函数.∵2.5<3
∴1.72.5<1.73(2) 1.2与 5解:(2)考虑指数函数它是 .∵练习:比较100.2与1的大小.减函数1.2< 5∴底不同,指数也不同 利用函数图象或中间量进行比较底数相同,但需要分情况讨论 解:①②比较指数大小的方法①同底不同指:对于底数相同,指数不同的两个幂的大小比较,可以构造函数,利用函数的单调性,若底数是参变量要注意分类讨论。②不同底不同指:对于底数不同,指数不同的两个幂的大小比较用别的数如0或1做桥。③同指不同底:对于指数相同,底数不同的两个幂比较大小,可先构造函数,再利用指数函数图象变化规律来判断第一象限中,底大图高-1第二象限中,底大图低1、底数互为倒数的两个指数函数图像关于y轴对称2、 当a>1时, 底数越大,图像越陡
当 0
(1)y轴右侧,图像从下到上相应底数由小变大底大图高;
(2)Y轴左侧,图像从上到下相应底数由小变大;
(3)无论在y轴右侧还是y轴左侧,底数按逆时针方向变大。三、指数函数图像的特点 例 如图是指数函数
① y=ax ② y=bx ③ y=cx ④ y=dx 的图象,
则 a,b,c,d 的大小关系为_______________b < a < 1 < d < c指数函数① f(x)=mx② g(x)=nx满足不等式1>n>m>0,则它们的图象是 (??? ) 指数函数一、定义: 函数 y = a x (a>0,且a≠1)
叫做指数函数,其中x是自变量.
二、性质:小结1.下列各函数中,是指数函数的是
A.y=(-3)x B.y=-3x C.y=3x-1 D.y=√当堂检测2.下面关于函数y=2x与y= 的性质的说法不正确的是
A.定义域都是R B.值域都为R
C.单调性不同 D.均过点(0,1)√3.若 则a,b,c的大小关系是
A.a>b>c B.a
