4.2 换底公式 课件:17张PPT
文档属性
| 名称 | 4.2 换底公式 课件:17张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 244.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 18:05:48 | ||
图片预览






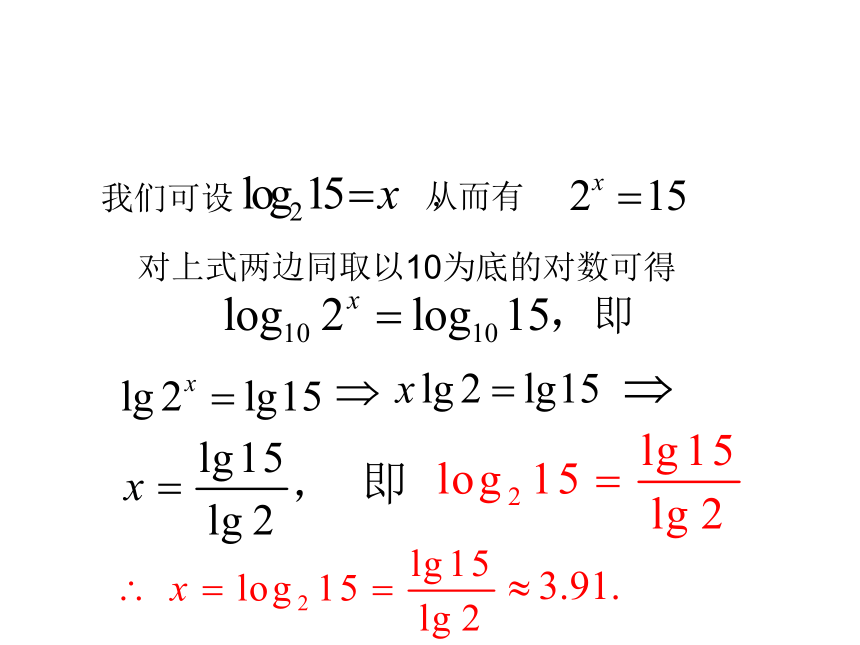
文档简介
课件17张PPT。 对 数 换 底 公 式
学习目标
1.掌握对数的换底公式,能推导和证明换底公式;(重点)
2.会用换底公式进行化简、求值。一、复习与回顾2、对数的运算性质1、对数的定义问题:对数的运算法则应用的前提是什么?
底数相同
如果底数不同怎么办?二、新知探究1、你能计算出它们各自的值吗?
2、它们的值有什么关系吗?问题:计算器通常只能对常用对数或自然对数进行计算,log25怎么计算?我们可设 ,对上式两边同取以10为底的对数可得从而有即由抽象推广到一般情况可得重要的对数转换公式:换底公式 说明:对数换底公式的证明方法并不唯一,前面对 的求值过程实际上就是一种证明方法,可类似证明对数换底公式,三、获取新知证明: 设x=logbN,根据对数定义,有
N=bx.
两边取以a为底的对数,得
logaN=logabx.
而logabx=xlogab,所以
logaN=xlogab.
由于b≠1,则logab≠0,解出x得因为x=logbN,所以对数换底公式换底公式好神奇
换成新底可任意
原底加底变分母
真数加底变分子如何证明四、知识应用六、公式推论推论1 推论2如何证明如何证明五、知识应用七、跟踪练习若lg2=a,lg3=b,请用a,b表示下列各式的值。思考:对数换底公式的作用是什么?思考:在进行对数的化简与计算时,如何选用底数?思考:在什么情况下选用对数换底公式?答:(1)在运算过程中,出现不能直接用计算器获得对数值时,可化为10为底的常用对数进行运算.
(2)在化简求值过程中,出现不同底数的对数不能运用运算法则时,可统一化成同一个底数为底的对数,再根据运算法则进行化简或求值.答:利用对数换底公式可以将不同底数的对数化为同底的对数;或将一般地对数化为自然对数或常用对数,这样便于计算.答:一般进行数值计算的可选用以10为底的常用对数,便于计算;若进行化简和证明,可选用被处理的式子中用的比较多的底数作为底数.对数换底公式两个推论你从这节课上学到了什么?八、课时小结转化思想:
1、“对数式”与“指数式”的互化
2、“不同底”化“同底”。九、课外作业
1.掌握对数的换底公式,能推导和证明换底公式;(重点)
2.会用换底公式进行化简、求值。一、复习与回顾2、对数的运算性质1、对数的定义问题:对数的运算法则应用的前提是什么?
底数相同
如果底数不同怎么办?二、新知探究1、你能计算出它们各自的值吗?
2、它们的值有什么关系吗?问题:计算器通常只能对常用对数或自然对数进行计算,log25怎么计算?我们可设 ,对上式两边同取以10为底的对数可得从而有即由抽象推广到一般情况可得重要的对数转换公式:换底公式 说明:对数换底公式的证明方法并不唯一,前面对 的求值过程实际上就是一种证明方法,可类似证明对数换底公式,三、获取新知证明: 设x=logbN,根据对数定义,有
N=bx.
两边取以a为底的对数,得
logaN=logabx.
而logabx=xlogab,所以
logaN=xlogab.
由于b≠1,则logab≠0,解出x得因为x=logbN,所以对数换底公式换底公式好神奇
换成新底可任意
原底加底变分母
真数加底变分子如何证明四、知识应用六、公式推论推论1 推论2如何证明如何证明五、知识应用七、跟踪练习若lg2=a,lg3=b,请用a,b表示下列各式的值。思考:对数换底公式的作用是什么?思考:在进行对数的化简与计算时,如何选用底数?思考:在什么情况下选用对数换底公式?答:(1)在运算过程中,出现不能直接用计算器获得对数值时,可化为10为底的常用对数进行运算.
(2)在化简求值过程中,出现不同底数的对数不能运用运算法则时,可统一化成同一个底数为底的对数,再根据运算法则进行化简或求值.答:利用对数换底公式可以将不同底数的对数化为同底的对数;或将一般地对数化为自然对数或常用对数,这样便于计算.答:一般进行数值计算的可选用以10为底的常用对数,便于计算;若进行化简和证明,可选用被处理的式子中用的比较多的底数作为底数.对数换底公式两个推论你从这节课上学到了什么?八、课时小结转化思想:
1、“对数式”与“指数式”的互化
2、“不同底”化“同底”。九、课外作业
