5.3 y=对数函数的图像和性质 课件:20张PPT
文档属性
| 名称 | 5.3 y=对数函数的图像和性质 课件:20张PPT | 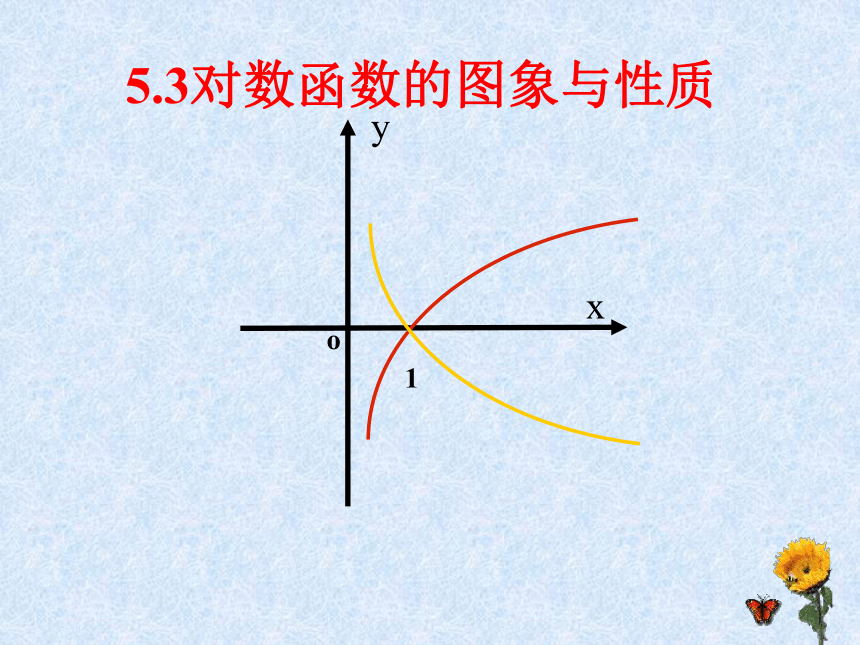 | |
| 格式 | zip | ||
| 文件大小 | 409.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 18:06:39 | ||
图片预览




文档简介
课件20张PPT。5.3对数函数的图象与性质1 学习目标 理解对数函数的概念。
2. 通过画对数函数的图象理解并掌握其性质。
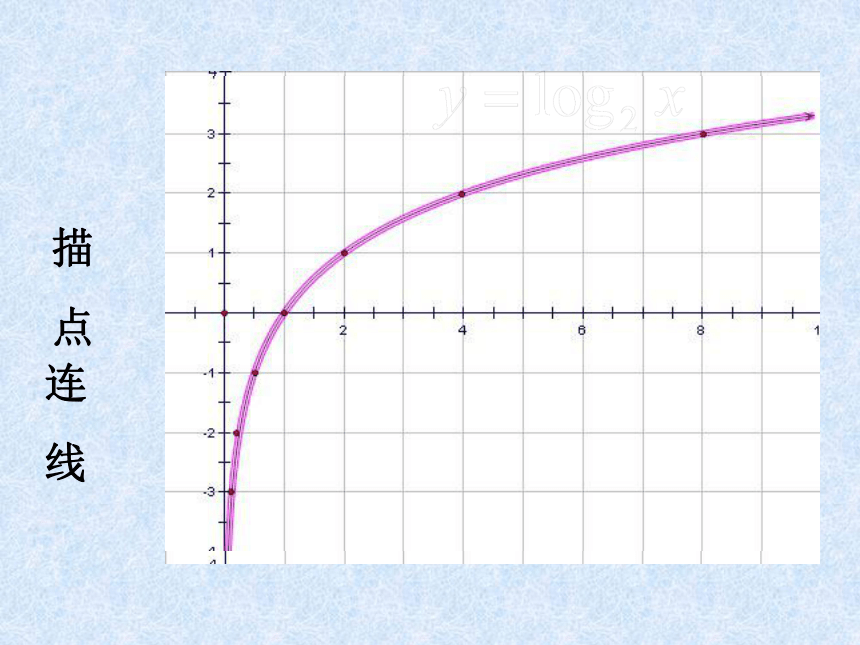
3. 能初步应用对数函数的性质解决简单问题。作图的基本步骤: (二)对数函数的图像和性质
1、取值列表(根据给定的自变量分
别计算出因变量的值)3. 连线(将所描的点用光滑的曲线
连接起来)2、描点(根据列表中的坐标分别在
坐标系中标出其对应点)
描点法
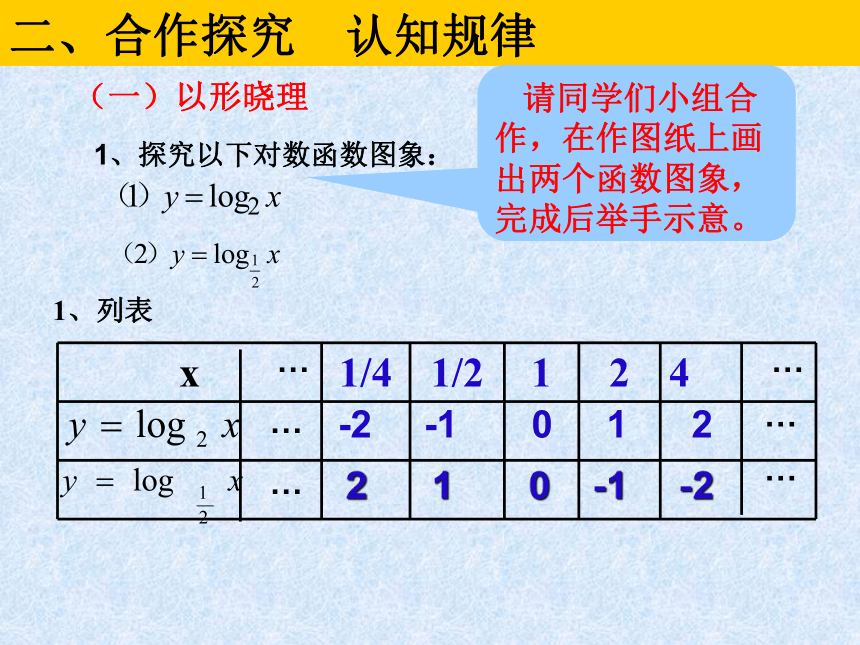
二、合作探究 认知规律 (一)以形晓理1、列表1、探究以下对数函数图象:… … … … … … -2 -1 0 1 2 2 1 0 -1 -2 请同学们小组合作,在作图纸上画出两个函数图象,完成后举手示意。
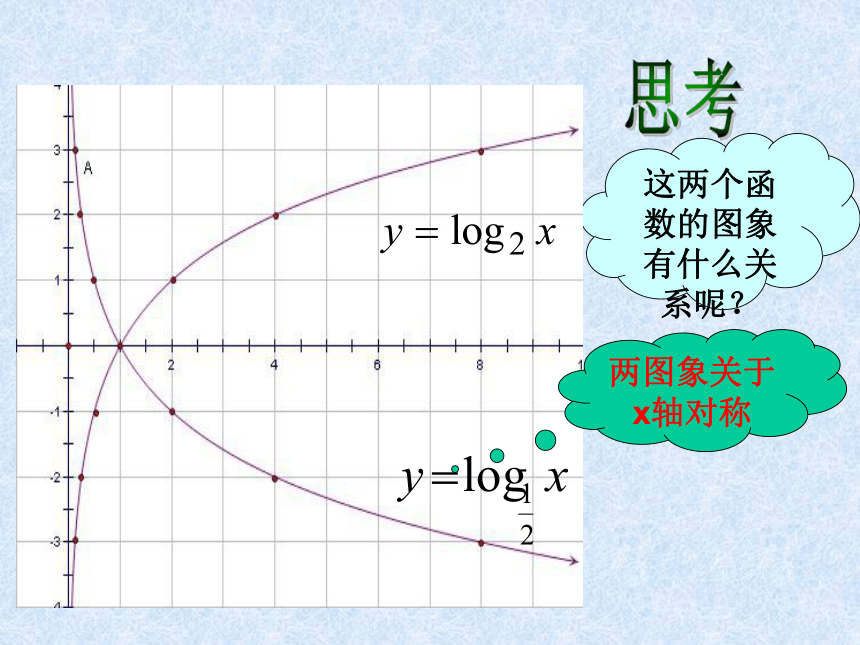
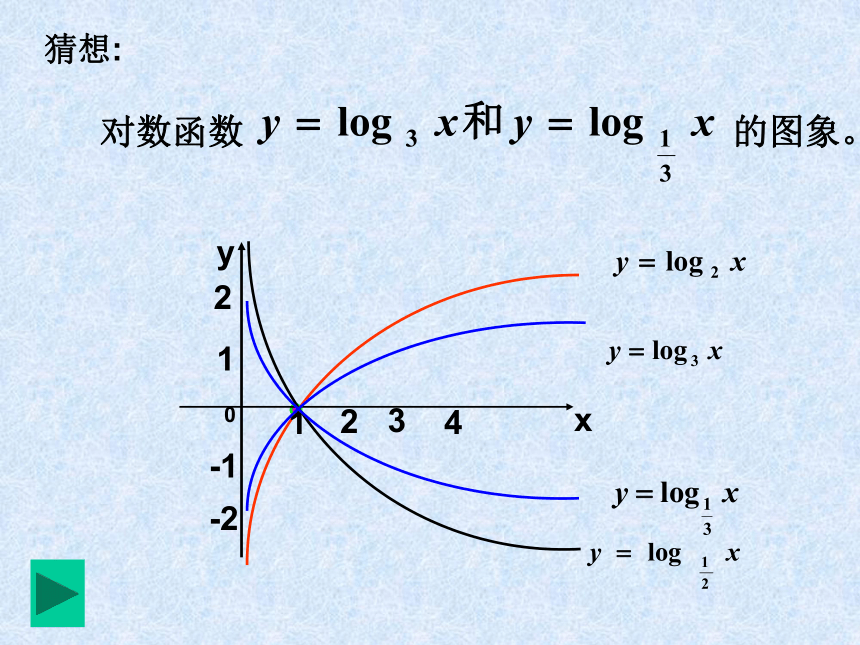
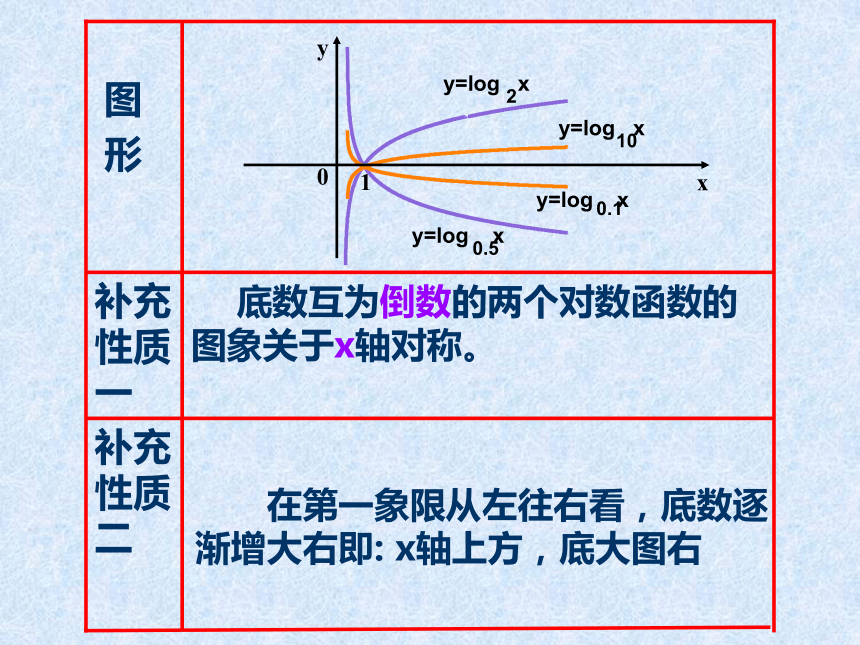
描 点连 线描 点连 线思考这两个函数的图象有什么关系呢?两图象关于x轴对称对数函数 的图象。猜想: 补充性质二 底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形1 在第一象限从左往右看,底数逐渐增大右即: x轴上方,底大图右y = log2 x与y = log 0.5 x的图像分析 (0,+∞)(0,+∞)RR增函数减函数(1,0)(1,0)0 x>1时,y>000
x>1时,y<0对数函数y = loga x的性质分析(0,+∞)R在(0,+∞)上是
增函数在(0,+∞)上是
减函数(1,0) 即loga1=0 底数a影响着对数函数的性质例题与练习例1,求下列函数的定义域: (3)练习:课本P96练习第2题合作探究例2:求函数图象过的定点
① y=1+logax ②y=loga(4-x) +3解: ① ∵ 当 x =1,即x=1时,y=1+loga1=2
∴函数y=1+logax的图象恒过定点(1,2)。 ② ∵当 4-x=1时,即x=3, y=loga(4-3)+3=3
∴函数y=loga(4-x)的图象恒过定点(3,3) 例3,比较下列各题中两个数的大小:(1) log25.3与 log24.7 (2) log 0.27与 log 0.2 9 解:(1)∵底数a=2 > 1, ∴函数y= log2x是增函数;
又∵ 5.3 > 4.7
∴ log25.3 > log24.7 (2)∵底数a=0.2 <1, ∴函数y= log0.2x是减函数;
又∵ 7 < 9
∴ log0.27 > log0.29 底数a影响着对数函数的性质 比较下列各组中两个值的大小:
⑴ log 67 , log 7 6 ; ⑵ log 3π , log 2 0.8 . 解: ⑴∵log67>log66=1
又∵ log76<log77=1
∴ log67>log76 ⑵ ∵log3π>log31=0
又 ∵ log20.8<log21=0
∴ log3π>log20.8提示 : log aa=1提示: log a1=0自主检测对数函数概念对数函数图象对数函数性质对数函数自主小结自主小结1.对数函数的定义2.求定义域3.求函数图象过的的定点本节题型 4.用对数函数性质比较大小作业:
1.(课后思考):对数函数与指数函数图像的关系提示:分别将和和的图像画在一个坐标系内,观察图像的特点!2.教材第97页习题3——5A组第4,5,6题。再见
2. 通过画对数函数的图象理解并掌握其性质。
3. 能初步应用对数函数的性质解决简单问题。作图的基本步骤: (二)对数函数的图像和性质
1、取值列表(根据给定的自变量分
别计算出因变量的值)3. 连线(将所描的点用光滑的曲线
连接起来)2、描点(根据列表中的坐标分别在
坐标系中标出其对应点)
描点法
二、合作探究 认知规律 (一)以形晓理1、列表1、探究以下对数函数图象:… … … … … … -2 -1 0 1 2 2 1 0 -1 -2 请同学们小组合作,在作图纸上画出两个函数图象,完成后举手示意。
描 点连 线描 点连 线思考这两个函数的图象有什么关系呢?两图象关于x轴对称对数函数 的图象。猜想: 补充性质二 底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形1 在第一象限从左往右看,底数逐渐增大右即: x轴上方,底大图右y = log2 x与y = log 0.5 x的图像分析 (0,+∞)(0,+∞)RR增函数减函数(1,0)(1,0)0
x>1时,y<0对数函数y = loga x的性质分析(0,+∞)R在(0,+∞)上是
增函数在(0,+∞)上是
减函数(1,0) 即loga1=0 底数a影响着对数函数的性质例题与练习例1,求下列函数的定义域: (3)练习:课本P96练习第2题合作探究例2:求函数图象过的定点
① y=1+logax ②y=loga(4-x) +3解: ① ∵ 当 x =1,即x=1时,y=1+loga1=2
∴函数y=1+logax的图象恒过定点(1,2)。 ② ∵当 4-x=1时,即x=3, y=loga(4-3)+3=3
∴函数y=loga(4-x)的图象恒过定点(3,3) 例3,比较下列各题中两个数的大小:(1) log25.3与 log24.7 (2) log 0.27与 log 0.2 9 解:(1)∵底数a=2 > 1, ∴函数y= log2x是增函数;
又∵ 5.3 > 4.7
∴ log25.3 > log24.7 (2)∵底数a=0.2 <1, ∴函数y= log0.2x是减函数;
又∵ 7 < 9
∴ log0.27 > log0.29 底数a影响着对数函数的性质 比较下列各组中两个值的大小:
⑴ log 67 , log 7 6 ; ⑵ log 3π , log 2 0.8 . 解: ⑴∵log67>log66=1
又∵ log76<log77=1
∴ log67>log76 ⑵ ∵log3π>log31=0
又 ∵ log20.8<log21=0
∴ log3π>log20.8提示 : log aa=1提示: log a1=0自主检测对数函数概念对数函数图象对数函数性质对数函数自主小结自主小结1.对数函数的定义2.求定义域3.求函数图象过的的定点本节题型 4.用对数函数性质比较大小作业:
1.(课后思考):对数函数与指数函数图像的关系提示:分别将和和的图像画在一个坐标系内,观察图像的特点!2.教材第97页习题3——5A组第4,5,6题。再见
