2019秋八年级数学上册14.2勾股定理的应用课件(16张ppt)华东师大版
文档属性
| 名称 | 2019秋八年级数学上册14.2勾股定理的应用课件(16张ppt)华东师大版 |

|
|
| 格式 | zip | ||
| 文件大小 | 611.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-10 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
14.2 勾股定理的应用
第14章 勾股定理
导入新课
讲授新课
当堂练习
课堂小结
情境引入
学习目标
1.能运用勾股定理及其逆定理解决简单的实际问题.(重点)
2.经历勾股定理的应用过程,熟练掌握其应用方法,明确应用条件.(难点)
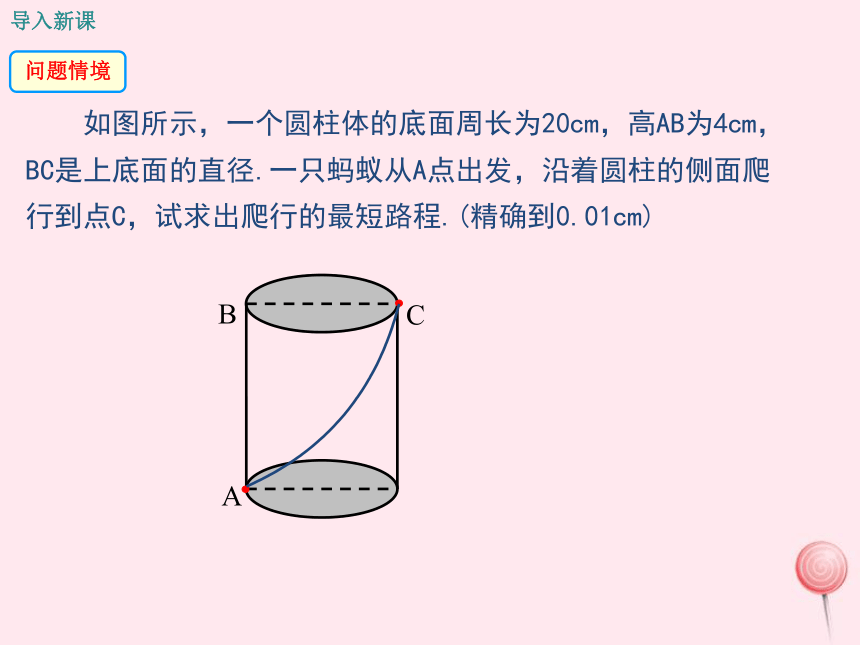
如图所示,一个圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从A点出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.(精确到0.01cm)
导入新课
问题情境
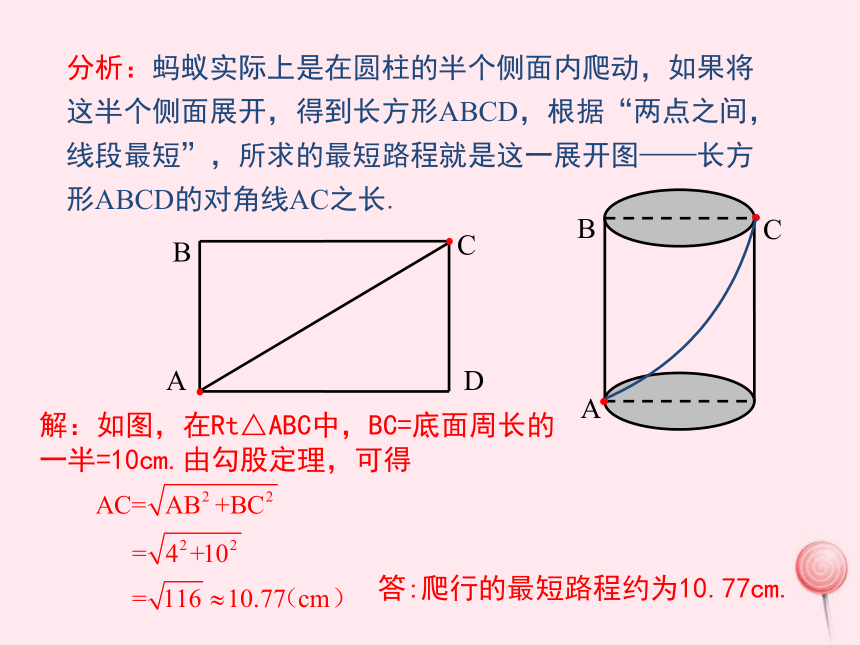
分析:蚂蚁实际上是在圆柱的半个侧面内爬动,如果将这半个侧面展开,得到长方形ABCD,根据“两点之间,线段最短”,所求的最短路程就是这一展开图——长方形ABCD的对角线AC之长.
把几何体适当展开成平面图形,再利用“两点之间,线段最短”性质来解决问题.
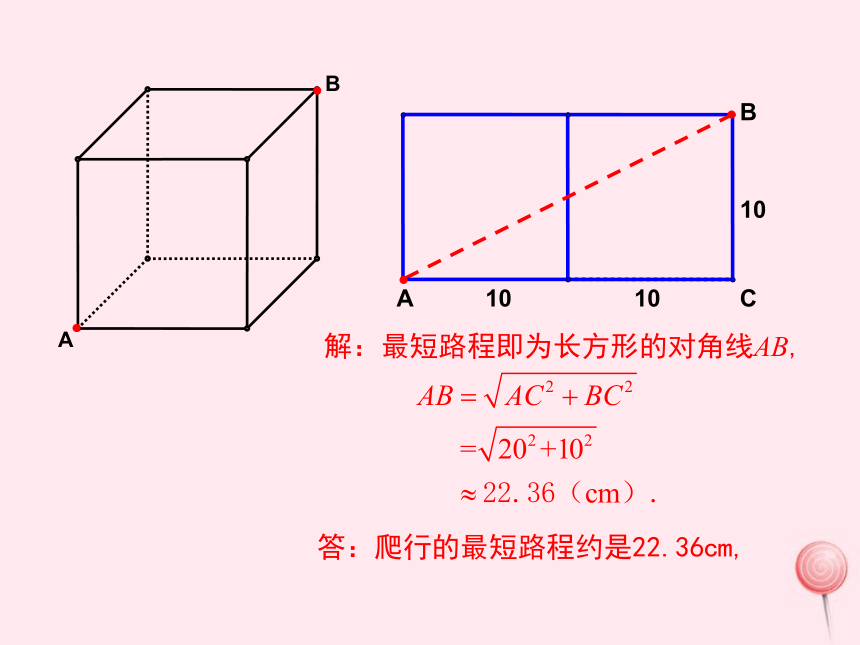
例1 如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?(精确到0.01cm)
讲授新课
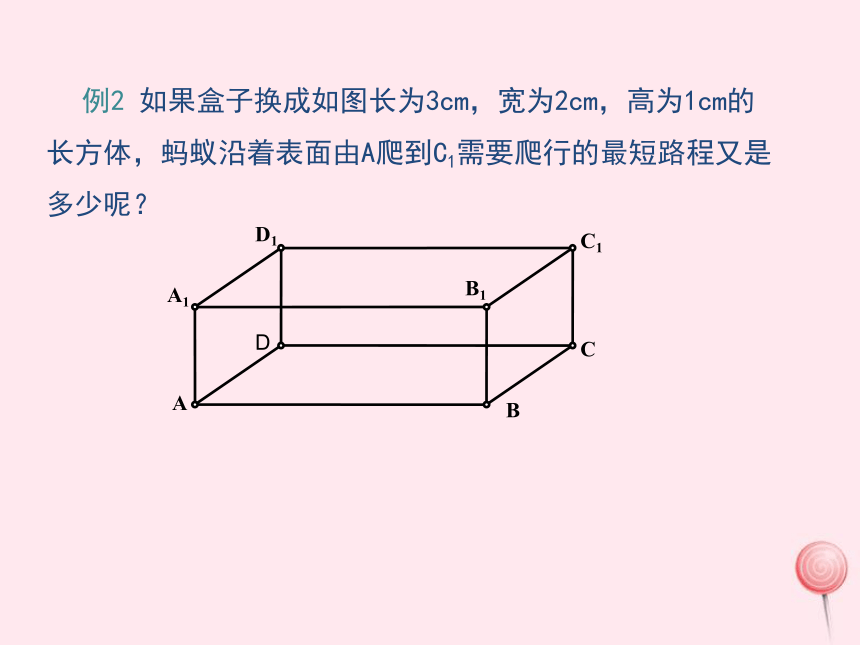
例2 如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面由A爬到C1需要爬行的最短路程又是多少呢?
分析:蚂蚁由A爬到C1过程中较短的路线有多少种情况?
(1)经过前面和上底面;
(2)经过前面和右面;
(3)经过左面和上底面.
B
C
D
B1
C1
D1
A1
(1)当蚂蚁经过前面和上底面时,如图,最短路程为
解:
AB=
≈4.24(cm).
=
B
C
D
B1
C1
D1
A1
(2)当蚂蚁经过前面和右面时,如图,最短路程为
AB=
≈5.10(cm).
=
B
C
D
B1
C1
D1
A1
(3)当蚂蚁经过左面和上底面时,如图,最短路程为
AC1=
≈4.47(cm).
=
B
C
D
B1
C1
D1
A1
∴最短路程约为4.24cm.
∵4.24<4.47<5.10,
例3 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由.
2米
2.3米
CD=
CH=0.6+2.3=2.9(米)>2.5(米).
答:卡车能通过厂门.
解:在Rt△OCD中,∠CDO=90°,由勾股定理,得
2米
2.3米
1.如图,已知CD=6cm,AD=8cm, ∠ADC=90o,BC=24cm,AB=26cm,求阴影部分面积.
当堂练习
解:在Rt△ADC中,
∵AC2=AD2+CD2(勾股定理)
=82+62=100,
∴AC=10.
∵AC2+BC2=102+242=676=262,
∴△ACB为直角三角形(勾股定理的逆定理).
∴S阴影部分=S△ACB-S△ACD
=120-24
=96.
2.如图,在△ABC中,AB=AC,D点在CB 延长线上,求证:AD2-AB2=BD·CD
E
勾股定理的应用
最短路程问题
课堂小结
勾股定理与其逆定理的应用
14.2 勾股定理的应用
第14章 勾股定理
导入新课
讲授新课
当堂练习
课堂小结
情境引入
学习目标
1.能运用勾股定理及其逆定理解决简单的实际问题.(重点)
2.经历勾股定理的应用过程,熟练掌握其应用方法,明确应用条件.(难点)
如图所示,一个圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从A点出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.(精确到0.01cm)
导入新课
问题情境
分析:蚂蚁实际上是在圆柱的半个侧面内爬动,如果将这半个侧面展开,得到长方形ABCD,根据“两点之间,线段最短”,所求的最短路程就是这一展开图——长方形ABCD的对角线AC之长.
把几何体适当展开成平面图形,再利用“两点之间,线段最短”性质来解决问题.
例1 如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?(精确到0.01cm)
讲授新课
例2 如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面由A爬到C1需要爬行的最短路程又是多少呢?
分析:蚂蚁由A爬到C1过程中较短的路线有多少种情况?
(1)经过前面和上底面;
(2)经过前面和右面;
(3)经过左面和上底面.
B
C
D
B1
C1
D1
A1
(1)当蚂蚁经过前面和上底面时,如图,最短路程为
解:
AB=
≈4.24(cm).
=
B
C
D
B1
C1
D1
A1
(2)当蚂蚁经过前面和右面时,如图,最短路程为
AB=
≈5.10(cm).
=
B
C
D
B1
C1
D1
A1
(3)当蚂蚁经过左面和上底面时,如图,最短路程为
AC1=
≈4.47(cm).
=
B
C
D
B1
C1
D1
A1
∴最短路程约为4.24cm.
∵4.24<4.47<5.10,
例3 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由.
2米
2.3米
CD=
CH=0.6+2.3=2.9(米)>2.5(米).
答:卡车能通过厂门.
解:在Rt△OCD中,∠CDO=90°,由勾股定理,得
2米
2.3米
1.如图,已知CD=6cm,AD=8cm, ∠ADC=90o,BC=24cm,AB=26cm,求阴影部分面积.
当堂练习
解:在Rt△ADC中,
∵AC2=AD2+CD2(勾股定理)
=82+62=100,
∴AC=10.
∵AC2+BC2=102+242=676=262,
∴△ACB为直角三角形(勾股定理的逆定理).
∴S阴影部分=S△ACB-S△ACD
=120-24
=96.
2.如图,在△ABC中,AB=AC,D点在CB 延长线上,求证:AD2-AB2=BD·CD
E
勾股定理的应用
最短路程问题
课堂小结
勾股定理与其逆定理的应用
