苏教版小学五年级数学上册 第7章 解决问题的策略 单元测试题(有答案)
文档属性
| 名称 | 苏教版小学五年级数学上册 第7章 解决问题的策略 单元测试题(有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 363.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 00:00:00 | ||
图片预览




文档简介
苏教版小学五年级数学上册 第7章 解决问题的策略 单元测试题
一.选择题(共10小题,满分20分,每小题2分)
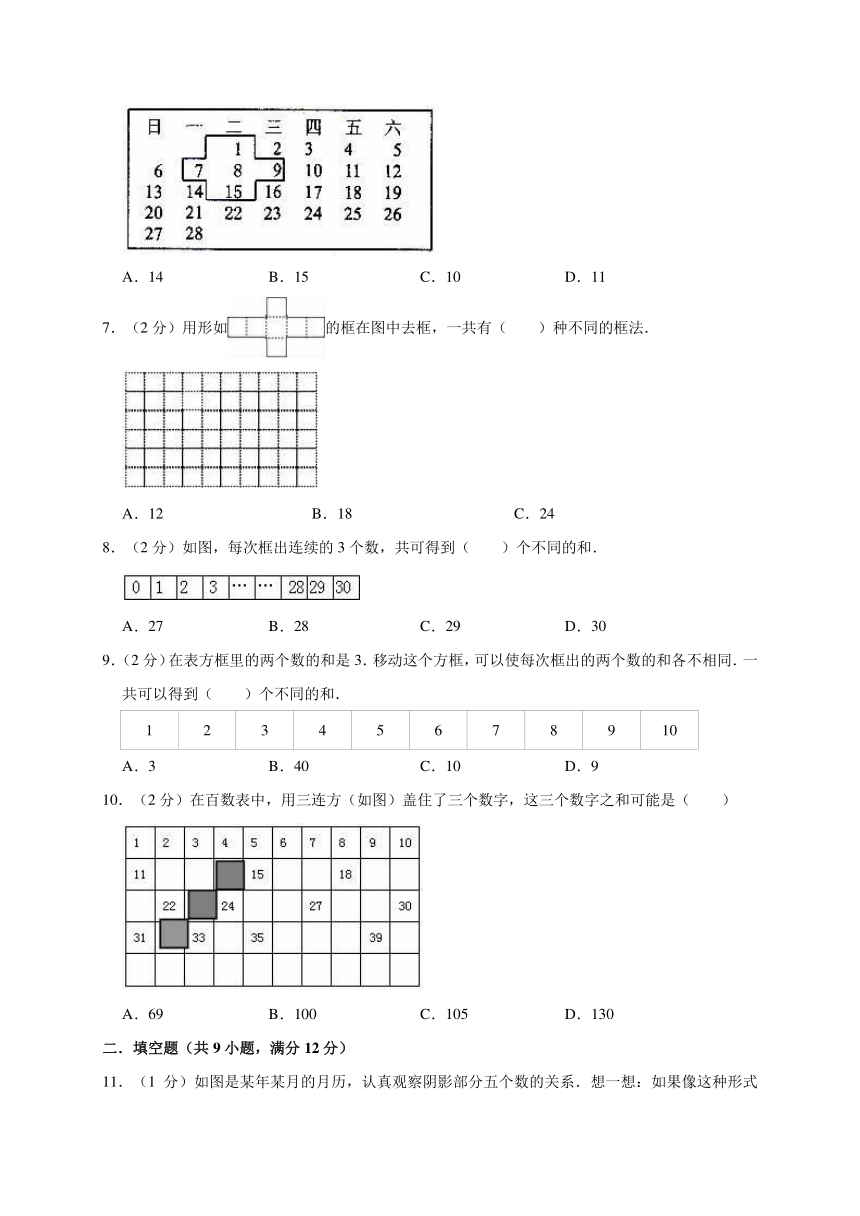
1.(2分)小强观察一个建筑物模型(由若干个相同的小正方体拼成),分别从前面,右面,上面观察,看到的图案如图所示,那么该模型共由( )个小正方体拼成.
A.8 B.9 C.10 D.11
2.(2分)10张连号的世博园如愿券,张老师一家人要拿3张连号的,共有( )种不同的拿法.
A.6 B.7 C.8
3.(2分)如图,五个正方形重叠,连结点正好是正方形的中点,正方形的边长都是a,如图的周长是 ( )
A.24a B.18a C.14a D.12a.
4.(2分)在下面的数表中,每次框出2个数,一共有( )种不同的和.
2 3 4 5 6 7 8 9 10 11 12 13
A.12 B.11 C.10 D.9
5.(2分)有15个连续的自然数,每次用长方形框出4个连续的自然数,一共有( )种不同的框法.
A.10 B.11 C.12
6.(2分)在下面的月历卡中,用“十”字形框5个数,共可以框出( )个不同的和.
A.14 B.15 C.10 D.11
7.(2分)用形如的框在图中去框,一共有( )种不同的框法.
A.12 B.18 C.24
8.(2分)如图,每次框出连续的3个数,共可得到( )个不同的和.
A.27 B.28 C.29 D.30
9.(2分)在表方框里的两个数的和是3.移动这个方框,可以使每次框出的两个数的和各不相同.一共可以得到( )个不同的和.
1 2 3 4 5 6 7 8 9 10
A.3 B.40 C.10 D.9
10.(2分)在百数表中,用三连方(如图)盖住了三个数字,这三个数字之和可能是( )
A.69 B.100 C.105 D.130
二.填空题(共9小题,满分12分)
11.(1分)如图是某年某月的月历,认真观察阴影部分五个数的关系.想一想:如果像这种形式的五个数的和为105,则中间的那个数是 .
12.(1分)在如图中,每次框出连续4个自然数,共可得到 个不同的和.
13.(2分)如图是2013年8月的月历卡,用形如的长方形去框月历卡里的日期数,每次同时框出3个数.框出的3个数和最大的是 ,一共可以框出 种不同的和.
14.(1分)在1、2、3、4、5、6、7、8中,每次选出4个连续的数求和,一共可以有 种不同的和.
15.(1分)如图是一条带花的彩带.如果剪3朵花连在一起的彩带,一共有 不同的剪法.
16.(2分)如图是小林卧室一面墙上贴的瓷砖,中间 块组成了一个图案.在保持组合图案不变的情况下,有 种不同贴法.
17.(1分)今年“国庆七日长假”,明明想参加“西湖两日游”,哪两日去呢,他共有 不同的选择.
18.(2分)在下表中每次框出2个相邻的数,一共可以得到 个不同的和;如果每次框出3个相邻的数,一共可以得到 个不同的和.
1 2 3 4 5 6 7 8 9 10
19.(1分)下面一排圆圈共有15个,如果要给相邻的4个涂上红色.一共有 种不同的涂法.
三.操作题(共6小题,满分30分,每小题5分)
20.(5分)如图是2010年5月的台历.
(1)小明的爸爸每上4天班休息一天,妈妈却是上3天班休息一天,5月2日爸爸、妈妈都在家休息,下一次他们同时在家休息是星期 .
(2)算一算,上表中被阴影覆盖的5个数的和与中间的数有什么关系?(计算后再说明)
(3)如果框出的5个数的和是75,那么这5个数分别是多少,在图中框出来.
(4)一共可以框出 个不同的和.
21.(5分)如图是2008年1月的月历表,表中用“十”字框每次框出5个数(不能少框).
(1)用“十”字框任意框几次,框中5个数的和是正中间一个数的 倍.
(2)如果“十”字框正中间一个数为x,5个数的和为90,那么x的值是 .
22.(5分)下面的每一个图形都是由中的两个构成的.观察各个图形,根据图下表示的数,找出规律,画出表示31的图形.
23.(5分)根据前三幅图的变化规律画出第四幅图.
24.(5分)算一算,框一框.
(1)用长方形在上面的月历卡上框出三个数,使这三个数的和等于48.
(2)用正方形框出9个数,使这九个数的和等于99.
25.(5分)(1)图是2008年10的月历卡,用形如的长方形去框月历卡里的日期数,每次同时框出3个数,框出的3个数的和最大是 ,最小是 ,一共可以框出 种不同的和.
(2)请你用框出和是87的3个数.
四.解答题(共7小题,满分38分)
26.(5分)将1﹣1001的自然数按如表方式排列,用一个方框框出九个数,要使这九个数的和等于2007或2008,你能否办到?如果你能请分别写出这个方框中的最大数和最小数.
A 当这九个数的和是2007时,能否办到,如果能方框中最大数是 ,最小数是 ;
B当这九个数的和是2008时,能否办到,如果能方框中最大数是?最小数是?
27.(5分)日历的规律:认真观察如图阴影方框中正中间的数与其他4个数的关系.
(1)中间数是x,则左边的数是x﹣1,右边的数是x+1,上面的数是 ,下面的数是 .
(2)方框中5个数之和与该方框中间的数有什幺关系?
(3)当5个数的和是80时,中间的数是多少?
28.(5分)仔细观察如图,任意框出四个数,请将表格中其余三个数用含有字母的式子表示出来.
如果框出的四个数的和是84,那么这四个数分别是多少?
29.(6分)表中一共有50个奇数,黑线框出的5个数之和是115;仔细观察后回答问题.
(1)你能发现每次框出的5个数的和与中间数有什么关系吗?
(2)如果框出5个数的和要是375,应该怎么框?(先在图中框一框,并在下面用文字说明)
(3)能框出和是295的5个数吗?为什么?
(4)一共可以框出多少个大小不同的和?
30.(5分)下表中粗线框中三个数的和是9.在表中移动这个粗线框,可以使每次框出的三个数的和各不相同.
(1)一共可以框出多少个不同的和?
(2)能框出和是64的三个数吗?为什么?
31.(6分)探索与实践:认真观察月历表的规律,如图阴影方框中正中间的数与其他四个数的关系.
(1)正中间的数是y,左边的数是 ,右边的数是 ,上面的数是 ,下面的数是 .
(2)方框中5个数之和与该方框正中间的数有什么关系?
(3)当5个数的和是115时,正中间的数是 .
32.(6分)如图是一张4×4的方格图,它由16个小正方形组成,每个小正方形里都写了一个数.
(1)在这个方格图上框出形,那么框出的4个数的和一共有多少种?其中和最大是多少?最小呢?
(2)在这个方格图上框出形,那么框出的5个数的和一共有多少种?每5个数的和一定是15的倍数吗?为什么?
参考答案与试题解析
一.选择题(共10小题,满分20分,每小题2分)
1.解:通过观察与想象知道该模型共由9个小正方体拼成.
即3+2+1+1+2=9(个).
故选:B.
2.解:给这10张如愿券编号为1~10,
只有第9、10号不能放在开头,所以一共有:
10﹣2=8(种);
答:共有8种不同的拿法.
故选:C.
3.解:3a+3a+2a×3=12a,
答:这个图形的周长是12a.
故选:D.
4.解:数字数:13﹣2+1=12(个)
不同的和数:12﹣2+1=11(个)
答:一共有11种不同的和.
故选:B.
5.解:相邻的4个数有15﹣4+1=12种情况,
则有12种不同的和,即一共有12种不同的框法.
故选:C.
6.解:观察图形可知:中间数只能在第二、三、四行,而且中间数的上下左右必须有数,那么:
第二行的中间数可以是:8,9,10,11;
第三行的中间数可以是:14,15,16,17,18;
第四行的中间数可以是:21;
一共有4+5+1=10(个);
有10个不同的中间数,就有10个不同的和.
故选:C.
7.解:由分析得出:不同的框法有:6×4=24(种).
答:一共有24种不同的框法.
故选:C.
8.解:31﹣2=29(个).
答:共可得到29个不同的和.
故选:C.
9.解:10﹣1=9(中);
答:一共可以得到9个不同的和.
故选:D.
10.解:根据题干分析可得:14+23+32=69
答:这三个数字之和可能是69.
故选:A.
二.填空题(共9小题,满分12分)
11.解:因为像这种形式五个数的和是105,
那么五个数的和是中间的数的5倍,
所以中间的数是:105÷5=21,
即中间的那个数是21.
故答案为:21.
12.解:40﹣2+1﹣3
=39﹣3
=36
故共可得到36个不同的和.
故答案为:36.
13.解:29+30+31
=59+31
=90
1+5×4=21(种)
答:框出的3个数和最大的是 90,一共可以框出 21种不同的和.
故答案为:90,21.
14.解:依次选出4个连续的数可以为:1、2、3、4; 2、3、4、5; 3、4、5、6; 4、5、6、7; 5、6、7、8.
所以每次选出4个连续的数求和,一共可以有5种不同的和.
故答案为:5.
15.解:8﹣2=6(种)
答:一共有6种不同的剪法.
故答案为:6种.
16.解:贴法如下图:
(11﹣3+1)×(6﹣2+1)
=9×5
=45(种)
答:在保持组合图案不变的情况下,有45种不同的贴法.
故答案为:6,45.
17.解:明明可以选择以下的两天去旅游:
10月1日和10月2日;10月2日和10月3日;10月3日和0月4日;10月4日和10月5日;10月5日和10月6日;10月6日和10月7日;共6种选择.
故答案为:6种.
18.解:根据题干分析可得:
(1)如果每次框出2个数,可以得到9个不同的和.
(2)如果每次框出3个数,可以得到8个不同的和.
故答案为:9,8.
19.解:15﹣4+1=12(种);
答:一共有12种不同的涂法.
故答案为:12.
三.操作题(共6小题,满分30分,每小题5分)
20.解:(1)5和4是互质数,所以5和4的最小公倍数是:5×4=20,
所以5月2日,他们同时休息,那么下一次他们同时休息是:2+20=22,即5月22日,星期六;
(2)上表中被阴影覆盖的5个数和是:11+17+18+19+25=90;
90÷18=5,所以这5个数的和是中间的数的5倍;
(3)因为这5个数的和是中间的数的5倍,所以中间数是75÷5=15,则框出的5个数为:8、14、15、16、22;
如图:
(4)1+5×2=11(个)
所以,一共可以框出11个不同的和.
故答案为:六、11.
21.解:(1)1+7+8+9+15=40=8×5
2+8+9+10+16=45=9×5
3+9+10+11+17=50=10×5
所以可得:框出的5个数的和是中间数的5倍.
(2)90÷5=18
答:x的值是18;
故答案为:5,18.
22.解:31由圆和平行四边形组成,且圆大,平行四边形小,如图:
23.解:根据图形的旋转规律,如图:
24.解:(1)48÷3=16,这三个数分别是15、16、17(用红色长方形框出).
(2)99÷3÷3=11,即这九个数中间的一个数是11,这九个分别是:3、4、5、10、11、12、17、18、19(用绿色正方形框出).
25.解:(1)29+30+31=90
1+2+3=6
2+5+5+5+4=21(种)
答:框出的3个数和最大的是90,最小是6,一共可以框出21种不同的和.
(2)87÷3=29,中间的数是29,前一个数是28,后一个数是30,所以:
故答案为:90,6,21.
四.解答题(共7小题,满分38分)
26.解:设方框内最小的数(左上角)为a,则框内的九个数可分别表示为:a,a+1,a+2,a+7,a+7+1,a+7+2,a+7×2,a+7×2+1,a+7×2+2.
它们的和是9a+7×3+7×2×3+(1+2)×3=9×(a+8).
由于总和9×(a+8)是9的倍数,
所以总和是2008不可能,只可能是2007.
当方框内9个数的和是2007时,框内的最小数是2007÷9﹣8=215,最大数是215+7×2+2=231;
答:方框中的最大数是231,最小数是215.
故答案为:231,215.
27.解:(1)由分析得出:中间数是x,则左边的数是x﹣1,右边的数是x+1,上面的数是x﹣7,下面的数是x+7;
(2)左边五个数的和是:7+13+14+15+21=70,70是中间的数14的5倍;右边五个数的和是:4+10+11+12+18=55,55是中间的数11的5倍;
所以得出:方框中5个数之和是该方框中间的数的5倍;
(3)中间的数都是:80÷5=16.
答:中间的数是16.
故答案为:(1)x﹣7;x+7;(2)方框中5个数之和是该方框中间的数的5倍;(3)中间的数是16.
28.解:
因为17+18+24+25=84,所以这四个数分别是17、18、24、25.
29.解:(1)通过每次框出的5个数,发现:115÷23=5倍,所以5个数之和正好是中间数的5倍;
(2)375÷5=75,框出的5个数的中间的数是75,所以框法为:
(3)295÷5=59
因为59在所给表的最右边,不能被框为中间的数,
所以,不能框出和是295的5个数;
(4)根据所给框的例子,知道23、25、27、29、31、33、35、37、及它们对应的下两行的数,都可以被框为中间的数,
所以,一共可以框出大小不同的和的个数:8×3=24(个).
答:一共可以框出24个大小不同的和.
30.解:(1)1﹣29共有15个数字,每次框出3个数字,一共有15﹣2=13(种)框法,所以有13个不同的和.
答:一共可以框出13个不同的和.
(2)由题意可知框出的三个数的和是3的倍数,因为64不是3的倍数,所以不能框出和是64的三个数.
答:不能框出和是64的三个数.因为框出的三个数的和是3的倍数,因为64不是3的倍,所以不能框出和是64的三个是.
31.解:(1)由分析得出:
中间数是x,则左边的数是x﹣1,右边的数是x+1,上面的数是x﹣7,下面的数是x+7;
(2)左边五个数的和是:7+13+14+15+21=70,70是中间的数14的5倍;右边五个数的和是:4+10+11+12+18=55,55是中间的数11的5倍;
所以得出:方框中5个数之和是该方框中间的数的5倍
答:方框中5个数之和是该方框中间的数的5倍.
(3)中间的数都是:115÷5=23.
答:当5个数的和是115时,正中间的数是23.
故答案为:(1)y﹣1,y+1,y﹣7;y+7.
32.解:(1)竖着有3种框法,横着有2种框法,
一共有3×2=6种,即出的4个数的和一共有6种;
最大是30+42+45+48=165
最小是3+15+18+21=57
(2)横着有2种框法,竖着也有2种框法,一共有2×2=4种框法,框出的5个数的和一共有4种;
根据框中心数与周围数的关系,可得和是中心数的5倍,中心的数18、21、30、33都是3的整数倍,5×3=15,所以每5个数的和一定是15的倍数.
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)小强观察一个建筑物模型(由若干个相同的小正方体拼成),分别从前面,右面,上面观察,看到的图案如图所示,那么该模型共由( )个小正方体拼成.
A.8 B.9 C.10 D.11
2.(2分)10张连号的世博园如愿券,张老师一家人要拿3张连号的,共有( )种不同的拿法.
A.6 B.7 C.8
3.(2分)如图,五个正方形重叠,连结点正好是正方形的中点,正方形的边长都是a,如图的周长是 ( )
A.24a B.18a C.14a D.12a.
4.(2分)在下面的数表中,每次框出2个数,一共有( )种不同的和.
2 3 4 5 6 7 8 9 10 11 12 13
A.12 B.11 C.10 D.9
5.(2分)有15个连续的自然数,每次用长方形框出4个连续的自然数,一共有( )种不同的框法.
A.10 B.11 C.12
6.(2分)在下面的月历卡中,用“十”字形框5个数,共可以框出( )个不同的和.
A.14 B.15 C.10 D.11
7.(2分)用形如的框在图中去框,一共有( )种不同的框法.
A.12 B.18 C.24
8.(2分)如图,每次框出连续的3个数,共可得到( )个不同的和.
A.27 B.28 C.29 D.30
9.(2分)在表方框里的两个数的和是3.移动这个方框,可以使每次框出的两个数的和各不相同.一共可以得到( )个不同的和.
1 2 3 4 5 6 7 8 9 10
A.3 B.40 C.10 D.9
10.(2分)在百数表中,用三连方(如图)盖住了三个数字,这三个数字之和可能是( )
A.69 B.100 C.105 D.130
二.填空题(共9小题,满分12分)
11.(1分)如图是某年某月的月历,认真观察阴影部分五个数的关系.想一想:如果像这种形式的五个数的和为105,则中间的那个数是 .
12.(1分)在如图中,每次框出连续4个自然数,共可得到 个不同的和.
13.(2分)如图是2013年8月的月历卡,用形如的长方形去框月历卡里的日期数,每次同时框出3个数.框出的3个数和最大的是 ,一共可以框出 种不同的和.
14.(1分)在1、2、3、4、5、6、7、8中,每次选出4个连续的数求和,一共可以有 种不同的和.
15.(1分)如图是一条带花的彩带.如果剪3朵花连在一起的彩带,一共有 不同的剪法.
16.(2分)如图是小林卧室一面墙上贴的瓷砖,中间 块组成了一个图案.在保持组合图案不变的情况下,有 种不同贴法.
17.(1分)今年“国庆七日长假”,明明想参加“西湖两日游”,哪两日去呢,他共有 不同的选择.
18.(2分)在下表中每次框出2个相邻的数,一共可以得到 个不同的和;如果每次框出3个相邻的数,一共可以得到 个不同的和.
1 2 3 4 5 6 7 8 9 10
19.(1分)下面一排圆圈共有15个,如果要给相邻的4个涂上红色.一共有 种不同的涂法.
三.操作题(共6小题,满分30分,每小题5分)
20.(5分)如图是2010年5月的台历.
(1)小明的爸爸每上4天班休息一天,妈妈却是上3天班休息一天,5月2日爸爸、妈妈都在家休息,下一次他们同时在家休息是星期 .
(2)算一算,上表中被阴影覆盖的5个数的和与中间的数有什么关系?(计算后再说明)
(3)如果框出的5个数的和是75,那么这5个数分别是多少,在图中框出来.
(4)一共可以框出 个不同的和.
21.(5分)如图是2008年1月的月历表,表中用“十”字框每次框出5个数(不能少框).
(1)用“十”字框任意框几次,框中5个数的和是正中间一个数的 倍.
(2)如果“十”字框正中间一个数为x,5个数的和为90,那么x的值是 .
22.(5分)下面的每一个图形都是由中的两个构成的.观察各个图形,根据图下表示的数,找出规律,画出表示31的图形.
23.(5分)根据前三幅图的变化规律画出第四幅图.
24.(5分)算一算,框一框.
(1)用长方形在上面的月历卡上框出三个数,使这三个数的和等于48.
(2)用正方形框出9个数,使这九个数的和等于99.
25.(5分)(1)图是2008年10的月历卡,用形如的长方形去框月历卡里的日期数,每次同时框出3个数,框出的3个数的和最大是 ,最小是 ,一共可以框出 种不同的和.
(2)请你用框出和是87的3个数.
四.解答题(共7小题,满分38分)
26.(5分)将1﹣1001的自然数按如表方式排列,用一个方框框出九个数,要使这九个数的和等于2007或2008,你能否办到?如果你能请分别写出这个方框中的最大数和最小数.
A 当这九个数的和是2007时,能否办到,如果能方框中最大数是 ,最小数是 ;
B当这九个数的和是2008时,能否办到,如果能方框中最大数是?最小数是?
27.(5分)日历的规律:认真观察如图阴影方框中正中间的数与其他4个数的关系.
(1)中间数是x,则左边的数是x﹣1,右边的数是x+1,上面的数是 ,下面的数是 .
(2)方框中5个数之和与该方框中间的数有什幺关系?
(3)当5个数的和是80时,中间的数是多少?
28.(5分)仔细观察如图,任意框出四个数,请将表格中其余三个数用含有字母的式子表示出来.
如果框出的四个数的和是84,那么这四个数分别是多少?
29.(6分)表中一共有50个奇数,黑线框出的5个数之和是115;仔细观察后回答问题.
(1)你能发现每次框出的5个数的和与中间数有什么关系吗?
(2)如果框出5个数的和要是375,应该怎么框?(先在图中框一框,并在下面用文字说明)
(3)能框出和是295的5个数吗?为什么?
(4)一共可以框出多少个大小不同的和?
30.(5分)下表中粗线框中三个数的和是9.在表中移动这个粗线框,可以使每次框出的三个数的和各不相同.
(1)一共可以框出多少个不同的和?
(2)能框出和是64的三个数吗?为什么?
31.(6分)探索与实践:认真观察月历表的规律,如图阴影方框中正中间的数与其他四个数的关系.
(1)正中间的数是y,左边的数是 ,右边的数是 ,上面的数是 ,下面的数是 .
(2)方框中5个数之和与该方框正中间的数有什么关系?
(3)当5个数的和是115时,正中间的数是 .
32.(6分)如图是一张4×4的方格图,它由16个小正方形组成,每个小正方形里都写了一个数.
(1)在这个方格图上框出形,那么框出的4个数的和一共有多少种?其中和最大是多少?最小呢?
(2)在这个方格图上框出形,那么框出的5个数的和一共有多少种?每5个数的和一定是15的倍数吗?为什么?
参考答案与试题解析
一.选择题(共10小题,满分20分,每小题2分)
1.解:通过观察与想象知道该模型共由9个小正方体拼成.
即3+2+1+1+2=9(个).
故选:B.
2.解:给这10张如愿券编号为1~10,
只有第9、10号不能放在开头,所以一共有:
10﹣2=8(种);
答:共有8种不同的拿法.
故选:C.
3.解:3a+3a+2a×3=12a,
答:这个图形的周长是12a.
故选:D.
4.解:数字数:13﹣2+1=12(个)
不同的和数:12﹣2+1=11(个)
答:一共有11种不同的和.
故选:B.
5.解:相邻的4个数有15﹣4+1=12种情况,
则有12种不同的和,即一共有12种不同的框法.
故选:C.
6.解:观察图形可知:中间数只能在第二、三、四行,而且中间数的上下左右必须有数,那么:
第二行的中间数可以是:8,9,10,11;
第三行的中间数可以是:14,15,16,17,18;
第四行的中间数可以是:21;
一共有4+5+1=10(个);
有10个不同的中间数,就有10个不同的和.
故选:C.
7.解:由分析得出:不同的框法有:6×4=24(种).
答:一共有24种不同的框法.
故选:C.
8.解:31﹣2=29(个).
答:共可得到29个不同的和.
故选:C.
9.解:10﹣1=9(中);
答:一共可以得到9个不同的和.
故选:D.
10.解:根据题干分析可得:14+23+32=69
答:这三个数字之和可能是69.
故选:A.
二.填空题(共9小题,满分12分)
11.解:因为像这种形式五个数的和是105,
那么五个数的和是中间的数的5倍,
所以中间的数是:105÷5=21,
即中间的那个数是21.
故答案为:21.
12.解:40﹣2+1﹣3
=39﹣3
=36
故共可得到36个不同的和.
故答案为:36.
13.解:29+30+31
=59+31
=90
1+5×4=21(种)
答:框出的3个数和最大的是 90,一共可以框出 21种不同的和.
故答案为:90,21.
14.解:依次选出4个连续的数可以为:1、2、3、4; 2、3、4、5; 3、4、5、6; 4、5、6、7; 5、6、7、8.
所以每次选出4个连续的数求和,一共可以有5种不同的和.
故答案为:5.
15.解:8﹣2=6(种)
答:一共有6种不同的剪法.
故答案为:6种.
16.解:贴法如下图:
(11﹣3+1)×(6﹣2+1)
=9×5
=45(种)
答:在保持组合图案不变的情况下,有45种不同的贴法.
故答案为:6,45.
17.解:明明可以选择以下的两天去旅游:
10月1日和10月2日;10月2日和10月3日;10月3日和0月4日;10月4日和10月5日;10月5日和10月6日;10月6日和10月7日;共6种选择.
故答案为:6种.
18.解:根据题干分析可得:
(1)如果每次框出2个数,可以得到9个不同的和.
(2)如果每次框出3个数,可以得到8个不同的和.
故答案为:9,8.
19.解:15﹣4+1=12(种);
答:一共有12种不同的涂法.
故答案为:12.
三.操作题(共6小题,满分30分,每小题5分)
20.解:(1)5和4是互质数,所以5和4的最小公倍数是:5×4=20,
所以5月2日,他们同时休息,那么下一次他们同时休息是:2+20=22,即5月22日,星期六;
(2)上表中被阴影覆盖的5个数和是:11+17+18+19+25=90;
90÷18=5,所以这5个数的和是中间的数的5倍;
(3)因为这5个数的和是中间的数的5倍,所以中间数是75÷5=15,则框出的5个数为:8、14、15、16、22;
如图:
(4)1+5×2=11(个)
所以,一共可以框出11个不同的和.
故答案为:六、11.
21.解:(1)1+7+8+9+15=40=8×5
2+8+9+10+16=45=9×5
3+9+10+11+17=50=10×5
所以可得:框出的5个数的和是中间数的5倍.
(2)90÷5=18
答:x的值是18;
故答案为:5,18.
22.解:31由圆和平行四边形组成,且圆大,平行四边形小,如图:
23.解:根据图形的旋转规律,如图:
24.解:(1)48÷3=16,这三个数分别是15、16、17(用红色长方形框出).
(2)99÷3÷3=11,即这九个数中间的一个数是11,这九个分别是:3、4、5、10、11、12、17、18、19(用绿色正方形框出).
25.解:(1)29+30+31=90
1+2+3=6
2+5+5+5+4=21(种)
答:框出的3个数和最大的是90,最小是6,一共可以框出21种不同的和.
(2)87÷3=29,中间的数是29,前一个数是28,后一个数是30,所以:
故答案为:90,6,21.
四.解答题(共7小题,满分38分)
26.解:设方框内最小的数(左上角)为a,则框内的九个数可分别表示为:a,a+1,a+2,a+7,a+7+1,a+7+2,a+7×2,a+7×2+1,a+7×2+2.
它们的和是9a+7×3+7×2×3+(1+2)×3=9×(a+8).
由于总和9×(a+8)是9的倍数,
所以总和是2008不可能,只可能是2007.
当方框内9个数的和是2007时,框内的最小数是2007÷9﹣8=215,最大数是215+7×2+2=231;
答:方框中的最大数是231,最小数是215.
故答案为:231,215.
27.解:(1)由分析得出:中间数是x,则左边的数是x﹣1,右边的数是x+1,上面的数是x﹣7,下面的数是x+7;
(2)左边五个数的和是:7+13+14+15+21=70,70是中间的数14的5倍;右边五个数的和是:4+10+11+12+18=55,55是中间的数11的5倍;
所以得出:方框中5个数之和是该方框中间的数的5倍;
(3)中间的数都是:80÷5=16.
答:中间的数是16.
故答案为:(1)x﹣7;x+7;(2)方框中5个数之和是该方框中间的数的5倍;(3)中间的数是16.
28.解:
因为17+18+24+25=84,所以这四个数分别是17、18、24、25.
29.解:(1)通过每次框出的5个数,发现:115÷23=5倍,所以5个数之和正好是中间数的5倍;
(2)375÷5=75,框出的5个数的中间的数是75,所以框法为:
(3)295÷5=59
因为59在所给表的最右边,不能被框为中间的数,
所以,不能框出和是295的5个数;
(4)根据所给框的例子,知道23、25、27、29、31、33、35、37、及它们对应的下两行的数,都可以被框为中间的数,
所以,一共可以框出大小不同的和的个数:8×3=24(个).
答:一共可以框出24个大小不同的和.
30.解:(1)1﹣29共有15个数字,每次框出3个数字,一共有15﹣2=13(种)框法,所以有13个不同的和.
答:一共可以框出13个不同的和.
(2)由题意可知框出的三个数的和是3的倍数,因为64不是3的倍数,所以不能框出和是64的三个数.
答:不能框出和是64的三个数.因为框出的三个数的和是3的倍数,因为64不是3的倍,所以不能框出和是64的三个是.
31.解:(1)由分析得出:
中间数是x,则左边的数是x﹣1,右边的数是x+1,上面的数是x﹣7,下面的数是x+7;
(2)左边五个数的和是:7+13+14+15+21=70,70是中间的数14的5倍;右边五个数的和是:4+10+11+12+18=55,55是中间的数11的5倍;
所以得出:方框中5个数之和是该方框中间的数的5倍
答:方框中5个数之和是该方框中间的数的5倍.
(3)中间的数都是:115÷5=23.
答:当5个数的和是115时,正中间的数是23.
故答案为:(1)y﹣1,y+1,y﹣7;y+7.
32.解:(1)竖着有3种框法,横着有2种框法,
一共有3×2=6种,即出的4个数的和一共有6种;
最大是30+42+45+48=165
最小是3+15+18+21=57
(2)横着有2种框法,竖着也有2种框法,一共有2×2=4种框法,框出的5个数的和一共有4种;
根据框中心数与周围数的关系,可得和是中心数的5倍,中心的数18、21、30、33都是3的整数倍,5×3=15,所以每5个数的和一定是15的倍数.
