青岛版七年级数学上册第1章 基本的几何图形1.4 线段的比较与作法课件(第一课时 共19张)
文档属性
| 名称 | 青岛版七年级数学上册第1章 基本的几何图形1.4 线段的比较与作法课件(第一课时 共19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 485.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-10 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
1.4线段的比较(第一课时)
学习目标
1、会比较两条线段的大小。
2、掌握线段的基本性质(线段公理)。
3、理解两点间的距离的意义。
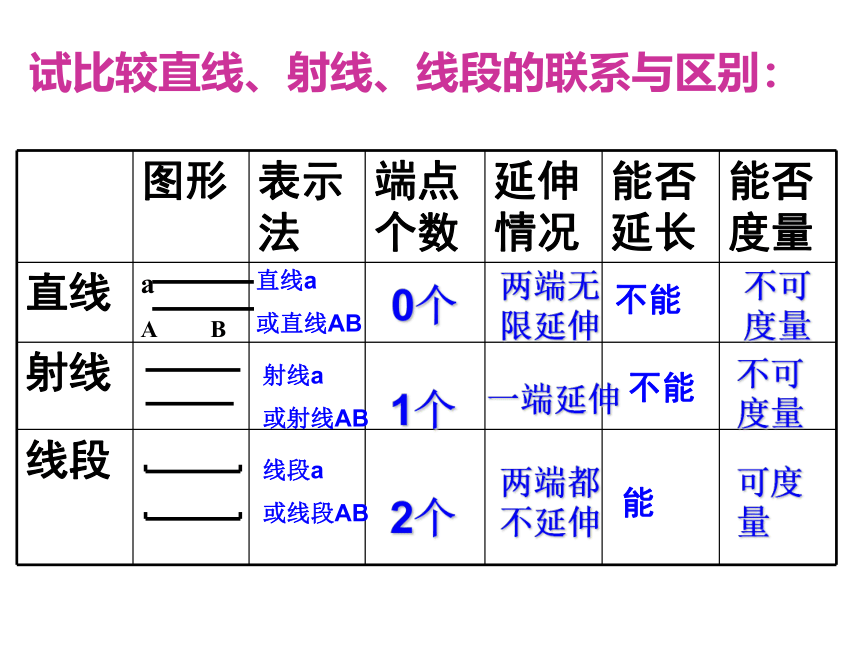
试比较直线、射线、线段的联系与区别:
射线a
或射线AB
直线a
或直线AB
线段a
或线段AB
0个
1个
2个
两端无
限延伸
一端延伸
两端都
不延伸
不可度量
不可度量
可度量
不能
不能
能
图形 表示法 端点个数 延伸情况 能否延长 能否度量
直线
射线
线段
问题:
能否量出直线、射线、线段的长度?
怎么量出线段的长度?
怎么比较两条线段的长度?
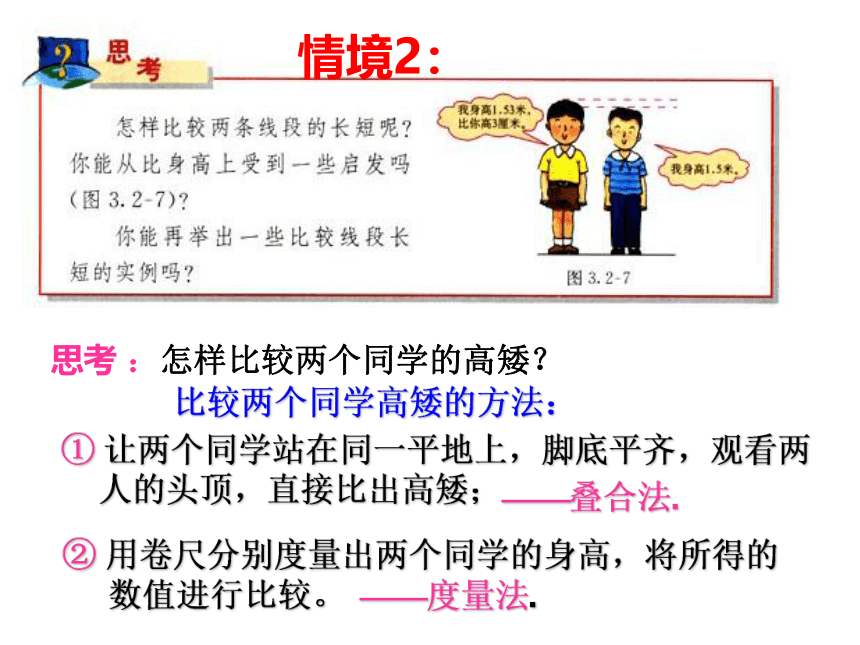
思考 :怎样比较两个同学的高矮?
比较两个同学高矮的方法:
——叠合法.
① 让两个同学站在同一平地上,脚底平齐,观看两
人的头顶,直接比出高矮;
② 用卷尺分别度量出两个同学的身高,将所得的
数值进行比较。
——度量法.
情境2:
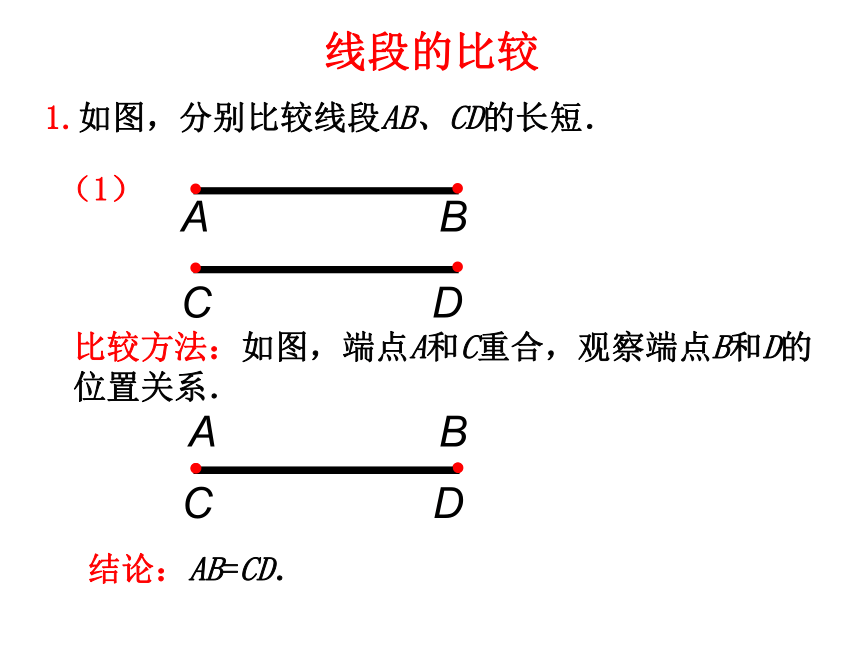
线段的比较
1.如图,分别比较线段AB、CD的长短.
比较方法:如图,端点A和C重合,观察端点B和D的位置关系.
结论:AB=CD.
(1)
比较方法:如图,端点A和C重合,观察端点B和D的位置关系.
结论:AB>CD.
(2)
比较方法:如图,端点A和C重合,观察端点B和D的位置关系.
结论:AB(3)
2.用刻度尺度量一条线段的长度的方法:
问题1:你能不能根据上述方法,再给出一种比较两条线段的大小的方法?
问题2:如图,用两种方法比较线段m和n的大小?
A、B两地之间有不同的路线可走,如果从A地尽快赶往B地,你会选择哪条路线?
选择直路,不走曲折的路
线段基本性质:
两点间的所有连线中,线段最短.
简写:两点之间,线段最短.
两点之间线段的长度,叫做这两点间的距离.
“两点之间的线段”和“两点间的距离”有何区别?
两点之间的线段是图形.
两点之间线段的长度才是两点的距离,它是一个数量, 且有长度单位.
因此不能说线段是距离.
在学校400米环形跑道进行田径赛,田径赛中的200米跑,是指跑道的起点到终点的距离是200米吗?
不对.因为200米不是起点到终点的线段的长,而是曲线跑道的长.
理解强化
a
a
b
b
AC
BC
AB
BC
AB
AC
4、_____ ,叫做两点间的距离.
5、如图,从A地到B地的四条路中,最近的一条是___. 理由是_______.
小结:本节课我们主要学习了
3、线段的基本性质(线段公理);
4、两点间的距离。
【测测试试】1、按下列度量结果,问A、B、C三点能在同一条直线上吗?
(1)AB=8cm,BC=4cm,AC=12cm
(2)AB=10cm,BC=2cm,AC=7cm
(3)AB=11cm,BC=5cm,AC=6cm
解: (1)如图, ∵AB+BC=8+4=12(cm)
又∵AC=12cm
∴ AB+BC=AC
∴A、B、C三点在同一条直线上.
(2)如图, ∵AC=AB-BC=10-2=8(cm)
又∵AC=7cm
∴A、B、C三点不在同一条直线上.
(2)AB=10cm,BC=2cm,AC=7cm
(3)AB=11cm,BC=5cm,AC=6cm
(3)如图, ∵AB-BC=11-5=6(cm)
又∵AC=6cm
∴ AB-BC=AC
∴A、B、C三点在同一条直线上.
∴AC的值与已知不符合
2、已知线段AB=18cm,点C是任意一点,求AC+BC的最小值.
解:如图,
∵当点C在线段AB外时,根据线段基本性质,
都有AC+BC>AB
又∵当点C在线段AB上时,
都有AC+BC=AB
∴当点C在线段AB上时,AC+BC的值最小,
这时AC+BC=AB=18cm
∴AC+BC的最小值是18cm.
3. (如图)画线段AB=8cm,CD=6cm,使AB、CD互相平分于点O,连结AC、BD,用圆规比较线段AC和BD的大小,说出你所得的结论.
4、如图,在直角三角形ABC中,指出最长的边并说明理由.
A
B
C
1.4线段的比较(第一课时)
学习目标
1、会比较两条线段的大小。
2、掌握线段的基本性质(线段公理)。
3、理解两点间的距离的意义。
试比较直线、射线、线段的联系与区别:
射线a
或射线AB
直线a
或直线AB
线段a
或线段AB
0个
1个
2个
两端无
限延伸
一端延伸
两端都
不延伸
不可度量
不可度量
可度量
不能
不能
能
图形 表示法 端点个数 延伸情况 能否延长 能否度量
直线
射线
线段
问题:
能否量出直线、射线、线段的长度?
怎么量出线段的长度?
怎么比较两条线段的长度?
思考 :怎样比较两个同学的高矮?
比较两个同学高矮的方法:
——叠合法.
① 让两个同学站在同一平地上,脚底平齐,观看两
人的头顶,直接比出高矮;
② 用卷尺分别度量出两个同学的身高,将所得的
数值进行比较。
——度量法.
情境2:
线段的比较
1.如图,分别比较线段AB、CD的长短.
比较方法:如图,端点A和C重合,观察端点B和D的位置关系.
结论:AB=CD.
(1)
比较方法:如图,端点A和C重合,观察端点B和D的位置关系.
结论:AB>CD.
(2)
比较方法:如图,端点A和C重合,观察端点B和D的位置关系.
结论:AB
2.用刻度尺度量一条线段的长度的方法:
问题1:你能不能根据上述方法,再给出一种比较两条线段的大小的方法?
问题2:如图,用两种方法比较线段m和n的大小?
A、B两地之间有不同的路线可走,如果从A地尽快赶往B地,你会选择哪条路线?
选择直路,不走曲折的路
线段基本性质:
两点间的所有连线中,线段最短.
简写:两点之间,线段最短.
两点之间线段的长度,叫做这两点间的距离.
“两点之间的线段”和“两点间的距离”有何区别?
两点之间的线段是图形.
两点之间线段的长度才是两点的距离,它是一个数量, 且有长度单位.
因此不能说线段是距离.
在学校400米环形跑道进行田径赛,田径赛中的200米跑,是指跑道的起点到终点的距离是200米吗?
不对.因为200米不是起点到终点的线段的长,而是曲线跑道的长.
理解强化
a
a
b
b
AC
BC
AB
BC
AB
AC
4、_____ ,叫做两点间的距离.
5、如图,从A地到B地的四条路中,最近的一条是___. 理由是_______.
小结:本节课我们主要学习了
3、线段的基本性质(线段公理);
4、两点间的距离。
【测测试试】1、按下列度量结果,问A、B、C三点能在同一条直线上吗?
(1)AB=8cm,BC=4cm,AC=12cm
(2)AB=10cm,BC=2cm,AC=7cm
(3)AB=11cm,BC=5cm,AC=6cm
解: (1)如图, ∵AB+BC=8+4=12(cm)
又∵AC=12cm
∴ AB+BC=AC
∴A、B、C三点在同一条直线上.
(2)如图, ∵AC=AB-BC=10-2=8(cm)
又∵AC=7cm
∴A、B、C三点不在同一条直线上.
(2)AB=10cm,BC=2cm,AC=7cm
(3)AB=11cm,BC=5cm,AC=6cm
(3)如图, ∵AB-BC=11-5=6(cm)
又∵AC=6cm
∴ AB-BC=AC
∴A、B、C三点在同一条直线上.
∴AC的值与已知不符合
2、已知线段AB=18cm,点C是任意一点,求AC+BC的最小值.
解:如图,
∵当点C在线段AB外时,根据线段基本性质,
都有AC+BC>AB
又∵当点C在线段AB上时,
都有AC+BC=AB
∴当点C在线段AB上时,AC+BC的值最小,
这时AC+BC=AB=18cm
∴AC+BC的最小值是18cm.
3. (如图)画线段AB=8cm,CD=6cm,使AB、CD互相平分于点O,连结AC、BD,用圆规比较线段AC和BD的大小,说出你所得的结论.
4、如图,在直角三角形ABC中,指出最长的边并说明理由.
A
B
C
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
