广东省佛山市南海区2019-2020学年高一上学期12月学业水平测试数学试题 扫描版含答案
文档属性
| 名称 | 广东省佛山市南海区2019-2020学年高一上学期12月学业水平测试数学试题 扫描版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 20:29:58 | ||
图片预览



文档简介
南海区2022届高一学业水平测试
高一数学参考答案
单项选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号
1
2
3
4
5
6
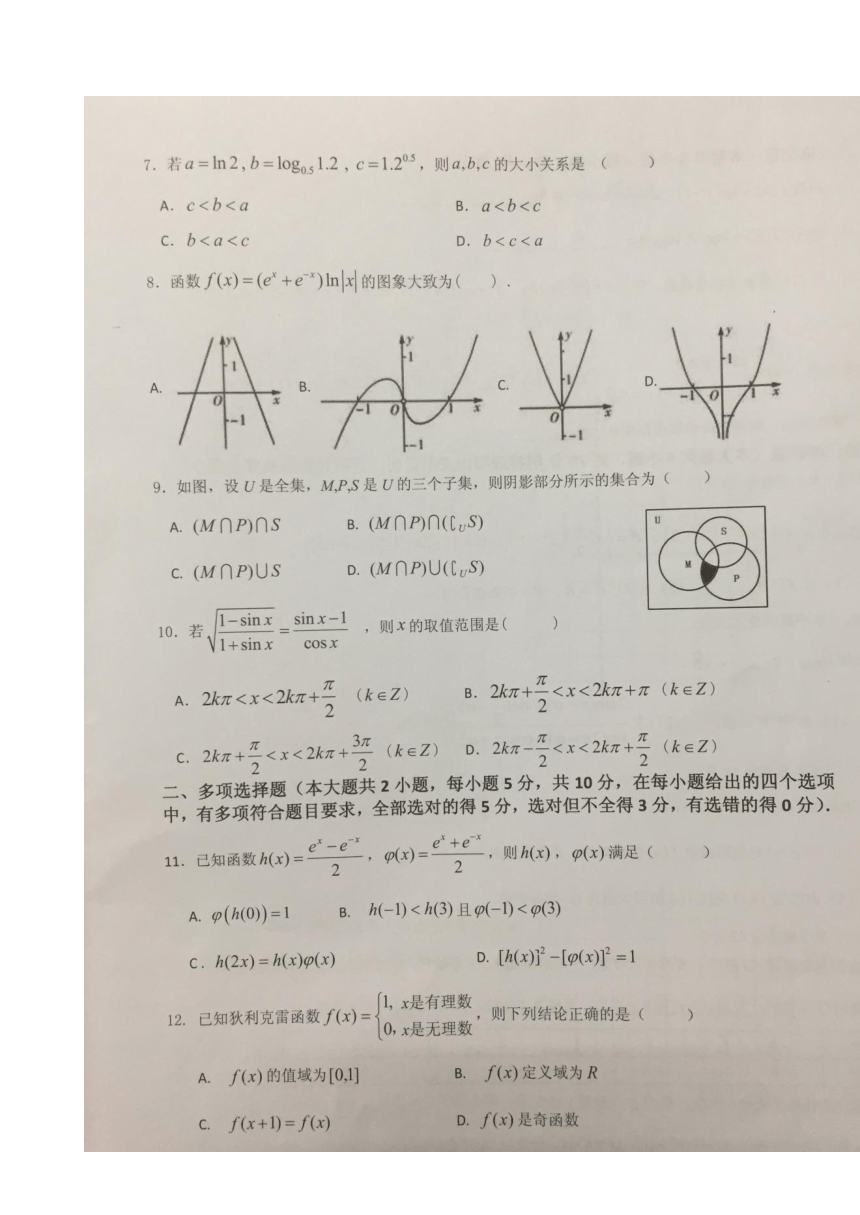
7
8
9
10
答案
A
A
A
B
D
B
C
D
B
C
二、多项选择题(本大题共2小题,每小题5分,共10分,在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,选对但不全得3分,有选错的得0分)
11.AB 12. BC
三、填空题(本题共4小题,每小题5分,共20分.第16题第1小问2分,第2小问3分)
13. 14. 15. 16. 1,
四、解答题(本题共6小题,第17题10分,第18--22题每题12分,共70分)
17. (1)由题意得,………………………………………3分
又因为,所以………………………………………5分
(2)因为,所以. …………………………………………………………………6分
因为,,
所以,……………………………………………………………………………………………8分
解得,故的取值范围为.………………………………………………………10分
18. 解:(1)因为,所以,
代入可得,……………………………………2分
所以,故,,……………………………………4分
所以.…………………………………………………………………………………6分
(2)
………………………………………………………………………………10分
……………………………………………………………………………………11分
.……………………………………………………………………………12分
19. (1)的定义域为……………………………………1分
当时,…………………………………………2分
…………………………………………3分
所以且…………………………………………5分
所以当时,既不是奇函数,也不是偶函数.…………………………………………6分
(2),对称轴为………………………………………………………7分
① 当,即时,,
解得或(舍去)…………………………………………………………9分
② 当,即时,,解得或(舍去) …11分
综上:或.……………………12分
20 .解:(1)若选择函数模型,则该函数在上为单调减函数,
这与试验数据相矛盾,所以不选择该函数模型.
若选择函数模型,须,这与试验数据在时有意义矛盾,
所以不选择该函数模型.
从而只能选择函数模型,由试验数据得,………………………………………3分
,即,解得…………………………………6分
故所求函数解析式为:.……………………………………7分
(2)设超级快艇在AB段的航行费用为y(万元),
则所需时间为(小时),其中,
结合(1)知,……………………………………9分
所以当时,.…………………………………………………………………………11分
答:当该超级快艇以1百公里/小时航行时可使AB段的航行费用最少,且最少航行费用为2.1万元.……………………………………………………………………………………………………12分
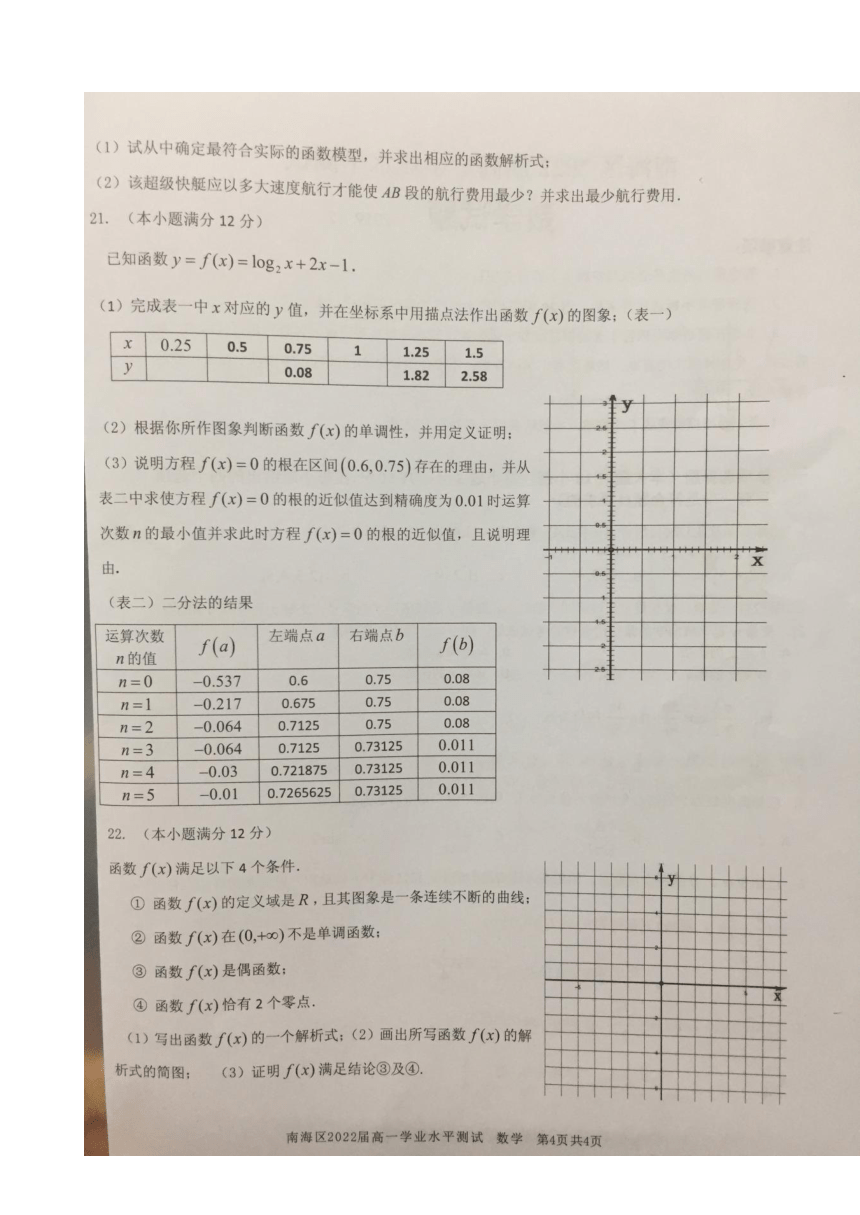
21. 解:(1)
0.5
0.75
1
1.25
1.5
0.08
1
1.82
2.58
……………………4分
(2)函数在定义域内为增函数,证明:设,则,,因为
即所以函数在定义域内为增函数. ……………………………………………………………………………………8分
(3)
是图象是一条连续不断的曲线,…………………………………9分
且…………………………………10分
当时,所以当时方程的根的近似值达不到精确度为
当时,所以当时方程的根的近似值达到精确度为,所以…………………………………11分
方程的根的近似值为.…………………………………12分
22 . 本题为开放性题,答案不唯一,只需写出符合条件的函数即可,提供以下5个函数仅供参考,写出函数给4分,作图2分,证明满足结论③及④每个3分.
(1) (2)
(3) (4)
(5)
下面以函数为例给出证明:
证明:的定义域为R
因为对定义域的每一个,都有
,
所以函数是偶函数,……………………………………………………………9分
又因为当时,
解得
所以当时,函数只有一个零点,
又因为函数是偶函数,
所以函数恰有2个零点.………………………………………………………………………12分
同课章节目录
