人教版九年级下册第二十六章反比例函数:26.1.2 第1课时 反比例函数的图象和性质 课件(22张ppt)
文档属性
| 名称 | 人教版九年级下册第二十六章反比例函数:26.1.2 第1课时 反比例函数的图象和性质 课件(22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 14:19:13 | ||
图片预览





文档简介
(共22张PPT)
26.1.2 反比例函数的图象和性质
第二十六章 反比例函数
导入新课
讲授新课
当堂练习
课堂小结
第1课时 反比例函数的图象和性质
学习目标
观察与思考
导入新课
讲授新课
解析:画函数的图象步骤一般分为:
列表
描点
连线
三个步骤,需要注意的是在反比例函数中自变量x不能为0.
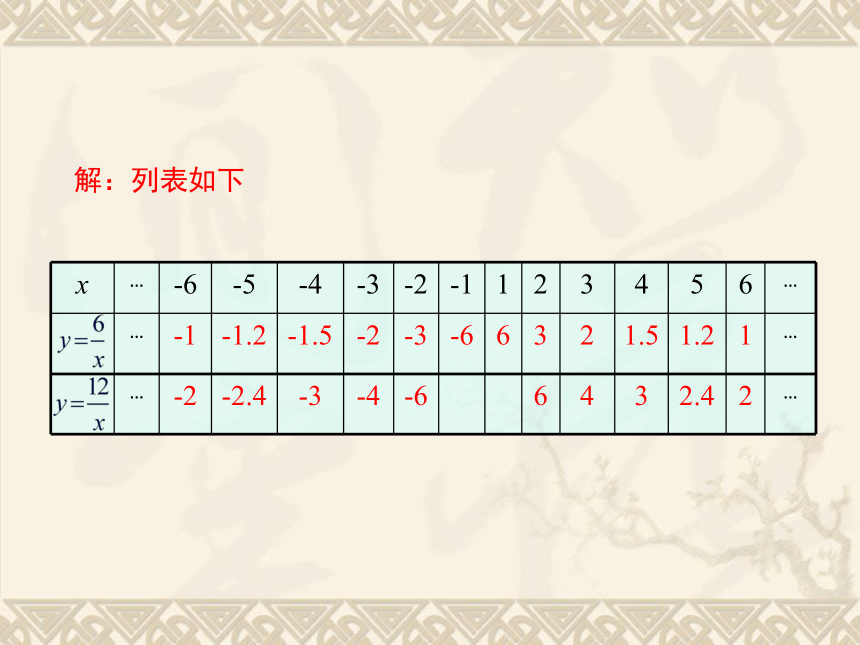
解:列表如下
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… -1 -1.2 -1.5 -2 -3 -6 6 3 2 1.5 1.2 1 …
…
-2 -2.4 -3 -4 -6 6 4 3 2.4 2 …
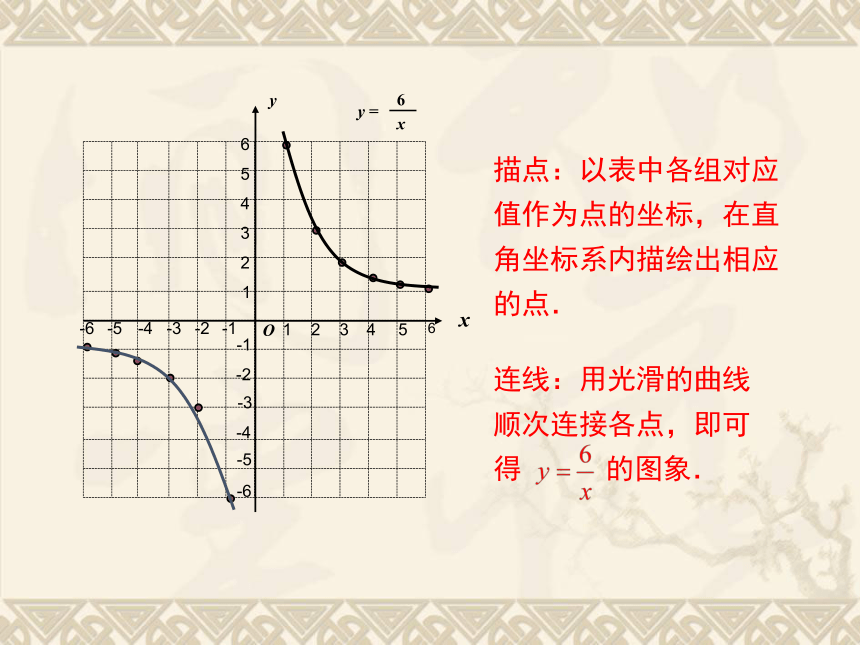
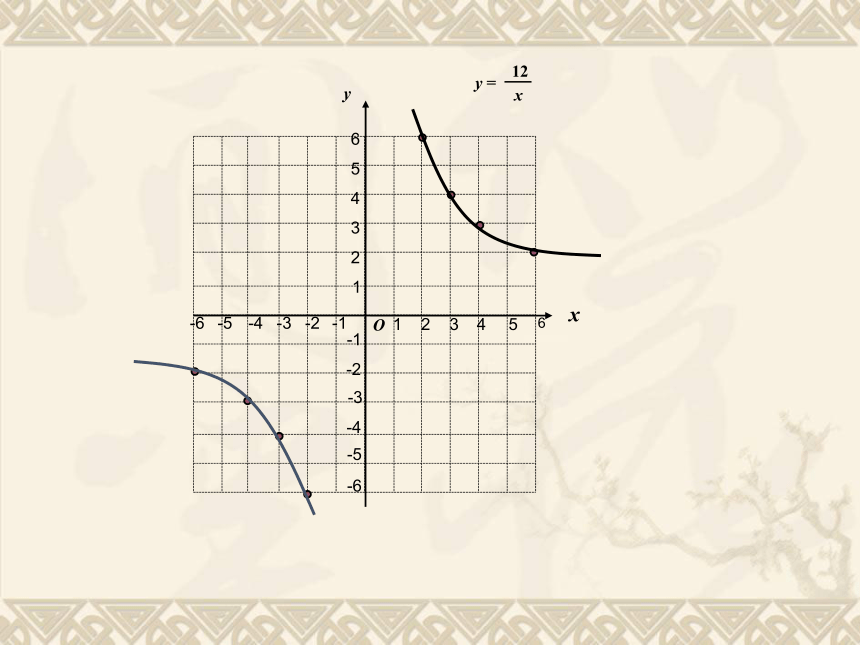
描点:以表中各组对应值作为点的坐标,在直角坐标系内描绘出相应的点.
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
-6
-5
5
6
x
y
O
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
-6
-5
5
6
x
O
y
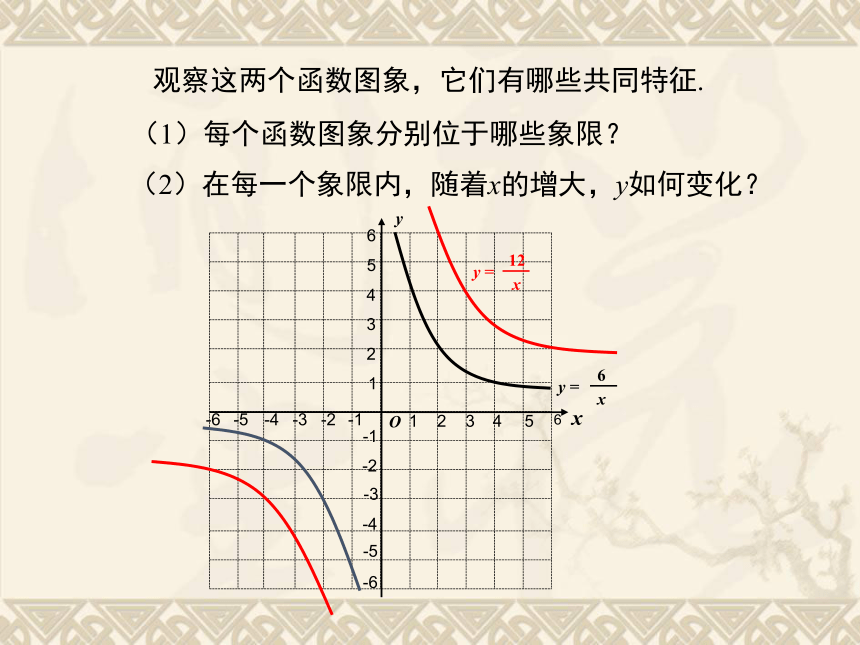
观察这两个函数图象,它们有哪些共同特征.
(1)每个函数图象分别位于哪些象限?
(2)在每一个象限内,随着x的增大,y如何变化?
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
-6
-5
5
6
x
O
y
图象
性质
由两条曲线组成,且分别位于第一、三象限
它们与x轴、y轴都不相交
在每个象限内,y随x的增大而减小
总结归纳
C
练一练
C
典例精析
当k=-2, -4 , -6时,反比例函数 的图象,有哪些共同特征?
y
y
y
x
x
x
O
O
O
观察与思考
图象
性质
由两条曲线组成,且分别位于第二、四象限
它们与x轴、y轴都不相交
在每个象限内,y随x的增大而增大
总结归纳
<
解析:由题意知该反比例函数位于第二、四象限,且y随着自变量x的增大而增大,故 y1 < y2.
例3.已知反比例函数 ,y随x的增大而增大,求a的值.
解:由题意得a2+a-7=-1,且a-1<0.
解得a=-3.
解:(1)∵反比例函数 (k为常数,k≠0)的图象经过点
A(2,3),
∴把点A的坐标代入表达式,得 ,
解得k=6,
∴这个函数的表达式为 .
(2)∵反比例函数的表达式为 ,
∴6=xy
分别把点B,C的坐标代入,得(-1)×6=-6≠6,则
点B不在该函数图象上,
3×2=6,则点C在该函数图象上.
(3)∵当x=-3时,y=-2;当x=-1时,y=-6,且
k>0,
∴当x<0时,y随x的增大而减小,
∴当-3(1)(3)
当堂练习
<
3.在反比例函数 (k>0)的图象上有两点A( x1 , y1 ),
B( x2 , y2 ) 且x1>x2>0,则y1-y2 0.
图象位于第一、三象限
图象位于第二、四象限
在每个象限内,y随x的增大而减小
在每个象限内,y随x的增大而增大
课堂小结
反比例函数
k k>0 k<0
图象
性质
课后作业
26.1.2 反比例函数的图象和性质
第二十六章 反比例函数
导入新课
讲授新课
当堂练习
课堂小结
第1课时 反比例函数的图象和性质
学习目标
观察与思考
导入新课
讲授新课
解析:画函数的图象步骤一般分为:
列表
描点
连线
三个步骤,需要注意的是在反比例函数中自变量x不能为0.
解:列表如下
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… -1 -1.2 -1.5 -2 -3 -6 6 3 2 1.5 1.2 1 …
…
-2 -2.4 -3 -4 -6 6 4 3 2.4 2 …
描点:以表中各组对应值作为点的坐标,在直角坐标系内描绘出相应的点.
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
-6
-5
5
6
x
y
O
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
-6
-5
5
6
x
O
y
观察这两个函数图象,它们有哪些共同特征.
(1)每个函数图象分别位于哪些象限?
(2)在每一个象限内,随着x的增大,y如何变化?
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
-6
-5
5
6
x
O
y
图象
性质
由两条曲线组成,且分别位于第一、三象限
它们与x轴、y轴都不相交
在每个象限内,y随x的增大而减小
总结归纳
C
练一练
C
典例精析
当k=-2, -4 , -6时,反比例函数 的图象,有哪些共同特征?
y
y
y
x
x
x
O
O
O
观察与思考
图象
性质
由两条曲线组成,且分别位于第二、四象限
它们与x轴、y轴都不相交
在每个象限内,y随x的增大而增大
总结归纳
<
解析:由题意知该反比例函数位于第二、四象限,且y随着自变量x的增大而增大,故 y1 < y2.
例3.已知反比例函数 ,y随x的增大而增大,求a的值.
解:由题意得a2+a-7=-1,且a-1<0.
解得a=-3.
解:(1)∵反比例函数 (k为常数,k≠0)的图象经过点
A(2,3),
∴把点A的坐标代入表达式,得 ,
解得k=6,
∴这个函数的表达式为 .
(2)∵反比例函数的表达式为 ,
∴6=xy
分别把点B,C的坐标代入,得(-1)×6=-6≠6,则
点B不在该函数图象上,
3×2=6,则点C在该函数图象上.
(3)∵当x=-3时,y=-2;当x=-1时,y=-6,且
k>0,
∴当x<0时,y随x的增大而减小,
∴当-3
当堂练习
<
3.在反比例函数 (k>0)的图象上有两点A( x1 , y1 ),
B( x2 , y2 ) 且x1>x2>0,则y1-y2 0.
图象位于第一、三象限
图象位于第二、四象限
在每个象限内,y随x的增大而减小
在每个象限内,y随x的增大而增大
课堂小结
反比例函数
k k>0 k<0
图象
性质
课后作业
