人教版数学七年级上册第四章几何图形初步: 4.3.2 角的比较与运算同步测试(含答案)
文档属性
| 名称 | 人教版数学七年级上册第四章几何图形初步: 4.3.2 角的比较与运算同步测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 256.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-09 00:00:00 | ||
图片预览


文档简介
2019年秋人教版七年级上册数学 第四章4.3.2角的比较与运算 课后练习
一、单选题
1.已知∠A=18°20′36″,∠B=18.35°,∠C=18°21′,下列比较正确的是( )
A.∠A<∠B B.∠B<∠A C.∠B<∠C D.∠C<∠B
2.如图,在∠AOB的内部取一点C,在∠AOB的外部取一点D,作射线OC,OD.下列结论错误的是( )
A.∠AOB<∠AOD B.∠BOC<∠AOB C.∠COD>∠AOD D.∠AOB>∠AOC
3.已知射线OC是∠AOB的平分线,若∠AOC=30°,则∠AOB的度数为( )
A. B. C. D.
4..如图,已知O是直线上一点,,平分,的度数是( )
A. B. C. D.
5.下列说法正确的是( )
A.12°25′+25°47′=39°2′ B.48°15′﹣30°30′=18°15′
C.58.25°=58°15′ D.42°24′<42.34°
6.借助一副三角尺,不能画出下面哪个度数的角( )
A. B. C. D.
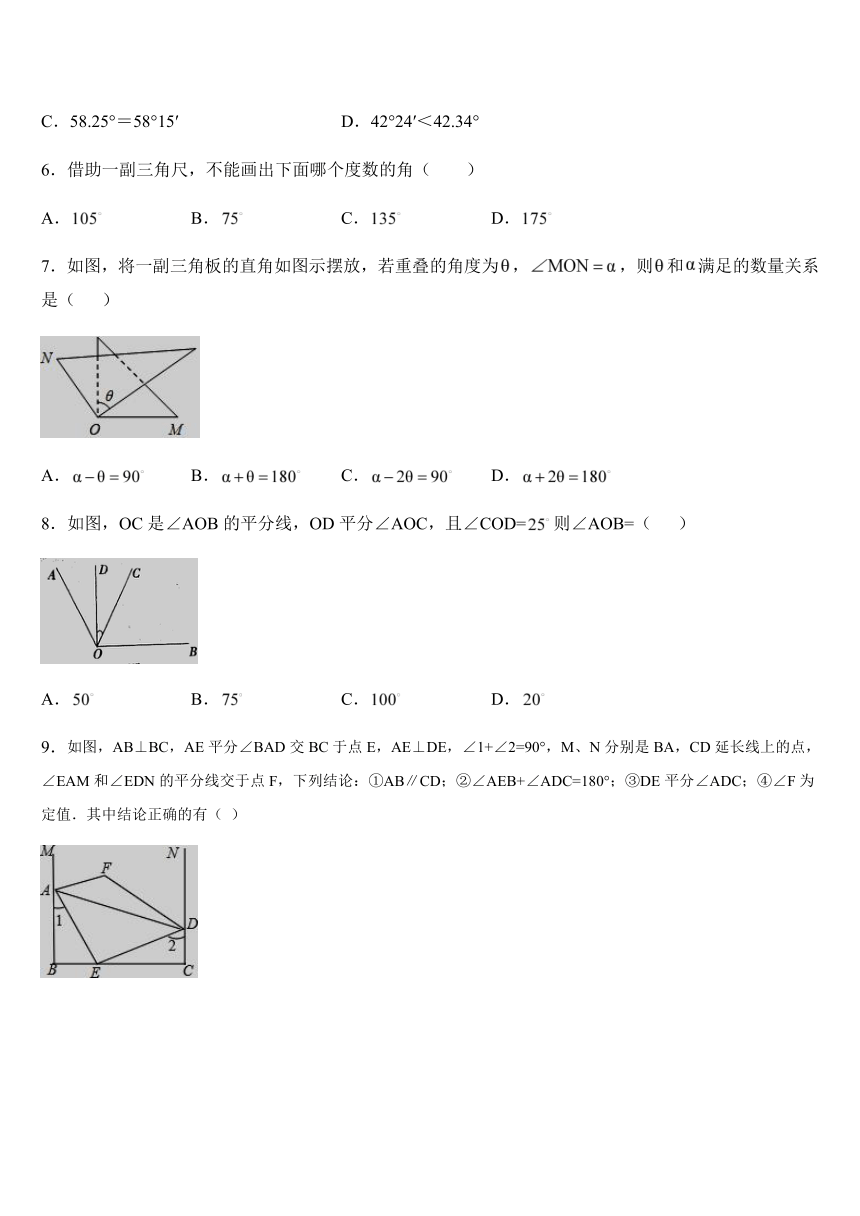
7.如图,将一副三角板的直角如图示摆放,若重叠的角度为,,则和满足的数量关系是( )
A. B. C. D.
8.如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=则∠AOB=( )
A. B. C. D.
9.如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F,下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值.其中结论正确的有( )
A.4个 B.1个 C.2个 D.3个
二、填空题
10.计算:67°33′﹣48°39′=_____.
11.如图,∠AOB=72°32′,射线OC在∠AOB内,∠BOC=30°40′,则∠AOC=_____.
12.如图,点A,O,B在一条直线上,OE平分∠BOC,OF平分∠AOC,则∠EOF=_____.
13.以∠AOB的顶点O为端点引射线OC,使∠AOC:∠BOC=5:4,若∠AOB=27°,则∠AOC=______.
14.如图,已知OM,ON分别是∠BOC和∠AOC的角平分线,∠AOB=86°,(1)∠MON=______(度);(2)当OC在∠AOB内绕点O转动时,∠MON的值______改变(填“会”或“不会”).
三、解答题
15.如图所示,回答下列问题:
(1)比较∠FOD与∠FOE的大小;
(2)借助三角板比较∠DOE与∠BOF的大小;
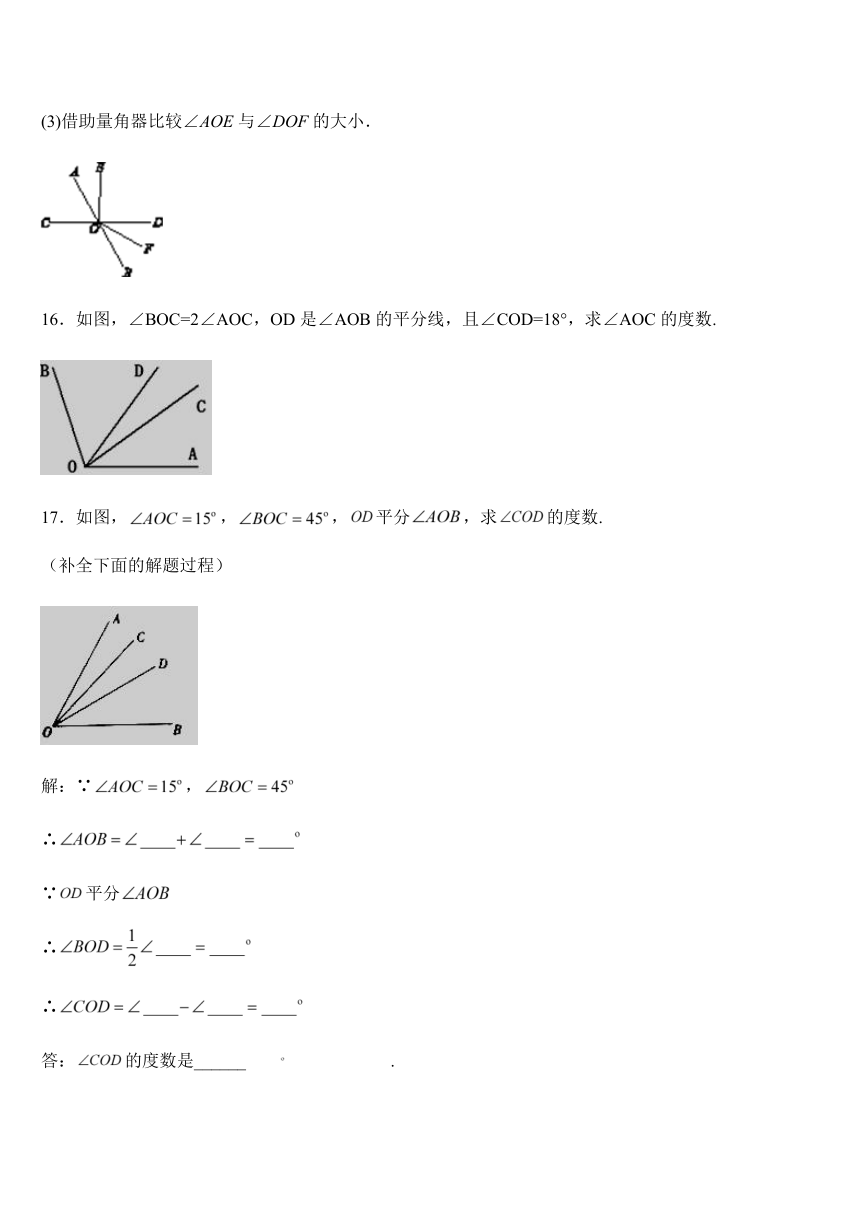
(3)借助量角器比较∠AOE与∠DOF的大小.
16.如图,∠BOC=2∠AOC,OD是∠AOB的平分线,且∠COD=18°,求∠AOC的度数.
17.如图,,,平分,求的度数.
(补全下面的解题过程)
解:∵,
∴
∵平分
∴
∴
答:的度数是______.
18.已知:如图,直线AB、CD相交于点O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,请你过点O画直线MN⊥AB,并在直线MN上取一点F(点F与O不重合),然后直接写出∠EOF的度数.
19.以直线AB上点O为端点作射线OC,使∠BOC=63°,若∠DOE==90°,将∠DOE的顶点放在点O处.
(1)如图1,若∠DOE的边OD放在射线OB上,求∠COE的度数?
(2)如图2,将∠DOE绕点O按逆时针方向转动,使得OE平分∠AOC,说明OD是∠BOC的平分线;
(3)如图3,将∠DOE绕点O按逆时针方向转动,使得∠COD=∠AOE.求∠BOD的度数.
答案
1.A 2.A 3.D 4.D 5.C 6.D 7.B 8.C 9.D
10.18°54′ 11.41°52′ 12.90° 13.15°或135°. 14.43 不会
15.(1)∠FOD<∠FOE.(2)∠DOE>∠BOF.(3)∠AOE=∠DOF.
16. 解∵∠BOC=2∠AOC,∠BOA=∠BOC+∠AOC,
∴∠BOA=3∠AOC,
∵OD是∠AOB的平分线,
∴∠BOA=2∠AOD,
∵∠AOD=∠AOC+∠COD,∠COD=18°,
∴2(∠AOC+18°)=3∠AOC,
∴∠AOC=36°.
17.解:∵,
∴
∵平分
∴(角平分线定义)
∴
答:的度数是___15___.
18. 解:(1)∵EO⊥CD,
∴∠DOE=90°,
又∵∠BOD=∠AOC=36°,
∴∠BOE=90°-36°=54°;
(2)∵∠BOD:∠BOC=1:5,
∴∠BOD=∠COD=30°,
∴∠AOC=30°,
又∵EO⊥CD,
∴∠COE=90°,
∴∠AOE=90°+30°=120°;
(3)分两种情况:
若F在射线OM上,则∠EOF=∠BOD=30°;
若F'在射线ON上,则∠EOF'=∠DOE+∠BON-∠BOD=150°;
综上所述,∠EOF的度数为30°或150°.
19.解(1)∵∠BOE=∠COE+∠COB=90°,
又∵∠COB=63°,
∴∠COE=27°
(2)∵OE平分∠AOC,
∴∠COE=∠AOE=COA,
∵∠EOD=90°,
∴∠AOE+∠DOB=90°,∠COE+∠COD=90°,
∴∠COD=∠DOB,
∴OD所在射线是∠BOC的平分线;
(3)设∠COD=x°,则∠AOE=4x°,
①若∠COD在∠BOC的内部,
∵∠DOE=90°,∠BOC=63°,
∴4x+90﹣x+63=180,
解得:x=9
∴∠COD=9°,
∴∠BOD=63°-9°=54°
②若∠COD在∠BOC的外部,
∵∠DOE=90°,∠BOC=63°,
x+4x=180-90-63
解得:x=5.4
即∠COD=5.4°
∴∠BOD=63°+5.4°=68.4°.
∴∠BOD的度数是54°或者=68.4°
