冀教版小学六年级上册数学 第2章 比和比例 单元测试题2(有答案)
文档属性
| 名称 | 冀教版小学六年级上册数学 第2章 比和比例 单元测试题2(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 279.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-09 19:07:13 | ||
图片预览


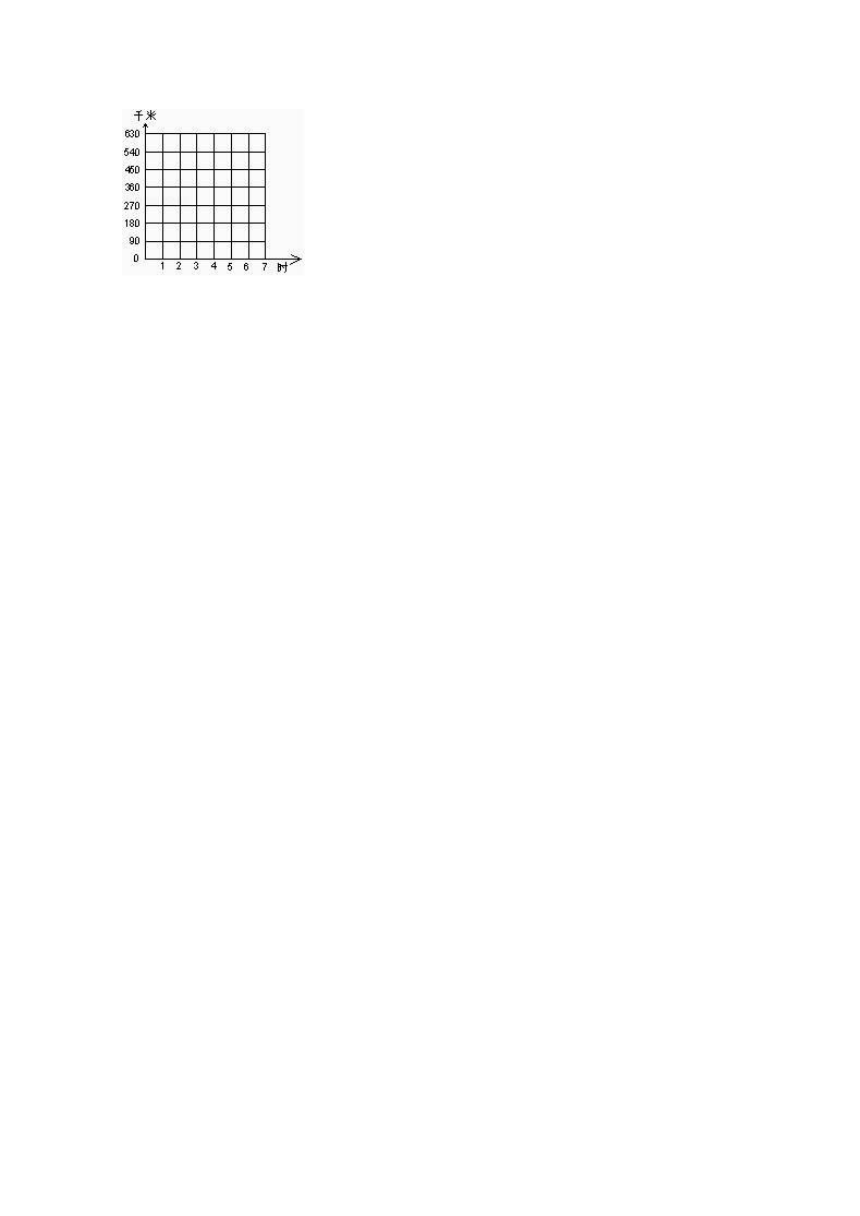

文档简介
冀教版小学六年级上册数学 第2章 比和比例 单元测试题
一.选择题(共10小题)
1.已知=1.2,=1.2,则x和y比较( )
A.x大 B.y大 C.一样大
2.下列等式中,a与b(a、b均不为0)成反比例的是( )
A.2a=5b B.a×7= C.a×=1
3.解比例:=2:1,x=( )
A.6 B.1.5 C.0.7 D.9
4.张师傅生产一个零件用小时,李师傅生产一个相同的零件用小时,张师傅与李师傅的工作效率的比为( )
A. B. C.2:3 D.3:2
5.一个比的前项是30,如果前项增加60,要使比值不变,后项应( )
A.增加60 B.减少60 C.乘3 D.除以3
6.:化简成最简整数比是( )
A. B.3:4 C.
7.下面各比中,能与:6组成比例的是( )
A.2.5:16 B.0.1: C.3:2.4 D.:4
8.8:15的前项扩大2倍,要使它的比值不变,后项应增加( )
A.扩大2倍 B.15 C.30
9.一个直角三角形,两直角边长度之和是14分米,它们的比是3:4,这个直角三角形的斜边是10分米,那么斜边上的高为( )分米.
A.7 B.8 C.10 D.4.8
10.男队与女队人数的比是3:5,那么男队人数比女队人数少( )
A. B. C. D.
二.填空题(共8小题)
11.3:4= :32
0.8:5= :15.
12.把1.2:化简是 ,比值是 .
13.=Y,XY成 比例;=Y,XY成 比例.
14.解比例:3.5:x=0.5:20%则x=
15.甲数与乙数的比例为5:3,甲数为60,乙数为 .
16.甲:乙=3:4,乙:丙=5:6,甲:乙:丙= : : .
17. ÷10=0.2= %=8: = 折.
18.已知甲乙两人年龄之差是18岁,甲乙年龄比是3:5,甲乙年龄和是 岁.
三.判断题(共5小题)
19.写同样多的作业,明明用了12分,亮亮用了15分,明明与亮亮效率的比是4:5. (判断对错)
20.2:3可以写成,也可以读成:三分之二. .(判断对错)
21.比的前项和后项都乘或减一个不为0的数,比值不变. (判断对错)
22.红花和黄花的朵数比是7:8,那么红花的朵数比黄花少. (判断对错)
23.煤的数量一定,每天的平均用煤量与使用的天数成反比例. (判断对错)
四.计算题(共1小题)
24.解比例或方程.
:=:x 0.8:x=3.75:0.75 x:=:4
(2+x):2=21:6 = x+×45=12
五.应用题(共6小题)
25.根据表中的数据,判断其中相依变化的两个量是否成正比例,并说明理由.
(1)塑料管的长度和价格.
长度/m 2 4 6 8
价格/元 40 80 120 160
(2)纸的张数和质量.
数量/张 8 16 20 28 60
质量/g 30 60 75 105 225
(3)强强的年龄和身高.
年龄/岁 2 5 8 12 18
身高/cm 85 110 137 155 174
(4)圆的直径和周长.
直径/cm 5 15 20 30
周长/cm 15.7 47.1 62.8 94.2
26.加工同一批零件,甲,乙两人的时间比是5:6,如果甲每小时加工30个,乙每小时加工多少个?
27.动物的小腿骨(胫骨)与大腿骨(股骨)的长度比值越大的动物跑得越快,
动物 盐都龙 马 羚羊
胫骨与股骨的比 59:50 23:25 5:4
根据这个结论,计算并比较三种动物中,谁跑得最快?
28.
按照这种截取的方法,笫四天截取的长度与原来木棍总长度的最简单整数比是多少?请你用喜欢的方式展示你的思考过程.
29.甲、乙两个筑路队人数的比是7:3.如果从甲队派30人到乙队,则两队的人数比就成了3:2.甲、乙两个筑路队原来各有多少人?(用比例解)
30.
时间/时 1 2 3 4 5 6 …
路程/千米 90 …
①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
②时间和路程成 比例,理由是 .
③利用图象估计一下,2.5时行 千米,行675千米需要 小时.
参考答案与试题解析
一.选择题(共10小题)
1.解:因为=1.2
x=9.6
=1.2
8=1.2y
y=6.
所以x>y.
故选:A.
2.解:A,因为2a=5b,所以=(一定),所以a、b成正比例;
B,因为a×7=,所以=14(一定),所以a、b成正比例;
C,因为a×=1,所以ab=3(一定),所以a、b成反比例;
故选:C.
3.解:=2:1
x:3=2:1
x=6.
故选:A.
4.解::=2:3;
答:张师傅与李师傅的工作效率的比为2:3.
故选:C.
5.解:一个比的前项是30,若前项增加60,可知比的前项由30变成90,相当于前项乘3,
根据比的性质,要使比值不变,后项也应该乘3;
故选:C.
6.解::、
=(×18):(×18)
=3:4(或写成分数比)
故选:BC.
7.解::6=÷6=;
A、2.5:16=2.5÷16=;
B、0.1:=0.1=;
C、3:2.4=3÷2.4=;
D、:4=÷4=;
所以能与:6组成比例的是:4;
故选:D.
8.解:8:15的前项扩大2倍,后项也扩大2倍,
8:15=16:30,
30=15+15,
即8:15的前项扩大2倍,要使它的比值不变,后项应增加15.
故选:B.
9.解:一条直角边为:14÷(3+4)×3,
=14÷7×3,
=6(分米),
另一条直角边为:14﹣6=8(分米),
设斜边上的高为x分米,
6×8÷2=10×x÷2,
10x=48,
x=48÷10,
x=4.8,
答:斜边上的高为4.8分米,
故选:D.
10.解:
(5﹣3)÷5=2÷5=
答:男队人数比女队人数少.
故选:B.
二.填空题(共8小题)
11.解:
3:4=(3×8):(4×8)=24:32
0.8:5=(0.8×3):(5×3)=2.4:15
故答案为:24,2.4.
12.解:1.2:
=(1.2×):(×)
=9:5
1.2:
=1.2÷
=
故答案为:9:5,.
13.解:因为,=Y,则X:Y=5(一定);
所以,XY成正比例;
因为,=Y,则XY=5(一定);
所以,XY成反比例.
故答案为:正,反.
14.解:3.5:x=0.5:20%
0.5x=3.5×20%
0.5x÷0.5=0.7÷0.5
x=1.4;
故答案为:1.4.
15.解:设乙数为x,
则5:3=60:x,
5x=180,
x=36.
故答案为:36.
16.解:甲:乙=3:4=(3×5):(4×5)=15:20;
乙:丙=5:6=(5×4):(6×4)=20:24;
甲:乙:丙=15:20:24;
故答案为:15,20,24.
17.解:2÷10=0.2=20%=8:40=二折.
故答案为:2,20,40,二.
18.解:18÷(5﹣3)
=18÷2
=9(岁);
9×3+9×5
=27+45
=72(岁);
答:甲乙年龄和是72岁.
故答案为:72.
三.判断题(共5小题)
19.解:(1÷12):(1÷15)
=:
=():()
=5:4;
4:5≠5:4,所以原题计算错误;
故答案为:×.
20.解:虽然2:3可以写成,但是仍读作二比三,不能读作三分之二.
因此,2:3可以写成,也可以读成:三分之二是错误的.
故答案为:×.
21.解:比的前项和后项同时乘或除以一个相同的数(0除外),比值不变;
所以原说法错误;
故答案为:×.
22.解:(8﹣7)÷8
=1÷8
=;
所以红花的朵数比黄花少;原题计算正确;
故答案为:√.
23.解:因为每天的平均用煤量×使用的天数=煤的数量(一定),
也就是两种相关联的量的乘积一定,所以,煤的数量一定,使用的天数与每天的平均用煤量成反比例.
原题说法正确.
故答案为:√.
四.计算题(共1小题)
24.解:(1):=:x
x=×
x÷=×÷
x=
(2)0.8:x=3.75:0.75
3.75x=0.8×0.75
3.75x÷3.75=0.8×0.75÷3.75
x=0.16
(3)x:=:4
4x=×
4x÷4=×÷4
x=
(4)(2+x):2=21:6
6(2+x)=21×2
6(2+x)÷6=21×2÷6
2+x=7
2+x﹣2=7﹣2
x=5
(5)=
3.5x=15×28
3.5x÷3.5=15×28÷3.5
x=120
(6)x+×45=12
x+9=12
x+9﹣9=12﹣9
x=3
x÷=3÷
x=12
五.应用题(共6小题)
25.解:(1)====20,是比值一定,所以塑料管的长度和价格成正比例.
(2)===3.75,是比值一定,所以纸的张数和质量成正比例.
(3)=42.5,=22,=17.125,比值不一定,所以强强的年龄和身高不成比例.
(4)===3.14,是比值一定,所以圆的直径和周长成正比例.
26.解:工作量一定,工作时间和工作效率成反比例关系,所以甲乙两人的工作效率比就是6:5;
30÷6×5
=5×5
=25(个)
答:乙每小时加工25个.
27.解:盐都龙:59:50═59÷50=1.18
马:23:25=23÷25=0.92
羚羊:5÷4=5÷4=1.25
1.25>1.18>0.92
答:羚羊跑得最快.
28.解:把木棍的原长设为1,则第四天截取的长度是:
×××=
第四天截取的长度:原来的长度=:1=1:16;
答:笫四天截取的长度与原来木棍总长度的最简单整数比是1:16.
29.解:设原来甲队有7x人,乙队3x人,
(7x﹣30):(3x+30)=3:2
2(7x﹣30)=3(3x﹣30)
14x﹣60=9x﹣90
5x=150
x=30
30×7=210(人)
30×3=90(人)
答:甲筑路队原来有210人,乙筑路队原来有90人.
30.解:①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
时间/时 1 2 3 4 5 6 …
路程/千米 90 180 270 360 450 540 …
②时间和路程成 正比例,理由是 路程÷时间=速度(一定).
③如图
用图象估计一下,2.5时行 225千米,行675千米需要 7.5小时.
故答案为:正,路程÷时间=速度(一定),225,7.5.
一.选择题(共10小题)
1.已知=1.2,=1.2,则x和y比较( )
A.x大 B.y大 C.一样大
2.下列等式中,a与b(a、b均不为0)成反比例的是( )
A.2a=5b B.a×7= C.a×=1
3.解比例:=2:1,x=( )
A.6 B.1.5 C.0.7 D.9
4.张师傅生产一个零件用小时,李师傅生产一个相同的零件用小时,张师傅与李师傅的工作效率的比为( )
A. B. C.2:3 D.3:2
5.一个比的前项是30,如果前项增加60,要使比值不变,后项应( )
A.增加60 B.减少60 C.乘3 D.除以3
6.:化简成最简整数比是( )
A. B.3:4 C.
7.下面各比中,能与:6组成比例的是( )
A.2.5:16 B.0.1: C.3:2.4 D.:4
8.8:15的前项扩大2倍,要使它的比值不变,后项应增加( )
A.扩大2倍 B.15 C.30
9.一个直角三角形,两直角边长度之和是14分米,它们的比是3:4,这个直角三角形的斜边是10分米,那么斜边上的高为( )分米.
A.7 B.8 C.10 D.4.8
10.男队与女队人数的比是3:5,那么男队人数比女队人数少( )
A. B. C. D.
二.填空题(共8小题)
11.3:4= :32
0.8:5= :15.
12.把1.2:化简是 ,比值是 .
13.=Y,XY成 比例;=Y,XY成 比例.
14.解比例:3.5:x=0.5:20%则x=
15.甲数与乙数的比例为5:3,甲数为60,乙数为 .
16.甲:乙=3:4,乙:丙=5:6,甲:乙:丙= : : .
17. ÷10=0.2= %=8: = 折.
18.已知甲乙两人年龄之差是18岁,甲乙年龄比是3:5,甲乙年龄和是 岁.
三.判断题(共5小题)
19.写同样多的作业,明明用了12分,亮亮用了15分,明明与亮亮效率的比是4:5. (判断对错)
20.2:3可以写成,也可以读成:三分之二. .(判断对错)
21.比的前项和后项都乘或减一个不为0的数,比值不变. (判断对错)
22.红花和黄花的朵数比是7:8,那么红花的朵数比黄花少. (判断对错)
23.煤的数量一定,每天的平均用煤量与使用的天数成反比例. (判断对错)
四.计算题(共1小题)
24.解比例或方程.
:=:x 0.8:x=3.75:0.75 x:=:4
(2+x):2=21:6 = x+×45=12
五.应用题(共6小题)
25.根据表中的数据,判断其中相依变化的两个量是否成正比例,并说明理由.
(1)塑料管的长度和价格.
长度/m 2 4 6 8
价格/元 40 80 120 160
(2)纸的张数和质量.
数量/张 8 16 20 28 60
质量/g 30 60 75 105 225
(3)强强的年龄和身高.
年龄/岁 2 5 8 12 18
身高/cm 85 110 137 155 174
(4)圆的直径和周长.
直径/cm 5 15 20 30
周长/cm 15.7 47.1 62.8 94.2
26.加工同一批零件,甲,乙两人的时间比是5:6,如果甲每小时加工30个,乙每小时加工多少个?
27.动物的小腿骨(胫骨)与大腿骨(股骨)的长度比值越大的动物跑得越快,
动物 盐都龙 马 羚羊
胫骨与股骨的比 59:50 23:25 5:4
根据这个结论,计算并比较三种动物中,谁跑得最快?
28.
按照这种截取的方法,笫四天截取的长度与原来木棍总长度的最简单整数比是多少?请你用喜欢的方式展示你的思考过程.
29.甲、乙两个筑路队人数的比是7:3.如果从甲队派30人到乙队,则两队的人数比就成了3:2.甲、乙两个筑路队原来各有多少人?(用比例解)
30.
时间/时 1 2 3 4 5 6 …
路程/千米 90 …
①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
②时间和路程成 比例,理由是 .
③利用图象估计一下,2.5时行 千米,行675千米需要 小时.
参考答案与试题解析
一.选择题(共10小题)
1.解:因为=1.2
x=9.6
=1.2
8=1.2y
y=6.
所以x>y.
故选:A.
2.解:A,因为2a=5b,所以=(一定),所以a、b成正比例;
B,因为a×7=,所以=14(一定),所以a、b成正比例;
C,因为a×=1,所以ab=3(一定),所以a、b成反比例;
故选:C.
3.解:=2:1
x:3=2:1
x=6.
故选:A.
4.解::=2:3;
答:张师傅与李师傅的工作效率的比为2:3.
故选:C.
5.解:一个比的前项是30,若前项增加60,可知比的前项由30变成90,相当于前项乘3,
根据比的性质,要使比值不变,后项也应该乘3;
故选:C.
6.解::、
=(×18):(×18)
=3:4(或写成分数比)
故选:BC.
7.解::6=÷6=;
A、2.5:16=2.5÷16=;
B、0.1:=0.1=;
C、3:2.4=3÷2.4=;
D、:4=÷4=;
所以能与:6组成比例的是:4;
故选:D.
8.解:8:15的前项扩大2倍,后项也扩大2倍,
8:15=16:30,
30=15+15,
即8:15的前项扩大2倍,要使它的比值不变,后项应增加15.
故选:B.
9.解:一条直角边为:14÷(3+4)×3,
=14÷7×3,
=6(分米),
另一条直角边为:14﹣6=8(分米),
设斜边上的高为x分米,
6×8÷2=10×x÷2,
10x=48,
x=48÷10,
x=4.8,
答:斜边上的高为4.8分米,
故选:D.
10.解:
(5﹣3)÷5=2÷5=
答:男队人数比女队人数少.
故选:B.
二.填空题(共8小题)
11.解:
3:4=(3×8):(4×8)=24:32
0.8:5=(0.8×3):(5×3)=2.4:15
故答案为:24,2.4.
12.解:1.2:
=(1.2×):(×)
=9:5
1.2:
=1.2÷
=
故答案为:9:5,.
13.解:因为,=Y,则X:Y=5(一定);
所以,XY成正比例;
因为,=Y,则XY=5(一定);
所以,XY成反比例.
故答案为:正,反.
14.解:3.5:x=0.5:20%
0.5x=3.5×20%
0.5x÷0.5=0.7÷0.5
x=1.4;
故答案为:1.4.
15.解:设乙数为x,
则5:3=60:x,
5x=180,
x=36.
故答案为:36.
16.解:甲:乙=3:4=(3×5):(4×5)=15:20;
乙:丙=5:6=(5×4):(6×4)=20:24;
甲:乙:丙=15:20:24;
故答案为:15,20,24.
17.解:2÷10=0.2=20%=8:40=二折.
故答案为:2,20,40,二.
18.解:18÷(5﹣3)
=18÷2
=9(岁);
9×3+9×5
=27+45
=72(岁);
答:甲乙年龄和是72岁.
故答案为:72.
三.判断题(共5小题)
19.解:(1÷12):(1÷15)
=:
=():()
=5:4;
4:5≠5:4,所以原题计算错误;
故答案为:×.
20.解:虽然2:3可以写成,但是仍读作二比三,不能读作三分之二.
因此,2:3可以写成,也可以读成:三分之二是错误的.
故答案为:×.
21.解:比的前项和后项同时乘或除以一个相同的数(0除外),比值不变;
所以原说法错误;
故答案为:×.
22.解:(8﹣7)÷8
=1÷8
=;
所以红花的朵数比黄花少;原题计算正确;
故答案为:√.
23.解:因为每天的平均用煤量×使用的天数=煤的数量(一定),
也就是两种相关联的量的乘积一定,所以,煤的数量一定,使用的天数与每天的平均用煤量成反比例.
原题说法正确.
故答案为:√.
四.计算题(共1小题)
24.解:(1):=:x
x=×
x÷=×÷
x=
(2)0.8:x=3.75:0.75
3.75x=0.8×0.75
3.75x÷3.75=0.8×0.75÷3.75
x=0.16
(3)x:=:4
4x=×
4x÷4=×÷4
x=
(4)(2+x):2=21:6
6(2+x)=21×2
6(2+x)÷6=21×2÷6
2+x=7
2+x﹣2=7﹣2
x=5
(5)=
3.5x=15×28
3.5x÷3.5=15×28÷3.5
x=120
(6)x+×45=12
x+9=12
x+9﹣9=12﹣9
x=3
x÷=3÷
x=12
五.应用题(共6小题)
25.解:(1)====20,是比值一定,所以塑料管的长度和价格成正比例.
(2)===3.75,是比值一定,所以纸的张数和质量成正比例.
(3)=42.5,=22,=17.125,比值不一定,所以强强的年龄和身高不成比例.
(4)===3.14,是比值一定,所以圆的直径和周长成正比例.
26.解:工作量一定,工作时间和工作效率成反比例关系,所以甲乙两人的工作效率比就是6:5;
30÷6×5
=5×5
=25(个)
答:乙每小时加工25个.
27.解:盐都龙:59:50═59÷50=1.18
马:23:25=23÷25=0.92
羚羊:5÷4=5÷4=1.25
1.25>1.18>0.92
答:羚羊跑得最快.
28.解:把木棍的原长设为1,则第四天截取的长度是:
×××=
第四天截取的长度:原来的长度=:1=1:16;
答:笫四天截取的长度与原来木棍总长度的最简单整数比是1:16.
29.解:设原来甲队有7x人,乙队3x人,
(7x﹣30):(3x+30)=3:2
2(7x﹣30)=3(3x﹣30)
14x﹣60=9x﹣90
5x=150
x=30
30×7=210(人)
30×3=90(人)
答:甲筑路队原来有210人,乙筑路队原来有90人.
30.解:①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
时间/时 1 2 3 4 5 6 …
路程/千米 90 180 270 360 450 540 …
②时间和路程成 正比例,理由是 路程÷时间=速度(一定).
③如图
用图象估计一下,2.5时行 225千米,行675千米需要 7.5小时.
故答案为:正,路程÷时间=速度(一定),225,7.5.
