人教版八年级数学上册14.2.1平方差公式课件 (共22张)
文档属性
| 名称 | 人教版八年级数学上册14.2.1平方差公式课件 (共22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-09 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
某校今年暑假将对一部分正方形花圃进行改造,花圃师傅说:“我准备把这些正方形花圃的一边减少5米,相邻的另一边增加5米改成长方形.”你觉得改变前后花圃的面积变了吗?
(a+b)(m+n)
复习旧知 探求新知
=am
+an
+bm
+bn
多项式与多项式是如何相乘的?
问题1.计算下列多项式的积,你能从中发现什么规律吗?
(1)(x+3)(x-3)=
(2)(m+2)(m-2)=
(3)(2x+4)(2x-4)=
x2-3x+3x-9
m2-2m+2m-4
4x2-8x+8x-16
=x2-9
= m2-4
= 4x2-16
自主探索 获取新知
问题2.(3)你能将发现的规律用式子表示出来么?
问题3:你能通过计算(a+b)(a?b),
说明猜想的合理性吗?
问题2:(1)观察、分析相乘的两个多项 式有什么共同特点?
问题2.(2)相乘的两个多项式的各项与它们的积中的各项有什么关系?
平方差公式:
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,等于这两个数的
平方差.
合作探究 得出新知
(a+b)(a-b)
= a2-ab+ba-b2
= a2-b2
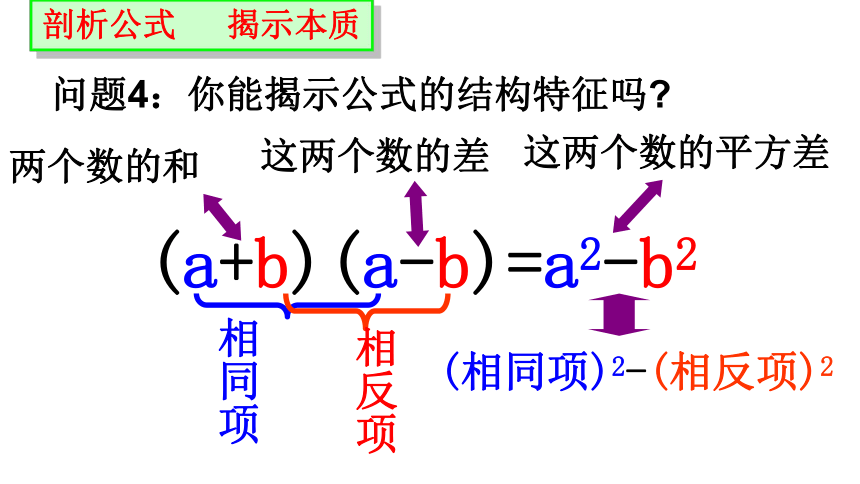
(a+b)(a-b)=a2-b2
两个数的和
这两个数的差
这两个数的平方差
(相同项)2-(相反项)2
相同项
相反项
剖析公式 揭示本质
问题4:你能揭示公式的结构特征吗?
1.下列各式能否用平方差公式进行计算,为什么?
火眼金睛 巩固新知
(a+b)(a-b)=a2-b2
能
能
能
不能
2、口答下列各题:
(l) (y + 3)(y - 3)=_______
(2) (4 + x)(4 - x)= ______
(3) (5 - x)(5 + x)= _______
(4) (p+7 )(p - 7)= _______
(a+b)(a-b)=a2-b2
争先恐后 巩固新知
如果将边长为a的正方形花圃的-边减少b,相邻另-边增加b改为长方形,你能帮他设计出图形吗?
数形结合 几何说理
问题5:现在,你知道花圃师傅说的把花圃形状由正方形改为长方形,面积变了么?
那么花圃的面积变为多少?同原来的面
积相比,发生了怎样的变化?
又因为I 和 II 的面积等于I 和 III 的面积,故
I 和 II 的面积可以表示为:
I 和 III 的面积可以表示为:
(a+b)(a-b)
a2 -b2
(a+b)(a-b)= a2 -b2
数形结合 几何说理
a2-b2
(a+b)(a-b)
(a+b)(a-b)=a2-b2
数形结合 几何说理
阴影部分的面积可以表示为I和II两个梯形的面积,即:
阴影部分的面积还可以表示为大
正方形的面积减小正方形的面积,即:
所以有:(a+b)(a-b)= a2 -b2
数形结合 几何说理
阴影部分的面积可以
表示为长方形面积:
阴影部分的面积还可以表示为大正
方形的面积减小正方形的面积,即:
所以有:(a+b)(a-b)= a2 -b2
即: (a+b)(a-b)
a2 -b2
数形结合 几何说理
例1 :运用平方差公式计算:
(1)(3x+2)(3x-2);
(4)(-x+2y)(-x-2y).
(1)(3x+2)(3x-2);
分析:关键是找出相同的项和相反的项,在这里我们可以把3x看作a,把2看作b,即
(3x+2)(3x- 2)=(3x)2-22
(2) (5+6x)(5-6x)
巩固运用 内化新知
例2、计算:
分析:因为102×98可以写成(100+2)(100-2)的形式,故可以利用平方差进行简化计算。
(1) 102×98
原式= (100+2)(100-2)
=1002-22
=10000-4
=9996
(2) (y+2)(y-2)-(y-1)(y+5)
原式=y2-4-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y+1
拓展深化 发展思维
(1)(b+2a)(2a-b)
(2)(-x+2y)(-x-2y)
请用平方差公式计算下列各题:
锋芒毕露 模拟演练
一、选择:
1.下列各式中,能用平方差公式运算的是( )
A.(-a+b)(-a-b) B.(a-b)(b-a)
C.(2a-3b)(3a+2b) D.(b+c)(-b-c)
2.下列多项式相乘,不能用平方差公式计算的是( )
A.(x-2y)(2y+x) B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y) D.(-2b-5)(2b-5)
A
C
小试牛刀 挑战自我
二、填空:
1、( )( )=n2-m2
2、 ( ) ( ) =( )
3、( )( )=25-a?
n+m
n-m
-2x+3y
-2x-3y
5+a
5-a
4x2-9y2
小试牛刀 挑战自我
三、利用平方差公式计算:
(a-2)(a+2)(a2 + 4)
解:原式=(a2-4)(a2+4)
=a4-16
你能根据上题计算过程得出
(2+1)(22+1)(24+1)(28+1) … (22n+1) 的结果吗?
更上一层楼 知识再探究
(x-6)(x+6)
(-1+x)(-1-x)
(-3x-2y)(2y-3x)
(a-3b) (a-3b)
(5ab+1)(5ab-1)
201×199
(a+b)(a-b)=a2-b2
两个数的和
这两个数的差
这两个数的平方差
(相同项)2-(相反项)2
相同项
相反项
课堂小结 感悟收获
1.必做题
教科书习题14.2 第1题
2.选做题
① (a-b+c)(a-b-c)
② (a-b+c-d)(-a-b-c-d)
布置作业 提高升华
某校今年暑假将对一部分正方形花圃进行改造,花圃师傅说:“我准备把这些正方形花圃的一边减少5米,相邻的另一边增加5米改成长方形.”你觉得改变前后花圃的面积变了吗?
(a+b)(m+n)
复习旧知 探求新知
=am
+an
+bm
+bn
多项式与多项式是如何相乘的?
问题1.计算下列多项式的积,你能从中发现什么规律吗?
(1)(x+3)(x-3)=
(2)(m+2)(m-2)=
(3)(2x+4)(2x-4)=
x2-3x+3x-9
m2-2m+2m-4
4x2-8x+8x-16
=x2-9
= m2-4
= 4x2-16
自主探索 获取新知
问题2.(3)你能将发现的规律用式子表示出来么?
问题3:你能通过计算(a+b)(a?b),
说明猜想的合理性吗?
问题2:(1)观察、分析相乘的两个多项 式有什么共同特点?
问题2.(2)相乘的两个多项式的各项与它们的积中的各项有什么关系?
平方差公式:
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,等于这两个数的
平方差.
合作探究 得出新知
(a+b)(a-b)
= a2-ab+ba-b2
= a2-b2
(a+b)(a-b)=a2-b2
两个数的和
这两个数的差
这两个数的平方差
(相同项)2-(相反项)2
相同项
相反项
剖析公式 揭示本质
问题4:你能揭示公式的结构特征吗?
1.下列各式能否用平方差公式进行计算,为什么?
火眼金睛 巩固新知
(a+b)(a-b)=a2-b2
能
能
能
不能
2、口答下列各题:
(l) (y + 3)(y - 3)=_______
(2) (4 + x)(4 - x)= ______
(3) (5 - x)(5 + x)= _______
(4) (p+7 )(p - 7)= _______
(a+b)(a-b)=a2-b2
争先恐后 巩固新知
如果将边长为a的正方形花圃的-边减少b,相邻另-边增加b改为长方形,你能帮他设计出图形吗?
数形结合 几何说理
问题5:现在,你知道花圃师傅说的把花圃形状由正方形改为长方形,面积变了么?
那么花圃的面积变为多少?同原来的面
积相比,发生了怎样的变化?
又因为I 和 II 的面积等于I 和 III 的面积,故
I 和 II 的面积可以表示为:
I 和 III 的面积可以表示为:
(a+b)(a-b)
a2 -b2
(a+b)(a-b)= a2 -b2
数形结合 几何说理
a2-b2
(a+b)(a-b)
(a+b)(a-b)=a2-b2
数形结合 几何说理
阴影部分的面积可以表示为I和II两个梯形的面积,即:
阴影部分的面积还可以表示为大
正方形的面积减小正方形的面积,即:
所以有:(a+b)(a-b)= a2 -b2
数形结合 几何说理
阴影部分的面积可以
表示为长方形面积:
阴影部分的面积还可以表示为大正
方形的面积减小正方形的面积,即:
所以有:(a+b)(a-b)= a2 -b2
即: (a+b)(a-b)
a2 -b2
数形结合 几何说理
例1 :运用平方差公式计算:
(1)(3x+2)(3x-2);
(4)(-x+2y)(-x-2y).
(1)(3x+2)(3x-2);
分析:关键是找出相同的项和相反的项,在这里我们可以把3x看作a,把2看作b,即
(3x+2)(3x- 2)=(3x)2-22
(2) (5+6x)(5-6x)
巩固运用 内化新知
例2、计算:
分析:因为102×98可以写成(100+2)(100-2)的形式,故可以利用平方差进行简化计算。
(1) 102×98
原式= (100+2)(100-2)
=1002-22
=10000-4
=9996
(2) (y+2)(y-2)-(y-1)(y+5)
原式=y2-4-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y+1
拓展深化 发展思维
(1)(b+2a)(2a-b)
(2)(-x+2y)(-x-2y)
请用平方差公式计算下列各题:
锋芒毕露 模拟演练
一、选择:
1.下列各式中,能用平方差公式运算的是( )
A.(-a+b)(-a-b) B.(a-b)(b-a)
C.(2a-3b)(3a+2b) D.(b+c)(-b-c)
2.下列多项式相乘,不能用平方差公式计算的是( )
A.(x-2y)(2y+x) B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y) D.(-2b-5)(2b-5)
A
C
小试牛刀 挑战自我
二、填空:
1、( )( )=n2-m2
2、 ( ) ( ) =( )
3、( )( )=25-a?
n+m
n-m
-2x+3y
-2x-3y
5+a
5-a
4x2-9y2
小试牛刀 挑战自我
三、利用平方差公式计算:
(a-2)(a+2)(a2 + 4)
解:原式=(a2-4)(a2+4)
=a4-16
你能根据上题计算过程得出
(2+1)(22+1)(24+1)(28+1) … (22n+1) 的结果吗?
更上一层楼 知识再探究
(x-6)(x+6)
(-1+x)(-1-x)
(-3x-2y)(2y-3x)
(a-3b) (a-3b)
(5ab+1)(5ab-1)
201×199
(a+b)(a-b)=a2-b2
两个数的和
这两个数的差
这两个数的平方差
(相同项)2-(相反项)2
相同项
相反项
课堂小结 感悟收获
1.必做题
教科书习题14.2 第1题
2.选做题
① (a-b+c)(a-b-c)
② (a-b+c-d)(-a-b-c-d)
布置作业 提高升华
