人教A版数学必修2第二章 点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质 (课件 共15张PPT)
文档属性
| 名称 | 人教A版数学必修2第二章 点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质 (课件 共15张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 799.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-12 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
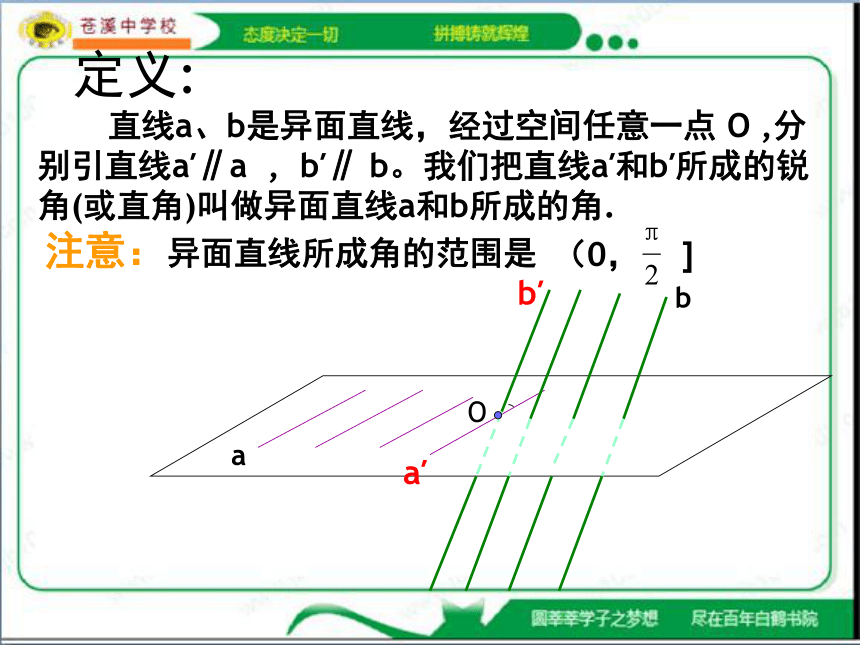
a
b′
b
O
定义:
注意:异面直线所成角的范围是
直线a、b是异面直线,经过空间任意一点 O ,分别引直线a′∥a , b′∥ b。我们把直线a′和b′所成的锐角(或直角)叫做异面直线a和b所成的角.
(0, ]
a′
★求角的步骤:
1. 作……2.证……3.算
求异面直线所成角的步骤有哪些?
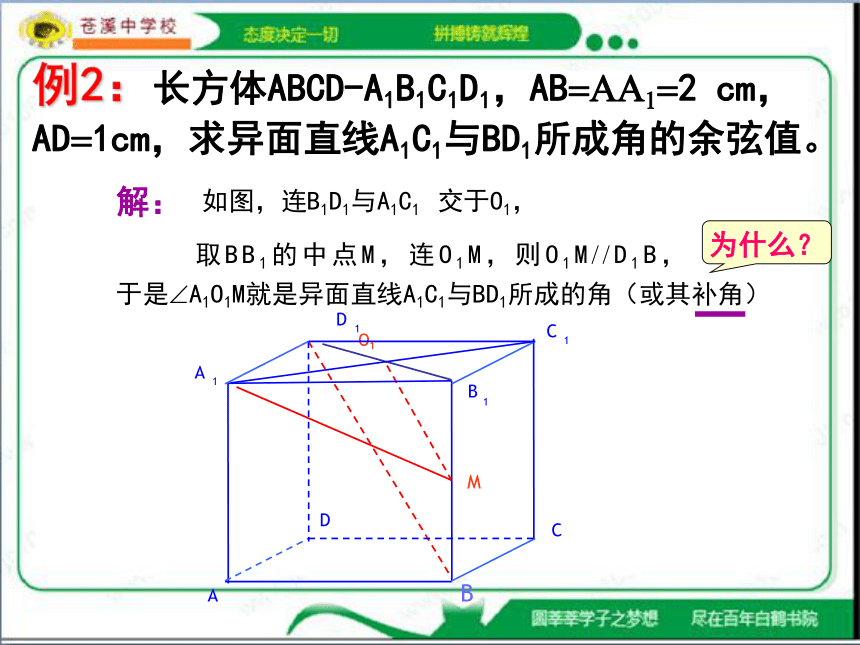
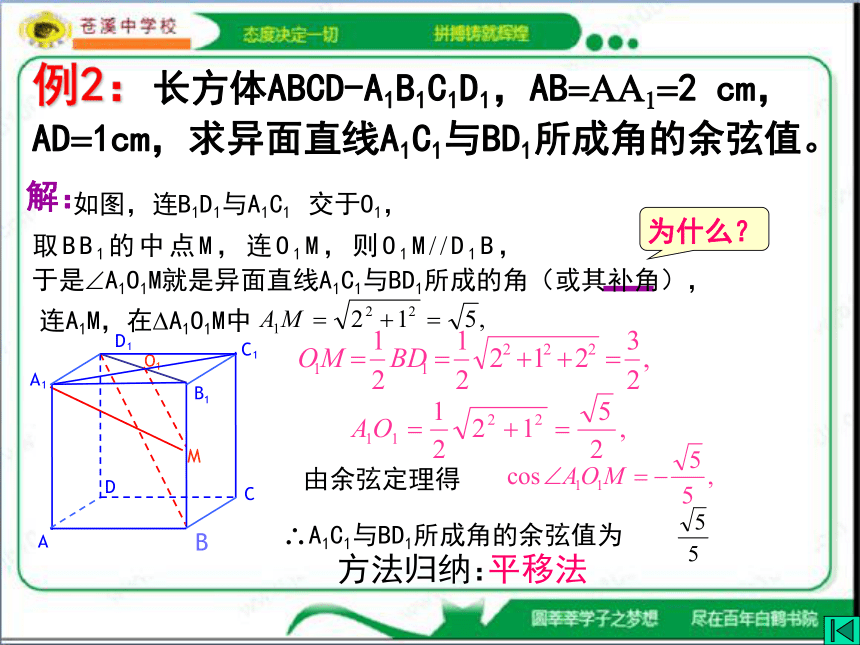
例2:长方体ABCD-A1B1C1D1,AB=AA1=2 cm, AD=1cm,求异面直线A1C1与BD1所成角的余弦值。
取BB1的中点M,连O1M,则O1M??D1B,
如图,连B1D1与A1C1 交于O1,
于是?A1O1M就是异面直线A1C1与BD1所成的角(或其补角)
O1
M
解:
为什么?
由余弦定理得
?A1C1与BD1所成角的余弦值为
方法归纳:
平移法
连A1M,在?A1O1M中
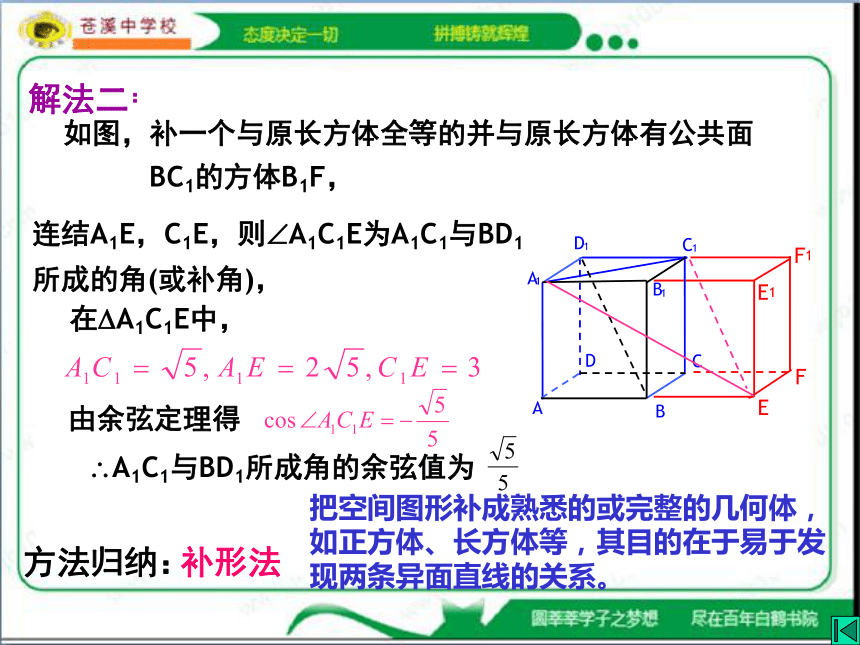
解法二:
方法归纳:
补形法
把空间图形补成熟悉的或完整的几何体,如正方体、长方体等,其目的在于易于发现两条异面直线的关系。
在?A1C1E中,
由余弦定理得
?A1C1与BD1所成角的余弦值为
如图,补一个与原长方体全等的并与原长方体有公共面
连结A1E,C1E,则?A1C1E为A1C1与BD1所成的角(或补角),
BC1的方体B1F,
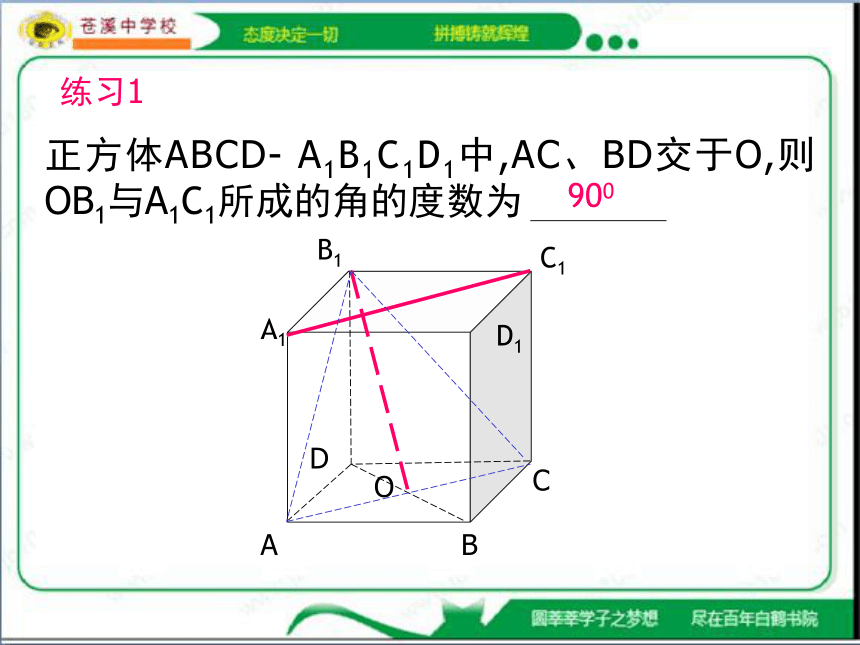
正方体ABCD- A1B1C1D1中,AC、BD交于O,则OB1与A1C1所成的角的度数为
练习1
900
在正四面体S-ABC中,SA⊥BC, E, F分别为SC、AB 的中点,那么异面直线EF 与SA 所成的角等于( )
C
D
(A)300 (B)450 (C)600 (D)900
练习2
B
G
练习2(解法二)
练习2
(解法三)
在正方体AC1中,M,N分别是A1A和B1B的中点,求异面直线CM和D1N所成的角?
M
N
三、解答题
已知正方体的棱长为 a , M 为 AB 的中点, N 为 BB1的中点,求 A1M 与 C1 N 所成角的余弦值。
解:
E
G
如图,取AB的中点E, 连BE, 有BE∥ A1M
取CC1的中点G,连BG. 有BG∥ C1N
则∠EBG即为所求角。
BG=BE= a, F C1 = a
由余弦定理,
cos∠EBG=2/5
F
取EB1的中点F,连NF,有BE∥NF
则∠FNC为所求角。
想一想:
还有其它定角的方法吗?
在△EBG中
空间四边形P-ABC中,M,N分别是PB,AC的中点,PA=BC=6,MN=4,求PA与BC所成的角的余弦值。
E
如图,正三棱锥S-A BC的侧棱与底面边长相等,如果E、F分别为SC、 A B的中点,那么异面直线EF与SA所成角等于( ) A.90° B.60° C.45° D.30°
返回
定角一般方法有:
(1)平移法(常用方法)
小结:
1、求异面直线所成的角是把空间角转化为平面 角,体现了化归的数学思想。
2、用余弦定理求异面直线所成角时,要注意角的 范围:
(1) 当 cosθ > 0 时,所成角为 θ
(2) 当 cosθ < 0 时,所成角为π- θ
(3) 当 cosθ = 0 时,所成角为
3、当异面直线垂直时,还可应用线面垂直的有 关知识解决。
90o
(2)补形法
化归的一般步骤是:
定角
求角
a
b′
b
O
定义:
注意:异面直线所成角的范围是
直线a、b是异面直线,经过空间任意一点 O ,分别引直线a′∥a , b′∥ b。我们把直线a′和b′所成的锐角(或直角)叫做异面直线a和b所成的角.
(0, ]
a′
★求角的步骤:
1. 作……2.证……3.算
求异面直线所成角的步骤有哪些?
例2:长方体ABCD-A1B1C1D1,AB=AA1=2 cm, AD=1cm,求异面直线A1C1与BD1所成角的余弦值。
取BB1的中点M,连O1M,则O1M??D1B,
如图,连B1D1与A1C1 交于O1,
于是?A1O1M就是异面直线A1C1与BD1所成的角(或其补角)
O1
M
解:
为什么?
由余弦定理得
?A1C1与BD1所成角的余弦值为
方法归纳:
平移法
连A1M,在?A1O1M中
解法二:
方法归纳:
补形法
把空间图形补成熟悉的或完整的几何体,如正方体、长方体等,其目的在于易于发现两条异面直线的关系。
在?A1C1E中,
由余弦定理得
?A1C1与BD1所成角的余弦值为
如图,补一个与原长方体全等的并与原长方体有公共面
连结A1E,C1E,则?A1C1E为A1C1与BD1所成的角(或补角),
BC1的方体B1F,
正方体ABCD- A1B1C1D1中,AC、BD交于O,则OB1与A1C1所成的角的度数为
练习1
900
在正四面体S-ABC中,SA⊥BC, E, F分别为SC、AB 的中点,那么异面直线EF 与SA 所成的角等于( )
C
D
(A)300 (B)450 (C)600 (D)900
练习2
B
G
练习2(解法二)
练习2
(解法三)
在正方体AC1中,M,N分别是A1A和B1B的中点,求异面直线CM和D1N所成的角?
M
N
三、解答题
已知正方体的棱长为 a , M 为 AB 的中点, N 为 BB1的中点,求 A1M 与 C1 N 所成角的余弦值。
解:
E
G
如图,取AB的中点E, 连BE, 有BE∥ A1M
取CC1的中点G,连BG. 有BG∥ C1N
则∠EBG即为所求角。
BG=BE= a, F C1 = a
由余弦定理,
cos∠EBG=2/5
F
取EB1的中点F,连NF,有BE∥NF
则∠FNC为所求角。
想一想:
还有其它定角的方法吗?
在△EBG中
空间四边形P-ABC中,M,N分别是PB,AC的中点,PA=BC=6,MN=4,求PA与BC所成的角的余弦值。
E
如图,正三棱锥S-A BC的侧棱与底面边长相等,如果E、F分别为SC、 A B的中点,那么异面直线EF与SA所成角等于( ) A.90° B.60° C.45° D.30°
返回
定角一般方法有:
(1)平移法(常用方法)
小结:
1、求异面直线所成的角是把空间角转化为平面 角,体现了化归的数学思想。
2、用余弦定理求异面直线所成角时,要注意角的 范围:
(1) 当 cosθ > 0 时,所成角为 θ
(2) 当 cosθ < 0 时,所成角为π- θ
(3) 当 cosθ = 0 时,所成角为
3、当异面直线垂直时,还可应用线面垂直的有 关知识解决。
90o
(2)补形法
化归的一般步骤是:
定角
求角
