第二章 第三节 匀变速直线运动的位移与时间的关系 (共49张PPT)
文档属性
| 名称 | 第二章 第三节 匀变速直线运动的位移与时间的关系 (共49张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 874.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-12-10 00:00:00 | ||
图片预览








文档简介
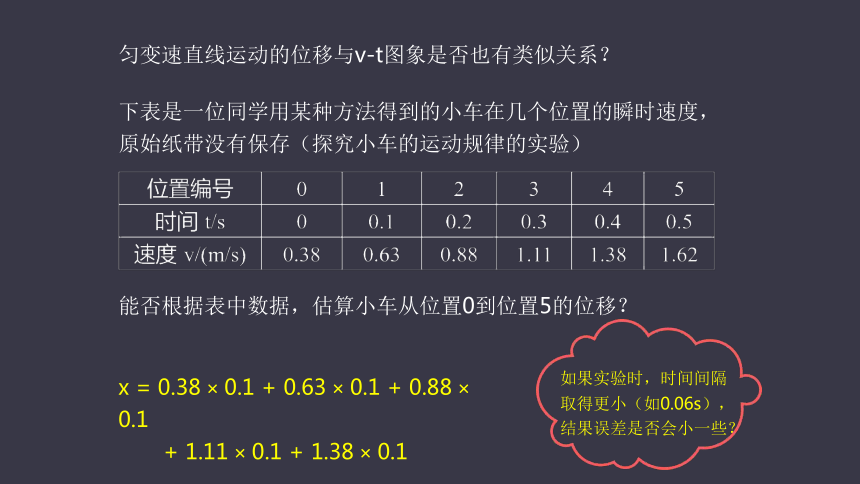
课件49张PPT。匀变速直线运动的位移与时间的关系匀速直线运动的位移公式?在时间 t 内的位移:x = vt在 v-t 图象中如何表示匀速直线运动的位移?对于匀速直线运动,物体的位移对应着 v-t 图象中一块矩形的面积匀变速直线运动的位移与v-t图象是否也有类似关系?下表是一位同学用某种方法得到的小车在几个位置的瞬时速度,原始纸带没有保存(探究小车的运动规律的实验)能否根据表中数据,估算小车从位置0到位置5的位移?x = 0.38 × 0.1 + 0.63 × 0.1 + 0.88 × 0.1?
? ? ? ?+ 1.11 × 0.1 + 1.38 × 0.1如果实验时,时间间隔取得更小(如0.06s),结果误差是否会小一些?以上过程中体现了什么科学思想?无限分割,逐渐逼近,再累加——微元法
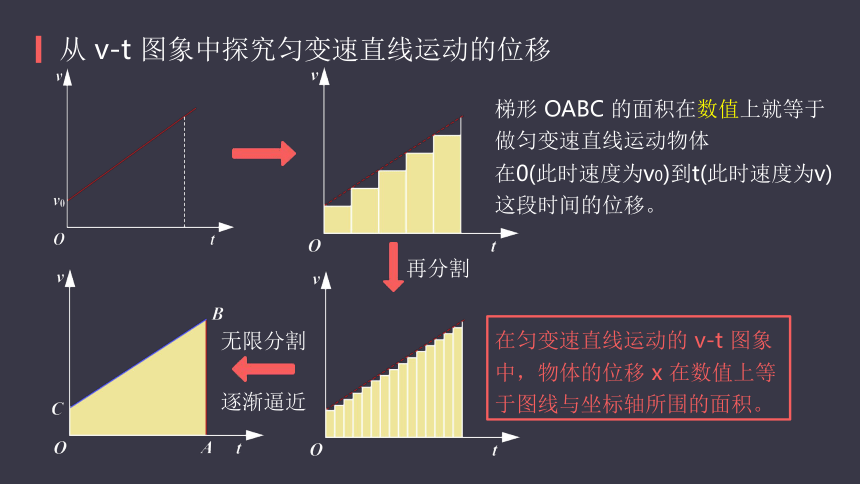
此科学思想方法能否应用到 v-t 图象上?从 v-t 图象中探究匀变速直线运动的位移梯形 OABC 的面积在数值上就等于做匀变速直线运动物体
在0(此时速度为v0)到t(此时速度为v)
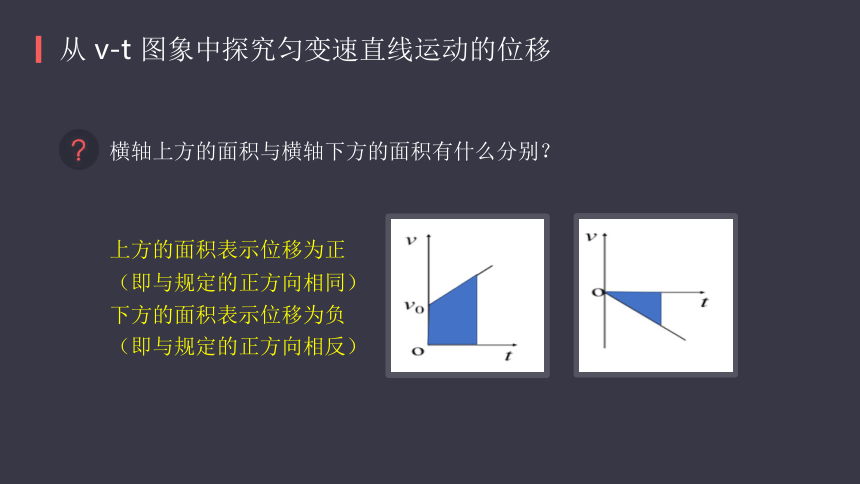
这段时间的位移。在匀变速直线运动的 v-t 图象中,物体的位移 x 在数值上等于图线与坐标轴所围的面积。逐渐逼近再分割无限分割横轴上方的面积与横轴下方的面积有什么分别?从 v-t 图象中探究匀变速直线运动的位移上方的面积表示位移为正
(即与规定的正方向相同)
下方的面积表示位移为负
(即与规定的正方向相反)从 v-t 图象中探究匀变速直线运动的位移一质点以一定初速度沿竖直方向抛出,得到它的 v-t 图象如图所示,试求出它在前 2s 内的位移;前 4s 内的位移。前 2s 内物体的位移为 5m
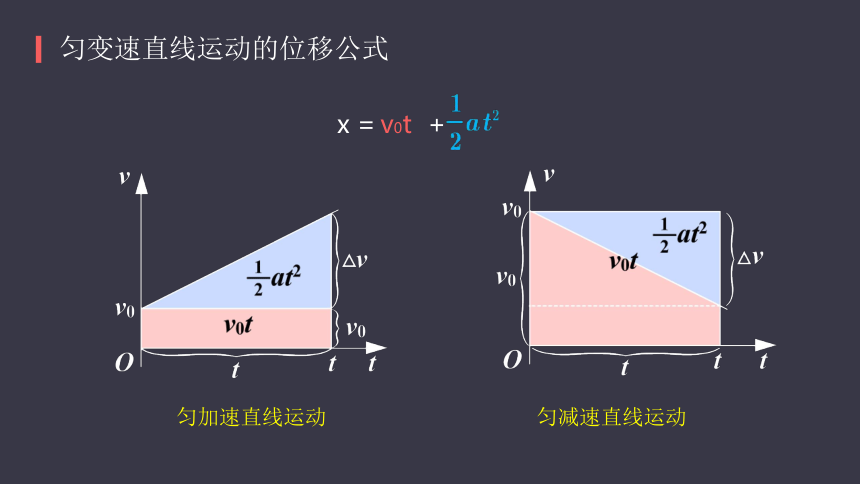
前 4s 内物体的位移为 0注意:当图象在时间轴下方时,表示的位移为负。?试根据下面的 v-t 图计算 0-10s 内物体的位移?x = 5 × 10 ? 5π?从 v-t 图象中探究匀变速直线运动的位移的拓展匀变速直线运动的位移公式能否利用上述结论找出匀变速直线运动的位移与时间的关系式呢?匀变速直线运动位移与时间的关系式(简称位移公式)S =(OC +AB ) × OA / 2v = v0?+ at匀变速直线运动的位移公式若位移的计算结果为正值 说明这段时间内位移的方向与规定的正方向相同 若位移的计算结果为负值 说明这段时间内位移的方向与规定的正方向相反 若物体做匀加速直线运动a与v0同向,a取正值 若物体做匀减速直线运动a与v0反向,a取负值 x =? ? ? ?+v0t匀变速直线运动的位移公式匀加速直线运动匀减速直线运动匀变速直线运动的位移公式①公式中的 x 、v0、a 均为矢量,应用时必须选取统一方向为正方向。一般规定初速度的方向为正方向②利用此式和 v = v0+ at 综合应用,可以解决所有的匀变速直线运动问题。注意:位移时间公式的应用一辆汽车以 1m/s2 的加速度加速行驶了 12s,驶过了 180m 。汽车开始加速时的速度是多少?已知汽车刹车后 10s 停下来,且汽车在匀减速直线运动时的加速度大小为 1m/s2。位移时间公式的应用(1)求汽车从刹车直到停止时的位移。(2)求汽车停止前最后 1s 内的位移。50m0.5m末速度为零的匀减速直线运动可看成初速度为零,加速度大小相等的匀加速直线运动的逆过程。位移时间公式的应用在平直公路上,一汽车的速度为 15m/s,从某时刻开始刹车,在阻力作用下,汽车以 2m/s2 的加速度运动,问刹车后 10s 末车离开始刹车点多远?车做减速运动,是否运动了10s?初速度v0=15m/s,a=-2m/s2,分析得知车运动 7.5s 就会停下,在后 2.5s 内,车停止不动解 设车实际运动时间为t,vt=0, a=-2m/s2?由v = v0?+ at 知:运动时间:所以车的位移为:一个物体做匀减速直线运动,v0=60m/s,a=10m/s2,求物体运动 100m 所需要的时间t。位移时间公式的应用t=2s 或 10s位移时间公式的应用一辆汽车以 2m/s2 的加速度从静止开始加速运动,求该车在第 5 秒内的平均速度。第 5 秒内的位移 Δs 可以用前 5 秒的位移减去前 4 秒的位移得到 不是5秒,而是1秒解:以汽车前进方向为正方向,那么汽车的加速度为正,初速度为 0位移时间公式的应用一辆汽车以 2m/s2 的加速度从静止开始加速运动,求该车在第 5 秒内的平均速度。某同学的方法:
利用公式vt=v0+at第 5 秒初(第 4 秒末)的速度第 5 秒末的速度则第 5 秒内的平均速度平均速度就是初末速度的平均吗?位移时间公式的应用求下面做直线运动的物体在 0-4s 内的平均速度。0-1s 内,物体的速度从0均匀变化到 v=2m/s1-4s 内,物体的速度一直保持 v=2m/s则 0-4s 内物体的总位移求下面做直线运动的物体在 0-4s 内的平均速度。位移时间公式的应用研究 0-4 秒内初末速度的平均值:0-4 秒内位移的图象解法:0-4 秒内物体的总位移即为 v-t 图象与 t 轴所围的面积:位移时间公式的应用一物体作直线运动的速度图象如图所示,则下列说法错误的是(? ? ? )?? A.前 2s 内做匀加速直线运动
B.前 4s 内做匀变速直线运动
C.前 4s 内的平均速度为 2m/s
D.后 2s 内的加速度为 -1.5m/s2?B位移时间公式的应用以 36km/h 速度行驶的列车开始下坡,在坡路上的加速度等于 0.2m/s2,经过 30s到达坡底,求坡路的长度和列车到达坡底时的速度位移时间公式的应用以 18m/s 的速度行驶的汽车,制动后做匀减速运动,在 3s 内前进 36m,求汽车的加速度位移——时间图象在平面直角坐标系中,用横轴表示时间 t,用纵轴表示位移 x,根据物体运动情况做出的位移随时间变化的图象叫做位移——时间图象,简称位移图象表示汽车做匀速直线运动匀速直线运动的 x-t 图象是一条直线某汽车的 x-t 图象位移——时间图象匀变速直线运动的 x-t 图象是怎样的?(讨论匀加速直线运动)匀变速直线运动的 x-t 图象是一条抛物线位移——时间图象运用初中数学课中学过的函数图像知识,你能画出初速度为 0 的匀变速直线运动 x = at2 / 2 的 x-t 图像的草图吗?匀变速直线运动在 x-t 图象中是一条抛物线注意:x-t 图象不是物体运动的轨迹位移——时间图象从给定的 x-t 图象中,我们可以得到什么信息?①质点在任意一段时间内的位移
②发生一段位移所需要的时间
③斜率表示物体运动的速度注意:
x-t 图象表示的是位移随时间变化的情况,绝不是运动的径迹一辆汽车在教练场上沿着平直道路行驶,以 x 表示它对于出发点的位移。如图所示,为汽车在t=0 到 t=40s 这段时间的 x-t 图象。通过分析回答以下问题
(1)汽车最远距离出发点多少米?
(2)汽车在哪段时间没有行驶?
(3)汽车在哪段时间驶离出发点,在哪段时间驶向出发点?位移——时间图象30m10~20s0-10s 内驶离出发点,20~40s 内驶向出发点位移——时间图象A,A’两个物体在做匀速直线运动,速度分别为v、v’(v’>v),从计时开始到时刻t 的位移分别为 x,x’
(1)写出两个物体的位移与时间的关系式
(2)在同一个坐标系中分别作出两个物体的速度——时间图象的草图
(3)在同一个坐标系中分别作出两个物体的位移——时间图象的草图x = vt ,? ? ? x' = v'tv < v'匀变速直线运动平均速度、首尾速度、中点时刻速度的关系?中点时刻速度和平均速度中点时刻速度和平均速度匀变速直线运动平均速度、首尾速度、中点时刻速度的关系注意:此公式仅对匀变速直线运动成立,非匀变速运动不能使用。一质点做匀变速直线运动,初速度 v0=2m/s,4s 内位移为 20m,求:
(1)质点 4s 末的速度
(2)质点 2s 末的速度中点时刻速度和平均速度解法一 : 利用平均速度公式?4s 内的平均速度代入数据解得,4s 末的速度2s 末的速度(1)8m/s(2)5m/s解法二 :?利用两个基本公式质点 4s 末的速度2s 末的速度由得再由得中点时刻速度和平均速度两木块自左向右运动,现用高速摄影机在同一底片上多次曝光,记录下木块每次曝光时的位置,如图所示,连续两次曝光的时间间隔是相等的,由图可知(? ? ? ? ? )A . 在时刻 t2?以及时刻 t5?两木块速度相同
B . 在时刻 t1?两木块速度相同
C . 在时刻 t3?和时刻 t4?之间某瞬间两木块速度相同
D . 在时刻 t4?和时刻 t5?之间某瞬时两木块速度相同C匀变速直线运动连续相等时间位移特点?一质点做匀变速直线运动,在相同时间内的位移分别为x1、x2、 x3…那么这些位移具有什么样的特点呢?v0v1v2v3相邻相等时间的位移差是个定值等差数列匀变速直线运动连续相等时间位移特点?阴影面积即相邻相等时间的位移差一质点做匀变速直线运动,在相同时间内的位移分别为x1、x2、 x3…那么这些位移具有什么样的特点呢?Δx=t×at =at2?匀变速直线运动连续相等时间位移特点?①判断物体是否做匀变速直线运动如果? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?成立,则a为一恒量,说明物体做匀变速直线运动②求加速度 利用? ? ? ? ? ? ? ? ?,可求得?应用:匀变速直线运动连续相等时间位移特点?做匀加速直线运动的物体,从开始计时起连续两个 4s 的时间间隔内通过的位移分别是 48m 和 80m,则这个物体的初速度和加速度各是多少?8m/s,2m/s2?解法一根据关系式物体的加速度a=由于前 4s 内的位移故初速度解法二设物体的初速度和加速度分别为v0,a由公式前 4s 内的位移前 8s 内的位移解以上两式得匀变速直线运动连续相等时间位移特点?一个做匀变速直线运动的物体,初速度为 0.5m/s,在第 9s 内的位移比第 5s 内的位移多 4m,求:
(1)物体的加速度
(2)物体在 9s 内通过的位移(1)1m/s2(2)45m匀变速直线运动连续相等时间位移特点?一小球沿斜面匀加速滑下,依次经过A、B、C 三点。已知AB=6m,BC =10m,小球经过AB 和BC 两段所用的时间均为 2s,则小球经过A、B、C 三点时的速度大小分别是(? ? ? ? ? )A.2m/s,3m/s,4m/s
B. 2m/s,4m/s,6m/s
C. 3m/s,4m/s,5m/s
D. 3m/s,5m/s,7m/sB匀变速直线运动连续相等时间位移特点?(多选)一质点做匀加速直线运动,它在第 3s 内的位移是2.0m,第 4s 内的位移是 2.5m,那么可以知道(? ? ? ? ?)?A.质点的加速度是0.5m/s2
B.质点在这两秒内的平均速度是2.25m/s
C.质点在第3s末的瞬时速度是2.25m/s
D.质点在第4s末的瞬时速度是2.5m/sABC初速度为零的匀变速直线运动的位移特点一质点做初速度为0的匀加速直线运动。若初速度为0,则该式简化为:ts 末、2t 末、 3t 末‥ ‥ ‥nt 末的速度之比为多少?由v = at 知,V ∝ t
故ts 末、2t 末、 3t 末‥ ‥ nt 末的 速度之比为:1:2:3: ‥ ‥ n t 内、2t 内、 3t 内‥ ‥ ‥nt 内的位移之比为多少?由? ? ? ? ? ? ? ? 知 , x ∝ t2? 故t 内、2t 内、 3t 内‥ ‥nt 内
的位移之比为:1 : 22??: 32??: …… : n2??其速度时间关系式:初速度为零的匀变速直线运动v = at初速度为零的匀变速直线运动的位移特点初速度为零的匀变速直线运动的位移时间关系式:速度时间关系式:v = at一质点做初速度为0的匀加速直线运动。第 1 个 ts 内、第 2 个 t 内、 第 3 个 t 内‥‥ 第 n 个 t 内的位移之比为多少?第 1 个 ts 内位移为第 2 个 t 内位移为第 3 个 ts 内的位移为第 nt 内位移为第 1 个ts 内、第 2 个 t 内、 第 3 个 t 内‥‥ 第 n 个 t 内的位移之比为1:3:5:‥‥(2n-1)初速度为零的匀变速直线运动的位移特点对于末速度为零的匀减速直线运动,上述结论是否可以使用?对于末速度为零的匀减速直线运动,可把它看成逆向的初速度为零的匀加速直线运动,应用比例关系,可使问题简化初速度为零的匀变速直线运动的位移特点如图所示,一小球从 A 点由静止开始沿斜面做匀变速直线运动,若到达 B 点时速度为 v,到达 C 点时速度为 2v,则 AB:AC 等于(? ? ? ? )A . 1:1
B . 1:2
C . 1:3
D . 1:4D初速度为零的匀变速直线运动的位移特点速度、加速度的测量通常比位移的测量要复杂些,而有的时候我们只需比较两个物体运动的加速度,并不需要知道加速度的大小,例如比较两辆汽车的加速性能就是这样。如果已知两个物体在相同时间内从静止开始运动的位移之比,怎样根据运动学的规律由此求出它们的加速度之比?初速度为零的匀变速直线运动的时间特点从运动起点划分为连续相等位移 x,则:位移 x、2x、3x……nx 内的时间之比为?第 1 段位移 x、第 2 段位移 x、第 3 段位移 x 内的时间之比为?v = at初速度为零的匀变速直线运动的时间特点一列火车由静止以恒定的加速度启动出站,设每列车厢的长度相同,不计车厢间隙距离,一观察者站在第一列车厢最前面,他通过测时间估算出第一列车厢尾驶过他时的速度为 v0,则第 n 列车厢尾驶过他时的速度为(? ? ? ? ? )C匀变速直线运动规律:总结速度公式:位移公式:平均速度:v=v0+at
下方的面积表示位移为负
(即与规定的正方向相反)从 v-t 图象中探究匀变速直线运动的位移一质点以一定初速度沿竖直方向抛出,得到它的 v-t 图象如图所示,试求出它在前 2s 内的位移;前 4s 内的位移。前 2s 内物体的位移为 5m
前 4s 内物体的位移为 0注意:当图象在时间轴下方时,表示的位移为负。?试根据下面的 v-t 图计算 0-10s 内物体的位移?x = 5 × 10 ? 5π?从 v-t 图象中探究匀变速直线运动的位移的拓展匀变速直线运动的位移公式能否利用上述结论找出匀变速直线运动的位移与时间的关系式呢?匀变速直线运动位移与时间的关系式(简称位移公式)S =(OC +AB ) × OA / 2v = v0?+ at匀变速直线运动的位移公式若位移的计算结果为正值 说明这段时间内位移的方向与规定的正方向相同 若位移的计算结果为负值 说明这段时间内位移的方向与规定的正方向相反 若物体做匀加速直线运动a与v0同向,a取正值 若物体做匀减速直线运动a与v0反向,a取负值 x =? ? ? ?+v0t匀变速直线运动的位移公式匀加速直线运动匀减速直线运动匀变速直线运动的位移公式①公式中的 x 、v0、a 均为矢量,应用时必须选取统一方向为正方向。一般规定初速度的方向为正方向②利用此式和 v = v0+ at 综合应用,可以解决所有的匀变速直线运动问题。注意:位移时间公式的应用一辆汽车以 1m/s2 的加速度加速行驶了 12s,驶过了 180m 。汽车开始加速时的速度是多少?已知汽车刹车后 10s 停下来,且汽车在匀减速直线运动时的加速度大小为 1m/s2。位移时间公式的应用(1)求汽车从刹车直到停止时的位移。(2)求汽车停止前最后 1s 内的位移。50m0.5m末速度为零的匀减速直线运动可看成初速度为零,加速度大小相等的匀加速直线运动的逆过程。位移时间公式的应用在平直公路上,一汽车的速度为 15m/s,从某时刻开始刹车,在阻力作用下,汽车以 2m/s2 的加速度运动,问刹车后 10s 末车离开始刹车点多远?车做减速运动,是否运动了10s?初速度v0=15m/s,a=-2m/s2,分析得知车运动 7.5s 就会停下,在后 2.5s 内,车停止不动解 设车实际运动时间为t,vt=0, a=-2m/s2?由v = v0?+ at 知:运动时间:所以车的位移为:一个物体做匀减速直线运动,v0=60m/s,a=10m/s2,求物体运动 100m 所需要的时间t。位移时间公式的应用t=2s 或 10s位移时间公式的应用一辆汽车以 2m/s2 的加速度从静止开始加速运动,求该车在第 5 秒内的平均速度。第 5 秒内的位移 Δs 可以用前 5 秒的位移减去前 4 秒的位移得到 不是5秒,而是1秒解:以汽车前进方向为正方向,那么汽车的加速度为正,初速度为 0位移时间公式的应用一辆汽车以 2m/s2 的加速度从静止开始加速运动,求该车在第 5 秒内的平均速度。某同学的方法:
利用公式vt=v0+at第 5 秒初(第 4 秒末)的速度第 5 秒末的速度则第 5 秒内的平均速度平均速度就是初末速度的平均吗?位移时间公式的应用求下面做直线运动的物体在 0-4s 内的平均速度。0-1s 内,物体的速度从0均匀变化到 v=2m/s1-4s 内,物体的速度一直保持 v=2m/s则 0-4s 内物体的总位移求下面做直线运动的物体在 0-4s 内的平均速度。位移时间公式的应用研究 0-4 秒内初末速度的平均值:0-4 秒内位移的图象解法:0-4 秒内物体的总位移即为 v-t 图象与 t 轴所围的面积:位移时间公式的应用一物体作直线运动的速度图象如图所示,则下列说法错误的是(? ? ? )?? A.前 2s 内做匀加速直线运动
B.前 4s 内做匀变速直线运动
C.前 4s 内的平均速度为 2m/s
D.后 2s 内的加速度为 -1.5m/s2?B位移时间公式的应用以 36km/h 速度行驶的列车开始下坡,在坡路上的加速度等于 0.2m/s2,经过 30s到达坡底,求坡路的长度和列车到达坡底时的速度位移时间公式的应用以 18m/s 的速度行驶的汽车,制动后做匀减速运动,在 3s 内前进 36m,求汽车的加速度位移——时间图象在平面直角坐标系中,用横轴表示时间 t,用纵轴表示位移 x,根据物体运动情况做出的位移随时间变化的图象叫做位移——时间图象,简称位移图象表示汽车做匀速直线运动匀速直线运动的 x-t 图象是一条直线某汽车的 x-t 图象位移——时间图象匀变速直线运动的 x-t 图象是怎样的?(讨论匀加速直线运动)匀变速直线运动的 x-t 图象是一条抛物线位移——时间图象运用初中数学课中学过的函数图像知识,你能画出初速度为 0 的匀变速直线运动 x = at2 / 2 的 x-t 图像的草图吗?匀变速直线运动在 x-t 图象中是一条抛物线注意:x-t 图象不是物体运动的轨迹位移——时间图象从给定的 x-t 图象中,我们可以得到什么信息?①质点在任意一段时间内的位移
②发生一段位移所需要的时间
③斜率表示物体运动的速度注意:
x-t 图象表示的是位移随时间变化的情况,绝不是运动的径迹一辆汽车在教练场上沿着平直道路行驶,以 x 表示它对于出发点的位移。如图所示,为汽车在t=0 到 t=40s 这段时间的 x-t 图象。通过分析回答以下问题
(1)汽车最远距离出发点多少米?
(2)汽车在哪段时间没有行驶?
(3)汽车在哪段时间驶离出发点,在哪段时间驶向出发点?位移——时间图象30m10~20s0-10s 内驶离出发点,20~40s 内驶向出发点位移——时间图象A,A’两个物体在做匀速直线运动,速度分别为v、v’(v’>v),从计时开始到时刻t 的位移分别为 x,x’
(1)写出两个物体的位移与时间的关系式
(2)在同一个坐标系中分别作出两个物体的速度——时间图象的草图
(3)在同一个坐标系中分别作出两个物体的位移——时间图象的草图x = vt ,? ? ? x' = v'tv < v'匀变速直线运动平均速度、首尾速度、中点时刻速度的关系?中点时刻速度和平均速度中点时刻速度和平均速度匀变速直线运动平均速度、首尾速度、中点时刻速度的关系注意:此公式仅对匀变速直线运动成立,非匀变速运动不能使用。一质点做匀变速直线运动,初速度 v0=2m/s,4s 内位移为 20m,求:
(1)质点 4s 末的速度
(2)质点 2s 末的速度中点时刻速度和平均速度解法一 : 利用平均速度公式?4s 内的平均速度代入数据解得,4s 末的速度2s 末的速度(1)8m/s(2)5m/s解法二 :?利用两个基本公式质点 4s 末的速度2s 末的速度由得再由得中点时刻速度和平均速度两木块自左向右运动,现用高速摄影机在同一底片上多次曝光,记录下木块每次曝光时的位置,如图所示,连续两次曝光的时间间隔是相等的,由图可知(? ? ? ? ? )A . 在时刻 t2?以及时刻 t5?两木块速度相同
B . 在时刻 t1?两木块速度相同
C . 在时刻 t3?和时刻 t4?之间某瞬间两木块速度相同
D . 在时刻 t4?和时刻 t5?之间某瞬时两木块速度相同C匀变速直线运动连续相等时间位移特点?一质点做匀变速直线运动,在相同时间内的位移分别为x1、x2、 x3…那么这些位移具有什么样的特点呢?v0v1v2v3相邻相等时间的位移差是个定值等差数列匀变速直线运动连续相等时间位移特点?阴影面积即相邻相等时间的位移差一质点做匀变速直线运动,在相同时间内的位移分别为x1、x2、 x3…那么这些位移具有什么样的特点呢?Δx=t×at =at2?匀变速直线运动连续相等时间位移特点?①判断物体是否做匀变速直线运动如果? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?成立,则a为一恒量,说明物体做匀变速直线运动②求加速度 利用? ? ? ? ? ? ? ? ?,可求得?应用:匀变速直线运动连续相等时间位移特点?做匀加速直线运动的物体,从开始计时起连续两个 4s 的时间间隔内通过的位移分别是 48m 和 80m,则这个物体的初速度和加速度各是多少?8m/s,2m/s2?解法一根据关系式物体的加速度a=由于前 4s 内的位移故初速度解法二设物体的初速度和加速度分别为v0,a由公式前 4s 内的位移前 8s 内的位移解以上两式得匀变速直线运动连续相等时间位移特点?一个做匀变速直线运动的物体,初速度为 0.5m/s,在第 9s 内的位移比第 5s 内的位移多 4m,求:
(1)物体的加速度
(2)物体在 9s 内通过的位移(1)1m/s2(2)45m匀变速直线运动连续相等时间位移特点?一小球沿斜面匀加速滑下,依次经过A、B、C 三点。已知AB=6m,BC =10m,小球经过AB 和BC 两段所用的时间均为 2s,则小球经过A、B、C 三点时的速度大小分别是(? ? ? ? ? )A.2m/s,3m/s,4m/s
B. 2m/s,4m/s,6m/s
C. 3m/s,4m/s,5m/s
D. 3m/s,5m/s,7m/sB匀变速直线运动连续相等时间位移特点?(多选)一质点做匀加速直线运动,它在第 3s 内的位移是2.0m,第 4s 内的位移是 2.5m,那么可以知道(? ? ? ? ?)?A.质点的加速度是0.5m/s2
B.质点在这两秒内的平均速度是2.25m/s
C.质点在第3s末的瞬时速度是2.25m/s
D.质点在第4s末的瞬时速度是2.5m/sABC初速度为零的匀变速直线运动的位移特点一质点做初速度为0的匀加速直线运动。若初速度为0,则该式简化为:ts 末、2t 末、 3t 末‥ ‥ ‥nt 末的速度之比为多少?由v = at 知,V ∝ t
故ts 末、2t 末、 3t 末‥ ‥ nt 末的 速度之比为:1:2:3: ‥ ‥ n t 内、2t 内、 3t 内‥ ‥ ‥nt 内的位移之比为多少?由? ? ? ? ? ? ? ? 知 , x ∝ t2? 故t 内、2t 内、 3t 内‥ ‥nt 内
的位移之比为:1 : 22??: 32??: …… : n2??其速度时间关系式:初速度为零的匀变速直线运动v = at初速度为零的匀变速直线运动的位移特点初速度为零的匀变速直线运动的位移时间关系式:速度时间关系式:v = at一质点做初速度为0的匀加速直线运动。第 1 个 ts 内、第 2 个 t 内、 第 3 个 t 内‥‥ 第 n 个 t 内的位移之比为多少?第 1 个 ts 内位移为第 2 个 t 内位移为第 3 个 ts 内的位移为第 nt 内位移为第 1 个ts 内、第 2 个 t 内、 第 3 个 t 内‥‥ 第 n 个 t 内的位移之比为1:3:5:‥‥(2n-1)初速度为零的匀变速直线运动的位移特点对于末速度为零的匀减速直线运动,上述结论是否可以使用?对于末速度为零的匀减速直线运动,可把它看成逆向的初速度为零的匀加速直线运动,应用比例关系,可使问题简化初速度为零的匀变速直线运动的位移特点如图所示,一小球从 A 点由静止开始沿斜面做匀变速直线运动,若到达 B 点时速度为 v,到达 C 点时速度为 2v,则 AB:AC 等于(? ? ? ? )A . 1:1
B . 1:2
C . 1:3
D . 1:4D初速度为零的匀变速直线运动的位移特点速度、加速度的测量通常比位移的测量要复杂些,而有的时候我们只需比较两个物体运动的加速度,并不需要知道加速度的大小,例如比较两辆汽车的加速性能就是这样。如果已知两个物体在相同时间内从静止开始运动的位移之比,怎样根据运动学的规律由此求出它们的加速度之比?初速度为零的匀变速直线运动的时间特点从运动起点划分为连续相等位移 x,则:位移 x、2x、3x……nx 内的时间之比为?第 1 段位移 x、第 2 段位移 x、第 3 段位移 x 内的时间之比为?v = at初速度为零的匀变速直线运动的时间特点一列火车由静止以恒定的加速度启动出站,设每列车厢的长度相同,不计车厢间隙距离,一观察者站在第一列车厢最前面,他通过测时间估算出第一列车厢尾驶过他时的速度为 v0,则第 n 列车厢尾驶过他时的速度为(? ? ? ? ? )C匀变速直线运动规律:总结速度公式:位移公式:平均速度:v=v0+at
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
