第三章第5节力的分解(共36张PPT)
文档属性
| 名称 | 第三章第5节力的分解(共36张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 431.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-12-10 10:06:53 | ||
图片预览





文档简介
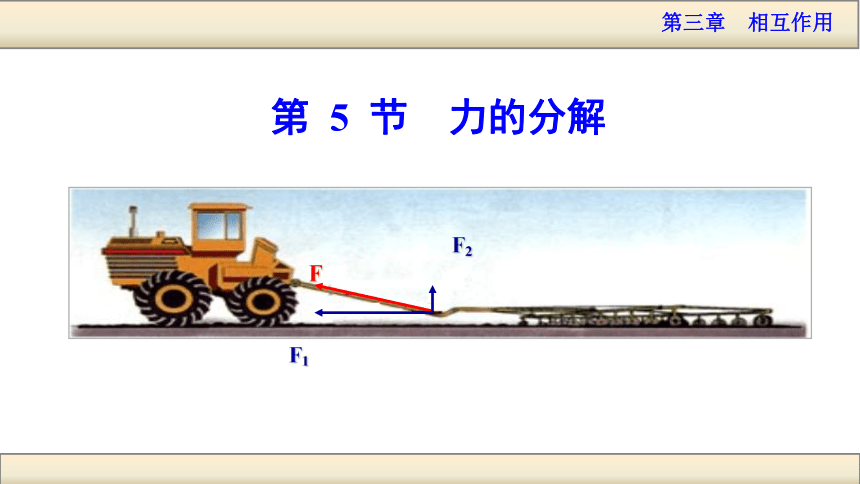
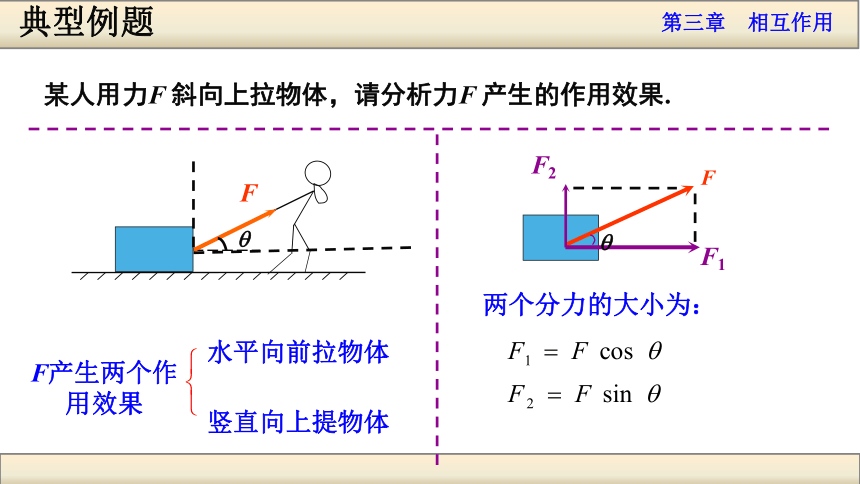
课件36张PPT。F2F1第 5 节 力的分解 一、力的分解求一个已知力的分力叫做力的分解力的分解也遵循力的平行四边形定则,它是力的合成的逆运算.把一个已知力F作为平行四边形的对角线,与力F共点的平行四边形的两个邻边就表示分力F 合力的合成 有唯一解 合力的分解 有无数个解F1F2F1F2F1F2那么沿哪两个方向分解呢?力的实际作用效果 合力的分解F1F2F1F2F1F2 有无数个解力的实际作用效果分解FF1F2q某人用力F 斜向上拉物体,请分析力F 产生的作用效果. 两个分力的大小为:典型例题qF产生两个作用效果两个静止在斜面上的物体,重力都为G,产生的作用效果
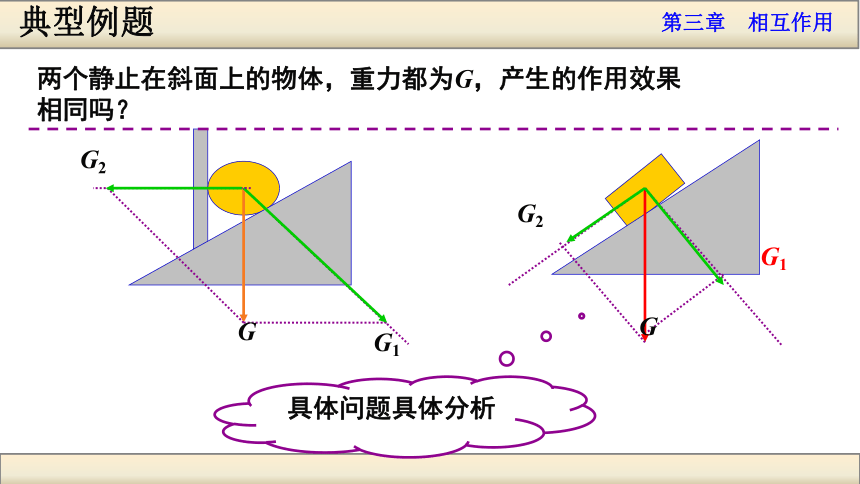
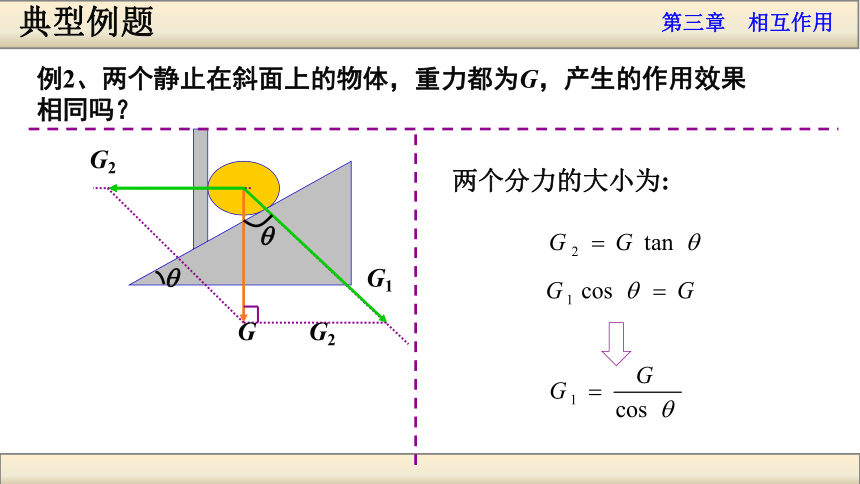
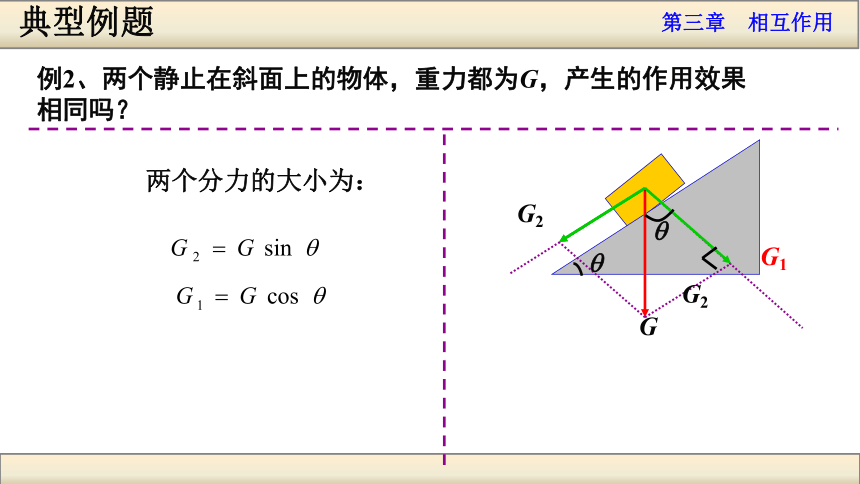
相同吗?典型例题G1G1G2G2GG具体问题具体分析典型例题G1G2GqqG2两个分力的大小为:例2、两个静止在斜面上的物体,重力都为G,产生的作用效果
相同吗?典型例题G1G2GqqG2 两个分力的大小为:例2、两个静止在斜面上的物体,重力都为G,产生的作用效果
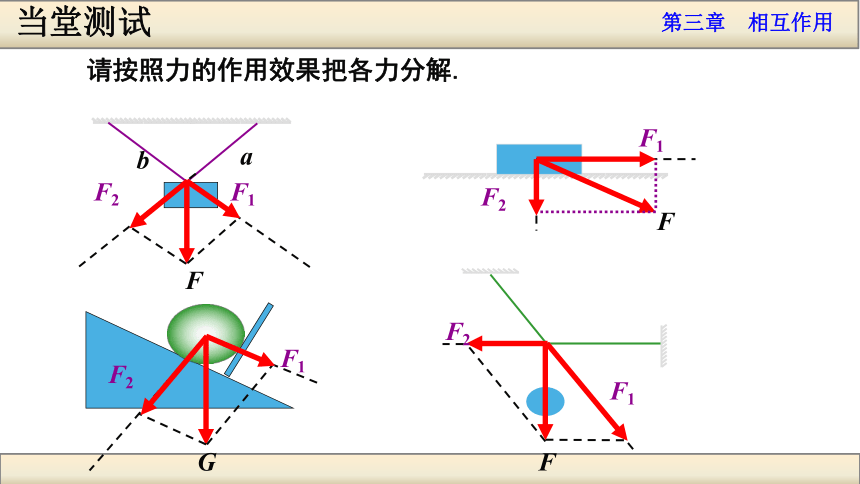
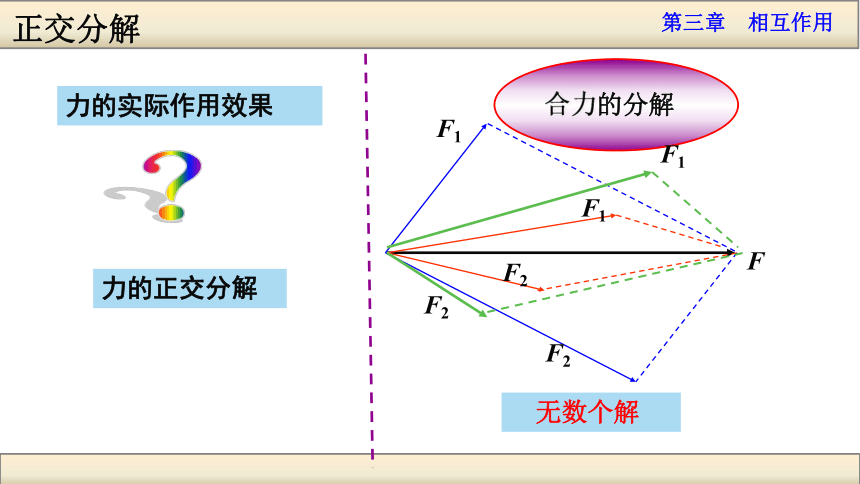
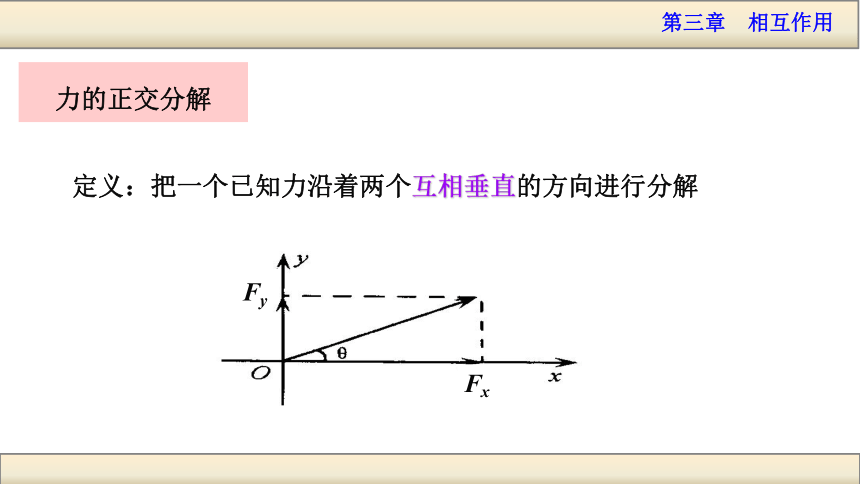
相同吗?ab当堂测试请按照力的作用效果把各力分解.F1F1F1F1F2F2F2F2 合力的分解 无数个解F1F2F1F2F1F2力的实际作用效果?力的正交分解正交分解力的正交分解 定义:把一个已知力沿着两个互相垂直的方向进行分解正交分解步骤:①以共点力的作用点为坐标原点
建立xOy直角坐标系(让尽可能多的力
落在坐标轴上)②分别向坐标轴做垂线,将不在坐标轴上的力分在坐标轴上FqFxFy③利用三角函数求出Fx、Fy,列出每个方向满足的关系O④最后求Fx和Fy的合力FFFxFy某人用力F=20 N 斜向上30°的力拉物体, 请利用正交分解法求水平和竖直两个方向上的分力.两个分力的大小为:典型例题qyx三个共点力F1=20 N、F2=30 N、F3=40 N,它们相互间的夹角为120o,求它们的合力.120o120o120oxyF1=20 NF2=30 NF3=40 NF2xF2yF3yF3x F2两个分力的大小为:典型例题 F3两个分力的大小为:典型例题三个共点力F1=20 N、F2=30 N、F3=40 N,它们相互间的夹角为120o,求它们的合力.120o120o120oxyF1=20 NF2=30 NF3=40 NF2xF2yF3yF3x 两个方向的合力的大小为:典型例题120o120o120oxyF1=20 NF2=30 NF3=40 NF2xF2yF3yF3x三个共点力F1=20 N、F2=30 N、F3=40 N,它们相互间的夹角为120o,求它们的合力. 三个力合力的大小为:典型例题三个共点力F1=20 N、F2=30 N、F3=40 N,它们相互间的夹角为120o,求它们的合力.120o120o120oxyF1=20 NF2=30 NF3=40 NF2xF2yF3yF3xFFxFyF在水平方向分力的大小为:qyxfG当堂测试某人用力F=40 N 斜向上60°的力拉物体向右运动,已知物体所受的滑动摩擦力为10 N.求物体在水平方向所受的合力为多少?FFxFy则在水平方向上的合力为:qyxfG当堂测试某人用力F=40 N 斜向上60°的力拉物体向右运动,已知物体所受的滑动摩擦力为10 N.求物体在水平方向所受的合力为多少?4.一物体受到三个共点力的作用,其中F1=20 N,F2=4 N,F3=8 N,已知F3沿水平方向F2在竖直方向,F1与水平方向夹角为37°,求三个力的合力.当堂测试F1F2F3yxqF1xF1y F1两个分力的大小为:当堂测试 两个方向的合力大小为:F1F2F3yxqF1xF1y一物体受到三个共点力的作用,其中F1=20 N,F2=4 N,F3=8 N,已知F3沿水平方向F2在竖直方向,F1与水平方向夹角为37°,求三个力的合力.当堂测试FF合yyxF合x 三个力的合力大小为: 与水平方向成45°角一物体受到三个共点力的作用,其中F1=20 N,F2=4 N,F3=8 N,已知F3沿水平方向F2在竖直方向,F1与水平方向夹角为37°,求三个力的合力.问题1、将一个已知力分解,其结果的讨论1)已知两个分力的方向——2)已知一个分力的大小和方向——唯一解唯一解问题2、若已知一个分力F1的大小和另一分力F2的方向
(即已知F2和F的夹角θ),将一已知力F分解,
其结果有多少种可能?1)F1< Fsinθ……无解2)F1= Fsinθ……一解3)Fsinθ 解,其结果有多少种可能?问题4、力分解中的最值问题?F2min =F sinθF1=FcosθF=F1cos θF2min =F 1sin θ矢量相加法则(1)平行四边形定则
(2)三角形定则
将两个矢量首尾相接,从一个矢量的箭尾指向另一个矢量的箭头的有向线段就是这两个矢量的合矢量。
(3)三角形定则与平行四边形定则在本质上是一样的。
相同吗?典型例题G1G1G2G2GG具体问题具体分析典型例题G1G2GqqG2两个分力的大小为:例2、两个静止在斜面上的物体,重力都为G,产生的作用效果
相同吗?典型例题G1G2GqqG2 两个分力的大小为:例2、两个静止在斜面上的物体,重力都为G,产生的作用效果
相同吗?ab当堂测试请按照力的作用效果把各力分解.F1F1F1F1F2F2F2F2 合力的分解 无数个解F1F2F1F2F1F2力的实际作用效果?力的正交分解正交分解力的正交分解 定义:把一个已知力沿着两个互相垂直的方向进行分解正交分解步骤:①以共点力的作用点为坐标原点
建立xOy直角坐标系(让尽可能多的力
落在坐标轴上)②分别向坐标轴做垂线,将不在坐标轴上的力分在坐标轴上FqFxFy③利用三角函数求出Fx、Fy,列出每个方向满足的关系O④最后求Fx和Fy的合力FFFxFy某人用力F=20 N 斜向上30°的力拉物体, 请利用正交分解法求水平和竖直两个方向上的分力.两个分力的大小为:典型例题qyx三个共点力F1=20 N、F2=30 N、F3=40 N,它们相互间的夹角为120o,求它们的合力.120o120o120oxyF1=20 NF2=30 NF3=40 NF2xF2yF3yF3x F2两个分力的大小为:典型例题 F3两个分力的大小为:典型例题三个共点力F1=20 N、F2=30 N、F3=40 N,它们相互间的夹角为120o,求它们的合力.120o120o120oxyF1=20 NF2=30 NF3=40 NF2xF2yF3yF3x 两个方向的合力的大小为:典型例题120o120o120oxyF1=20 NF2=30 NF3=40 NF2xF2yF3yF3x三个共点力F1=20 N、F2=30 N、F3=40 N,它们相互间的夹角为120o,求它们的合力. 三个力合力的大小为:典型例题三个共点力F1=20 N、F2=30 N、F3=40 N,它们相互间的夹角为120o,求它们的合力.120o120o120oxyF1=20 NF2=30 NF3=40 NF2xF2yF3yF3xFFxFyF在水平方向分力的大小为:qyxfG当堂测试某人用力F=40 N 斜向上60°的力拉物体向右运动,已知物体所受的滑动摩擦力为10 N.求物体在水平方向所受的合力为多少?FFxFy则在水平方向上的合力为:qyxfG当堂测试某人用力F=40 N 斜向上60°的力拉物体向右运动,已知物体所受的滑动摩擦力为10 N.求物体在水平方向所受的合力为多少?4.一物体受到三个共点力的作用,其中F1=20 N,F2=4 N,F3=8 N,已知F3沿水平方向F2在竖直方向,F1与水平方向夹角为37°,求三个力的合力.当堂测试F1F2F3yxqF1xF1y F1两个分力的大小为:当堂测试 两个方向的合力大小为:F1F2F3yxqF1xF1y一物体受到三个共点力的作用,其中F1=20 N,F2=4 N,F3=8 N,已知F3沿水平方向F2在竖直方向,F1与水平方向夹角为37°,求三个力的合力.当堂测试FF合yyxF合x 三个力的合力大小为: 与水平方向成45°角一物体受到三个共点力的作用,其中F1=20 N,F2=4 N,F3=8 N,已知F3沿水平方向F2在竖直方向,F1与水平方向夹角为37°,求三个力的合力.问题1、将一个已知力分解,其结果的讨论1)已知两个分力的方向——2)已知一个分力的大小和方向——唯一解唯一解问题2、若已知一个分力F1的大小和另一分力F2的方向
(即已知F2和F的夹角θ),将一已知力F分解,
其结果有多少种可能?1)F1< Fsinθ……无解2)F1= Fsinθ……一解3)Fsinθ
(2)三角形定则
将两个矢量首尾相接,从一个矢量的箭尾指向另一个矢量的箭头的有向线段就是这两个矢量的合矢量。
(3)三角形定则与平行四边形定则在本质上是一样的。
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
