四年级下册数学试题分析 二、生活中的多边形—多边形的面积 青岛版(五年制) 含答案
文档属性
| 名称 | 四年级下册数学试题分析 二、生活中的多边形—多边形的面积 青岛版(五年制) 含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 98.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 00:00:00 | ||
图片预览

文档简介
二、生活中的多边形—多边形的面积
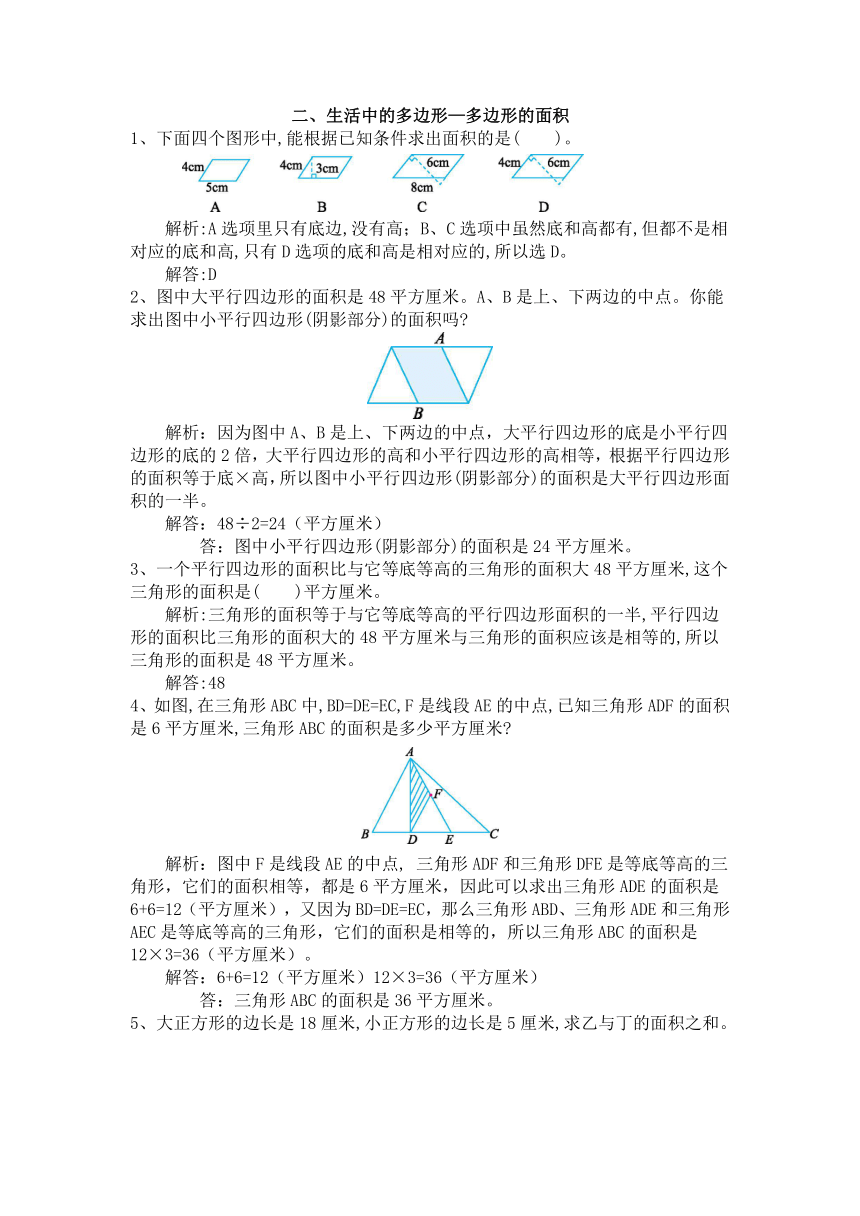
1、下面四个图形中,能根据已知条件求出面积的是( )。
解析:A选项里只有底边,没有高;B、C选项中虽然底和高都有,但都不是相对应的底和高,只有D选项的底和高是相对应的,所以选D。
解答:D
2、图中大平行四边形的面积是48平方厘米。A、B是上、下两边的中点。你能求出图中小平行四边形(阴影部分)的面积吗?
解析:因为图中A、B是上、下两边的中点,大平行四边形的底是小平行四边形的底的2倍,大平行四边形的高和小平行四边形的高相等,根据平行四边形的面积等于底×高,所以图中小平行四边形(阴影部分)的面积是大平行四边形面积的一半。
解答:48÷2=24(平方厘米)
答:图中小平行四边形(阴影部分)的面积是24平方厘米。
3、一个平行四边形的面积比与它等底等高的三角形的面积大48平方厘米,这个三角形的面积是( )平方厘米。
解析:三角形的面积等于与它等底等高的平行四边形面积的一半,平行四边形的面积比三角形的面积大的48平方厘米与三角形的面积应该是相等的,所以三角形的面积是48平方厘米。
解答:48
4、如图,在三角形ABC中,BD=DE=EC,F是线段AE的中点,已知三角形ADF的面积是6平方厘米,三角形ABC的面积是多少平方厘米?
解析:图中F是线段AE的中点, 三角形ADF和三角形DFE是等底等高的三角形,它们的面积相等,都是6平方厘米,因此可以求出三角形ADE的面积是6+6=12(平方厘米),又因为BD=DE=EC,那么三角形ABD、三角形ADE和三角形AEC是等底等高的三角形,它们的面积是相等的,所以三角形ABC的面积是12×3=36(平方厘米)。
解答:6+6=12(平方厘米)12×3=36(平方厘米)
答:三角形ABC的面积是36平方厘米。
5、大正方形的边长是18厘米,小正方形的边长是5厘米,求乙与丁的面积之和。
解析:乙和丁两个梯形的上底和下底分别相等,分别是5厘米和18厘米,它们各自的高虽不确定,但两个梯形的高的和是18-5=13(厘米)。所以利用乘法分配律就可以求出两个梯形的面积之和。
解答:乙高+丁高=18-5=13(厘米)
(18+5)×乙高÷2+(18+5)×丁高÷2
=(18+5)×(乙高+丁高)÷2
=23×13÷2
=149.5(平方厘米)
答:乙和丁的面积之和是149.5平方厘米。
6、下图是一张直角梯形的纸,把纸的一角如图那样折叠,求阴影部分的面积。(单位:厘米)
解析:图中是把直角梯形纸的一角折叠,那么两个白色的三角形是完全相等的,所以三角形中较长的直角边7厘米就是梯形的高,阴影部分的面积可以从右边梯形面积中减去一个三角形的面积。
解答:(5+16)×7÷2-4×7÷2
=21×7÷2-14
=73.5-14
=59.5(平方厘米)
答:阴影部分的面积59.5平方厘米。
7、下图中阴影部分的面积是多大?
解析:图中两个阴影三角形的底都是10cm,高相加是6cm,所以它们的面积的和是长方形面积的一半。
解答:10×6÷2=30(cm2)
8、下图是由大小两个正方形组成的。求阴影部分的面积。(单位:厘米)
解析:图中有大小两个正方形,阴影部分的面积就是从两个正方形面积和里去掉白色大梯形的面积,从图中可以找出白色大梯形的上底是6-3=3厘米,下底是7厘米,高是6+7=13厘米,白色大梯形的面积是(3+7)×13÷2=65(平方厘米),两个正方形的面积和是7×7+6×6=85(平方厘米)所以阴影部分的面积是85-65=20(平方厘米)。
解答:6-3=3(厘米) 6+7=13(厘米)
(3+7)×13÷2=65(平方厘米)
7×7+6×6=85(平方厘米)
85-65=20(平方厘米)
答:阴影部分的面积是20平方厘米。
1、下面四个图形中,能根据已知条件求出面积的是( )。
解析:A选项里只有底边,没有高;B、C选项中虽然底和高都有,但都不是相对应的底和高,只有D选项的底和高是相对应的,所以选D。
解答:D
2、图中大平行四边形的面积是48平方厘米。A、B是上、下两边的中点。你能求出图中小平行四边形(阴影部分)的面积吗?
解析:因为图中A、B是上、下两边的中点,大平行四边形的底是小平行四边形的底的2倍,大平行四边形的高和小平行四边形的高相等,根据平行四边形的面积等于底×高,所以图中小平行四边形(阴影部分)的面积是大平行四边形面积的一半。
解答:48÷2=24(平方厘米)
答:图中小平行四边形(阴影部分)的面积是24平方厘米。
3、一个平行四边形的面积比与它等底等高的三角形的面积大48平方厘米,这个三角形的面积是( )平方厘米。
解析:三角形的面积等于与它等底等高的平行四边形面积的一半,平行四边形的面积比三角形的面积大的48平方厘米与三角形的面积应该是相等的,所以三角形的面积是48平方厘米。
解答:48
4、如图,在三角形ABC中,BD=DE=EC,F是线段AE的中点,已知三角形ADF的面积是6平方厘米,三角形ABC的面积是多少平方厘米?
解析:图中F是线段AE的中点, 三角形ADF和三角形DFE是等底等高的三角形,它们的面积相等,都是6平方厘米,因此可以求出三角形ADE的面积是6+6=12(平方厘米),又因为BD=DE=EC,那么三角形ABD、三角形ADE和三角形AEC是等底等高的三角形,它们的面积是相等的,所以三角形ABC的面积是12×3=36(平方厘米)。
解答:6+6=12(平方厘米)12×3=36(平方厘米)
答:三角形ABC的面积是36平方厘米。
5、大正方形的边长是18厘米,小正方形的边长是5厘米,求乙与丁的面积之和。
解析:乙和丁两个梯形的上底和下底分别相等,分别是5厘米和18厘米,它们各自的高虽不确定,但两个梯形的高的和是18-5=13(厘米)。所以利用乘法分配律就可以求出两个梯形的面积之和。
解答:乙高+丁高=18-5=13(厘米)
(18+5)×乙高÷2+(18+5)×丁高÷2
=(18+5)×(乙高+丁高)÷2
=23×13÷2
=149.5(平方厘米)
答:乙和丁的面积之和是149.5平方厘米。
6、下图是一张直角梯形的纸,把纸的一角如图那样折叠,求阴影部分的面积。(单位:厘米)
解析:图中是把直角梯形纸的一角折叠,那么两个白色的三角形是完全相等的,所以三角形中较长的直角边7厘米就是梯形的高,阴影部分的面积可以从右边梯形面积中减去一个三角形的面积。
解答:(5+16)×7÷2-4×7÷2
=21×7÷2-14
=73.5-14
=59.5(平方厘米)
答:阴影部分的面积59.5平方厘米。
7、下图中阴影部分的面积是多大?
解析:图中两个阴影三角形的底都是10cm,高相加是6cm,所以它们的面积的和是长方形面积的一半。
解答:10×6÷2=30(cm2)
8、下图是由大小两个正方形组成的。求阴影部分的面积。(单位:厘米)
解析:图中有大小两个正方形,阴影部分的面积就是从两个正方形面积和里去掉白色大梯形的面积,从图中可以找出白色大梯形的上底是6-3=3厘米,下底是7厘米,高是6+7=13厘米,白色大梯形的面积是(3+7)×13÷2=65(平方厘米),两个正方形的面积和是7×7+6×6=85(平方厘米)所以阴影部分的面积是85-65=20(平方厘米)。
解答:6-3=3(厘米) 6+7=13(厘米)
(3+7)×13÷2=65(平方厘米)
7×7+6×6=85(平方厘米)
85-65=20(平方厘米)
答:阴影部分的面积是20平方厘米。
