人教版八年级上数学教学讲义,复习补习资料(巩固练习):20【提高】《全等三角形》全章复习与巩固含答案
文档属性
| 名称 | 人教版八年级上数学教学讲义,复习补习资料(巩固练习):20【提高】《全等三角形》全章复习与巩固含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 161.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-09 00:00:00 | ||
图片预览


文档简介
全等三角形全章复习与巩固(提高)
【学习目标】
1. 了解全等三角形的概念和性质,能够准确地辨认全等三角形中的对应元素;
2.探索三角形全等的判定方法,能利用三角形全等进行证明,掌握综合法证明的格式;
3.会作角的平分线,了解角的平分线的性质,能利用三角形全等证明角的平分线的性质, 会利用角的平分线的性质进行证明.
【知识网络】
【巩固练习】
一.选择题
1.(2019春?龙岗区期末)如图,在△ABC与△DEF中,给出以下六个条件:
(1)AB=DE;(2)BC=EF;(3)AC=DF;(4)∠A=∠D;(5)∠B=∠E;(6)∠C=∠F.
以其中三个作为已知条件,不能判断△ABC与△DEF全等的是( )
A.(1)(5)(2) B.(1)(2)(3) C. (2)(3)(4) D. (4)(6)(1)
2. (2019?深圳二模)两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=AC?BD,其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
3. 如图, AB∥CD, AC∥BD, AD与BC交于O, AE⊥BC于E, DF⊥BC于F, 那么图中全等的三角形有( )
A. 5对 B. 6对 C. 7对 D. 8对
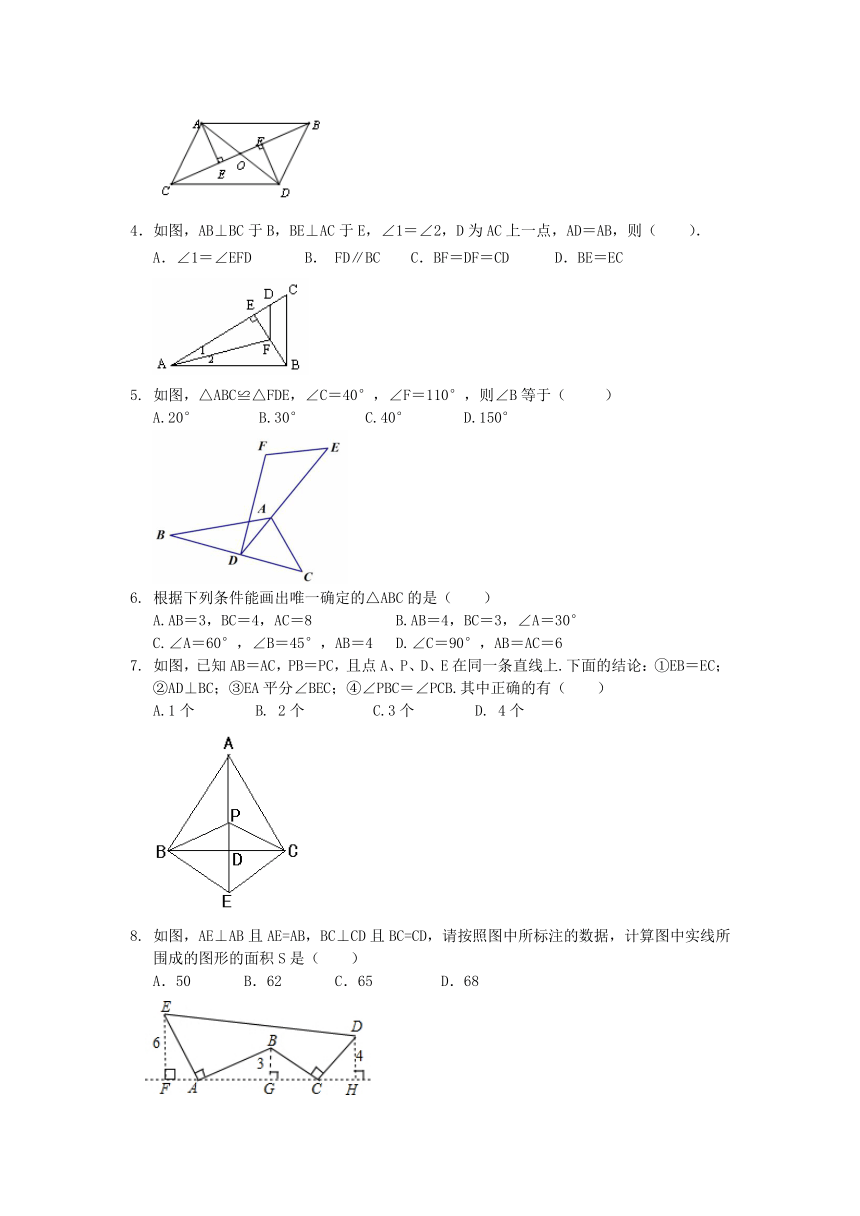
4.如图,AB⊥BC于B,BE⊥AC于E,∠1=∠2,D为AC上一点,AD=AB,则( ).
A.∠1=∠EFD B. FD∥BC C.BF=DF=CD D.BE=EC
5. 如图,△ABC≌△FDE,∠C=40°,∠F=110°,则∠B等于( )
A.20° B.30° C.40° D.150°
6. 根据下列条件能画出唯一确定的△ABC的是( )
A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°
C.∠A=60°,∠B=45°,AB=4 D.∠C=90°,AB=AC=6
7. 如图,已知AB=AC,PB=PC,且点A、P、D、E在同一条直线上.下面的结论:①EB=EC;②AD⊥BC;③EA平分∠BEC;④∠PBC=∠PCB.其中正确的有( )
A.1个 B. 2个 C.3个 D. 4个
8. 如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
A.50 B.62 C.65 D.68
二.填空题
9. 在平面直角坐标系中,已知点A(1,2),B(5,5),C(5,2),存在点E,使△ACE和△ACB全等,写出所有满足条件的E点的坐标 .
10. 如图,△ABC中,H是高AD、BE的交点,且BH=AC,则∠ABC=________.
11. 在△ABC中,∠C=90°,AC=BC,AD平分∠BAC,DE⊥AB于E.若AB=20cm,则△DBE的周长为_________.
12. 如图,△ABC中,∠C=90°,ED∥AB,∠1=∠2,若CD=1.3,则点D到AB边的距离是_______.
13. 如图,Rt△ABC中,∠B=90°,若点O到三角形三边的距离相等,则∠AOC=_________.
14. 如图,BA⊥AC,CD∥AB,BC=DE,且BC⊥DE.若AB=2,CD=6,则AE=_______.
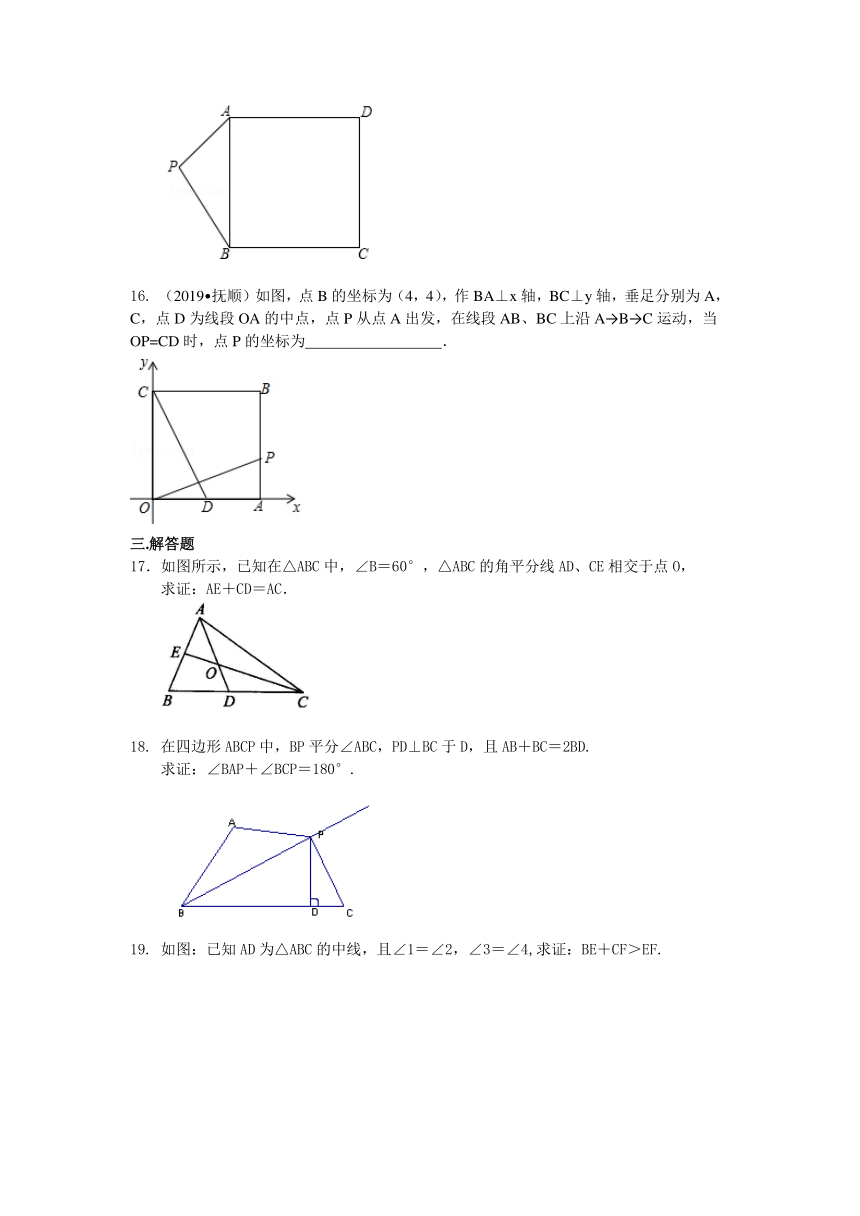
15. (2019?黄冈中学自主招生)如图所示,已知P是正方形ABCD外一点,且PA=3,PB=4,则PC的最大值是 .
16. (2019?抚顺)如图,点B的坐标为(4,4),作BA⊥x轴,BC⊥y轴,垂足分别为A,C,点D为线段OA的中点,点P从点A出发,在线段AB、BC上沿A→B→C运动,当OP=CD时,点P的坐标为 .
三.解答题
17.如图所示,已知在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,
求证:AE+CD=AC.
18. 在四边形ABCP中,BP平分∠ABC,PD⊥BC于D,且AB+BC=2BD.
求证:∠BAP+∠BCP=180°.
19. 如图:已知AD为△ABC的中线,且∠1=∠2,∠3=∠4,求证:BE+CF>EF.
20.(2019?于洪区一模)如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
【答案与解析】
一.选择题
1. 【答案】C;
【解析】解:A、(1)(5)(2)符合“SAS”,能判断△ABC与△DEF全等,故本选项错误;
B、(1)(2)(3)符合“SSS”,能判断△ABC与△DEF全等,故本选项错误;
C、(2)(3)(4),是边边角,不能判断△ABC与△DEF全等,故本选项正确;
D、(4)(6)(1)符合“AAS”,能判断△ABC与△DEF全等,故本选项错误.
故选C.
2. 【答案】D;
【解析】△ABD≌△CBD(SSS),故①正确;△AOD≌△COD(SAS),
∴∠AOD=∠COD=90°,AO=OC,∴AC⊥DB,故②正确;
四边形ABCD的面积==AC?BD,
故③正确;故选D.
3. 【答案】C;
4. 【答案】B ;
【解析】证△ADF≌△ABF,则∠ABF=∠ADF=∠ACB,所以FD∥BC.
5. 【答案】B;
【解析】∠C=∠E,∠B=∠FDE=180°-110°-40°=30°.
6. 【答案】C;
【解析】A项构不成三角形,B项是SSA,D项斜边和直角边一样长,是不可能的.
7. 【答案】D;
8. 【答案】A;
【解析】易证∴△EFA≌△ABG得AF=BG,AG=EF.同理证得△BGC≌△DHC得GC=DH,CH=BG.故FH=FA+AG+GC+CH=3+6+4+3=16,故S=(6+4)×16-3×4-6×3=50.
二.填空题
9. 【答案】(1,5)或(1,-1)或(5,-1) ;
10.【答案】45°;
【解析】Rt△BDH≌Rt△ADC,BD=AD.
11.【答案】20;
【解析】BC=AC=AE,△DBE的周长等于AB.
12.【答案】1.3;
【解析】AD是∠BAC的平分线,点D到AB的距离等于DC.
13.【答案】135°;
【解析】点O为角平分线的交点,∠AOC=180°-(∠BAC+∠BCA)=135°.
14.【答案】4;
【解析】证△ABC≌△CED.
15.【答案】3+4;
【解析】解:如图,过点B作BE⊥BP,且BE=PB,连接AE、PE、PC,
则PE=PB=4,
∵∠ABE=∠ABP+90°,∠CBP=∠ABP+90°,
∴∠ABE=∠CBP,
在△ABE和△CBP中,
,
∴△ABE≌△CBP(SAS),
∴AE=PC,
由两点之间线段最短可知,点A、P、E三点共线时AE最大,
此时AE=AP+PE=3+4,
所以,PC的最大值是3+4.
故答案为:3+4.
16.【答案】(2,4)或(4,2);
【解析】①当点P在正方形的边AB上时,Rt△OCD≌Rt△OAP,∴OD=AP,∵点D是OA中点,∴OD=AD=OA,∴AP=AB=2,∴P(4,2),②当点P在正方形的边BC上时,同①的方法,得出CP=BC=2,∴P(2,4).
三.解答题
17.【解析】
证明:如图所示,在AC上取点F,使AF=AE,连接OF,
在△AEO和△AFO中,
∴ △AEO≌△AFO(SAS).
∴ ∠EOA=∠FOA.
∵ ∠B=60°,
∴ ∠AOC=180°-(∠OAC+∠OCA)
=180°-(∠BAC+∠BCA)
=180°-(180°-60°)
=120°.
∴ ∠AOE=∠AOF=∠COF=∠DOC=60°.
在△COD和△COF中,
∴ △COD≌△COF(ASA).
∴ CD=CF.
∴ AE+CD=AF+CF=AC.
18.【解析】
证明:过点P作PE⊥AB,交BA的延长线于E,
∵ BP平分∠ABC,PD⊥BC ,PE⊥AB,
∴PE=PD
在Rt△PBE与Rt△PBD中,BP=BP,PE=PD
∴Rt△PBE≌Rt△PBD(HL)
∴BE=BD
又∵AB+BC=2BD.
∴AB+BD+DC=2BD,即AB+DC=BD
∴AE=DC
由(SAS)可证Rt△PEA≌Rt△PDC,
∴∠PAE=∠PCD
∵∠BAP+∠PAE=180°
∴∠BAP+∠BCP=180°.
19.【解析】
证明:在DA上截取DN=DB,连接NE,NF,则DN=DC, 在△DBE和△DNE中: ∴△DBE≌△DNE (SAS) ∴BE=NE(全等三角形对应边相等) 同理可得:CF=NF 在△EFN中EN+FN>EF(三角形两边之和大于第三边) ∴BE+CF>EF.
20.【解析】
证明:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
又∵AB=AC,
∴△DAB≌△FAC,
∴CF=BD,∠B=∠ACF,
∴∠ACB+∠ACF=90°,即CF⊥BD.
故答案为:CF⊥BD,CF=BD.
②当点D在BC的延长线上时①的结论仍成立.
由正方形ADEF得AD=AF,∠DAF=90°.
∵∠BAC=90°,
∴∠DAF=∠BAC,
∴∠DAB=∠FAC,
又∵AB=AC,
∴△DAB≌△FAC,
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACF=45°,
∴∠BCF=∠ACB+∠ACF=90°.
即CF⊥BD.
(2)当∠ACB=45°时,CF⊥BD(如图).
理由:过点A作AG⊥AC交CB的延长线于点G,
则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°﹣∠ACB,
∴∠AGC=90°﹣45°=45°,
∴∠ACB=∠AGC=45°,
∴AC=AG,
∵∠DAG=∠FAC(同角的余角相等),AD=AF,
∴△GAD≌△CAF,
∴∠ACF=∠AGC=45°,
∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.
【学习目标】
1. 了解全等三角形的概念和性质,能够准确地辨认全等三角形中的对应元素;
2.探索三角形全等的判定方法,能利用三角形全等进行证明,掌握综合法证明的格式;
3.会作角的平分线,了解角的平分线的性质,能利用三角形全等证明角的平分线的性质, 会利用角的平分线的性质进行证明.
【知识网络】
【巩固练习】
一.选择题
1.(2019春?龙岗区期末)如图,在△ABC与△DEF中,给出以下六个条件:
(1)AB=DE;(2)BC=EF;(3)AC=DF;(4)∠A=∠D;(5)∠B=∠E;(6)∠C=∠F.
以其中三个作为已知条件,不能判断△ABC与△DEF全等的是( )
A.(1)(5)(2) B.(1)(2)(3) C. (2)(3)(4) D. (4)(6)(1)
2. (2019?深圳二模)两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=AC?BD,其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
3. 如图, AB∥CD, AC∥BD, AD与BC交于O, AE⊥BC于E, DF⊥BC于F, 那么图中全等的三角形有( )
A. 5对 B. 6对 C. 7对 D. 8对
4.如图,AB⊥BC于B,BE⊥AC于E,∠1=∠2,D为AC上一点,AD=AB,则( ).
A.∠1=∠EFD B. FD∥BC C.BF=DF=CD D.BE=EC
5. 如图,△ABC≌△FDE,∠C=40°,∠F=110°,则∠B等于( )
A.20° B.30° C.40° D.150°
6. 根据下列条件能画出唯一确定的△ABC的是( )
A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°
C.∠A=60°,∠B=45°,AB=4 D.∠C=90°,AB=AC=6
7. 如图,已知AB=AC,PB=PC,且点A、P、D、E在同一条直线上.下面的结论:①EB=EC;②AD⊥BC;③EA平分∠BEC;④∠PBC=∠PCB.其中正确的有( )
A.1个 B. 2个 C.3个 D. 4个
8. 如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
A.50 B.62 C.65 D.68
二.填空题
9. 在平面直角坐标系中,已知点A(1,2),B(5,5),C(5,2),存在点E,使△ACE和△ACB全等,写出所有满足条件的E点的坐标 .
10. 如图,△ABC中,H是高AD、BE的交点,且BH=AC,则∠ABC=________.
11. 在△ABC中,∠C=90°,AC=BC,AD平分∠BAC,DE⊥AB于E.若AB=20cm,则△DBE的周长为_________.
12. 如图,△ABC中,∠C=90°,ED∥AB,∠1=∠2,若CD=1.3,则点D到AB边的距离是_______.
13. 如图,Rt△ABC中,∠B=90°,若点O到三角形三边的距离相等,则∠AOC=_________.
14. 如图,BA⊥AC,CD∥AB,BC=DE,且BC⊥DE.若AB=2,CD=6,则AE=_______.
15. (2019?黄冈中学自主招生)如图所示,已知P是正方形ABCD外一点,且PA=3,PB=4,则PC的最大值是 .
16. (2019?抚顺)如图,点B的坐标为(4,4),作BA⊥x轴,BC⊥y轴,垂足分别为A,C,点D为线段OA的中点,点P从点A出发,在线段AB、BC上沿A→B→C运动,当OP=CD时,点P的坐标为 .
三.解答题
17.如图所示,已知在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,
求证:AE+CD=AC.
18. 在四边形ABCP中,BP平分∠ABC,PD⊥BC于D,且AB+BC=2BD.
求证:∠BAP+∠BCP=180°.
19. 如图:已知AD为△ABC的中线,且∠1=∠2,∠3=∠4,求证:BE+CF>EF.
20.(2019?于洪区一模)如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
【答案与解析】
一.选择题
1. 【答案】C;
【解析】解:A、(1)(5)(2)符合“SAS”,能判断△ABC与△DEF全等,故本选项错误;
B、(1)(2)(3)符合“SSS”,能判断△ABC与△DEF全等,故本选项错误;
C、(2)(3)(4),是边边角,不能判断△ABC与△DEF全等,故本选项正确;
D、(4)(6)(1)符合“AAS”,能判断△ABC与△DEF全等,故本选项错误.
故选C.
2. 【答案】D;
【解析】△ABD≌△CBD(SSS),故①正确;△AOD≌△COD(SAS),
∴∠AOD=∠COD=90°,AO=OC,∴AC⊥DB,故②正确;
四边形ABCD的面积==AC?BD,
故③正确;故选D.
3. 【答案】C;
4. 【答案】B ;
【解析】证△ADF≌△ABF,则∠ABF=∠ADF=∠ACB,所以FD∥BC.
5. 【答案】B;
【解析】∠C=∠E,∠B=∠FDE=180°-110°-40°=30°.
6. 【答案】C;
【解析】A项构不成三角形,B项是SSA,D项斜边和直角边一样长,是不可能的.
7. 【答案】D;
8. 【答案】A;
【解析】易证∴△EFA≌△ABG得AF=BG,AG=EF.同理证得△BGC≌△DHC得GC=DH,CH=BG.故FH=FA+AG+GC+CH=3+6+4+3=16,故S=(6+4)×16-3×4-6×3=50.
二.填空题
9. 【答案】(1,5)或(1,-1)或(5,-1) ;
10.【答案】45°;
【解析】Rt△BDH≌Rt△ADC,BD=AD.
11.【答案】20;
【解析】BC=AC=AE,△DBE的周长等于AB.
12.【答案】1.3;
【解析】AD是∠BAC的平分线,点D到AB的距离等于DC.
13.【答案】135°;
【解析】点O为角平分线的交点,∠AOC=180°-(∠BAC+∠BCA)=135°.
14.【答案】4;
【解析】证△ABC≌△CED.
15.【答案】3+4;
【解析】解:如图,过点B作BE⊥BP,且BE=PB,连接AE、PE、PC,
则PE=PB=4,
∵∠ABE=∠ABP+90°,∠CBP=∠ABP+90°,
∴∠ABE=∠CBP,
在△ABE和△CBP中,
,
∴△ABE≌△CBP(SAS),
∴AE=PC,
由两点之间线段最短可知,点A、P、E三点共线时AE最大,
此时AE=AP+PE=3+4,
所以,PC的最大值是3+4.
故答案为:3+4.
16.【答案】(2,4)或(4,2);
【解析】①当点P在正方形的边AB上时,Rt△OCD≌Rt△OAP,∴OD=AP,∵点D是OA中点,∴OD=AD=OA,∴AP=AB=2,∴P(4,2),②当点P在正方形的边BC上时,同①的方法,得出CP=BC=2,∴P(2,4).
三.解答题
17.【解析】
证明:如图所示,在AC上取点F,使AF=AE,连接OF,
在△AEO和△AFO中,
∴ △AEO≌△AFO(SAS).
∴ ∠EOA=∠FOA.
∵ ∠B=60°,
∴ ∠AOC=180°-(∠OAC+∠OCA)
=180°-(∠BAC+∠BCA)
=180°-(180°-60°)
=120°.
∴ ∠AOE=∠AOF=∠COF=∠DOC=60°.
在△COD和△COF中,
∴ △COD≌△COF(ASA).
∴ CD=CF.
∴ AE+CD=AF+CF=AC.
18.【解析】
证明:过点P作PE⊥AB,交BA的延长线于E,
∵ BP平分∠ABC,PD⊥BC ,PE⊥AB,
∴PE=PD
在Rt△PBE与Rt△PBD中,BP=BP,PE=PD
∴Rt△PBE≌Rt△PBD(HL)
∴BE=BD
又∵AB+BC=2BD.
∴AB+BD+DC=2BD,即AB+DC=BD
∴AE=DC
由(SAS)可证Rt△PEA≌Rt△PDC,
∴∠PAE=∠PCD
∵∠BAP+∠PAE=180°
∴∠BAP+∠BCP=180°.
19.【解析】
证明:在DA上截取DN=DB,连接NE,NF,则DN=DC, 在△DBE和△DNE中: ∴△DBE≌△DNE (SAS) ∴BE=NE(全等三角形对应边相等) 同理可得:CF=NF 在△EFN中EN+FN>EF(三角形两边之和大于第三边) ∴BE+CF>EF.
20.【解析】
证明:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
又∵AB=AC,
∴△DAB≌△FAC,
∴CF=BD,∠B=∠ACF,
∴∠ACB+∠ACF=90°,即CF⊥BD.
故答案为:CF⊥BD,CF=BD.
②当点D在BC的延长线上时①的结论仍成立.
由正方形ADEF得AD=AF,∠DAF=90°.
∵∠BAC=90°,
∴∠DAF=∠BAC,
∴∠DAB=∠FAC,
又∵AB=AC,
∴△DAB≌△FAC,
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACF=45°,
∴∠BCF=∠ACB+∠ACF=90°.
即CF⊥BD.
(2)当∠ACB=45°时,CF⊥BD(如图).
理由:过点A作AG⊥AC交CB的延长线于点G,
则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°﹣∠ACB,
∴∠AGC=90°﹣45°=45°,
∴∠ACB=∠AGC=45°,
∴AC=AG,
∵∠DAG=∠FAC(同角的余角相等),AD=AF,
∴△GAD≌△CAF,
∴∠ACF=∠AGC=45°,
∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.
