沪教版物理共同必修1第4章 怎样求合力与分力4.2 怎样分解力 (课件 共20张PPT)
文档属性
| 名称 | 沪教版物理共同必修1第4章 怎样求合力与分力4.2 怎样分解力 (课件 共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-12-10 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
怎样分解力
苏通长江公路大桥
斜拉桥的钢索对桥面产生的是怎样的作用?
大桥的引桥为什么要绕这么大的圈?
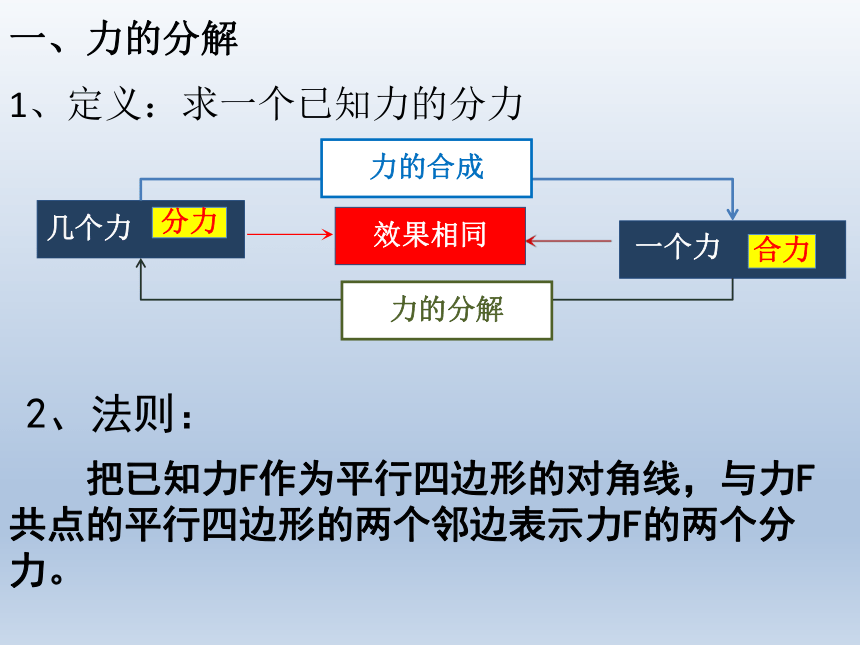
几个力
效果相同
一个力
分力
合力
力的分解
力的合成
一、力的分解
把已知力F作为平行四边形的对角线,与力F共点的平行四边形的两个邻边表示力F的两个分力。
2、法则:
1、定义:求一个已知力的分力
不加限制条件,一个力可分解为无数组不同的分力。
F
由一条对角线可以画出多少个平行四边形?
斜拉桥上一根钢索对桥面的作用力的分解
θ
O
F
F1
F2
F
按效果分解的一般步骤:
1、根据力F的作用效果,画出两个分力的方向;
2、把力F作为对角线,画出平行四边形,得出分力;
3、求解分力的大小和方向。
二、力的分解方法
按照效果分解
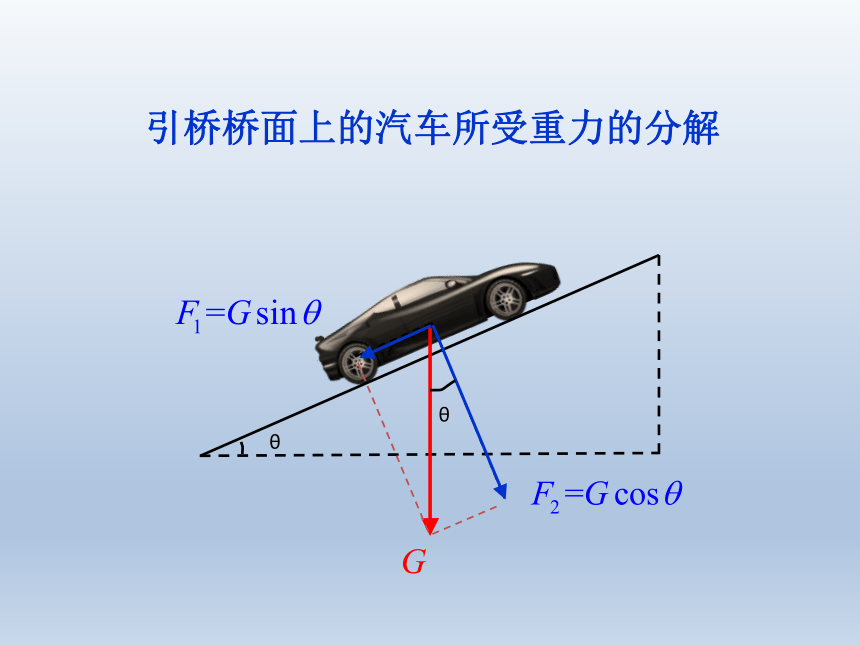
引桥桥面上的汽车所受重力的分解
θ
θ
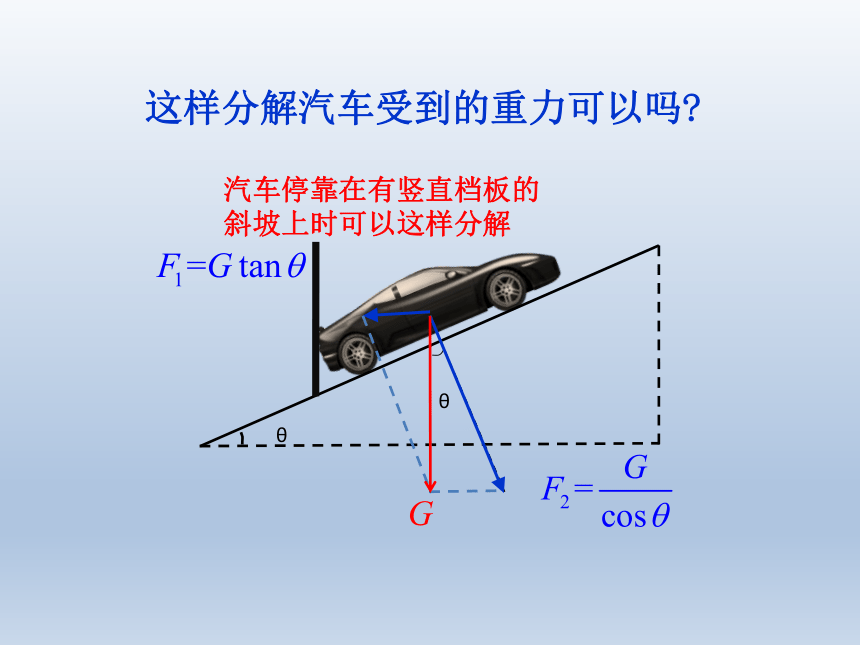
这样分解汽车受到的重力可以吗?
汽车停靠在有竖直档板的斜坡上时可以这样分解
θ
θ
F
G
G
G
F
a
b
F
探究:力的分解在实际生活中的运用
1、刀斧上的学问
2、三角支架的受力分析
G
G
G
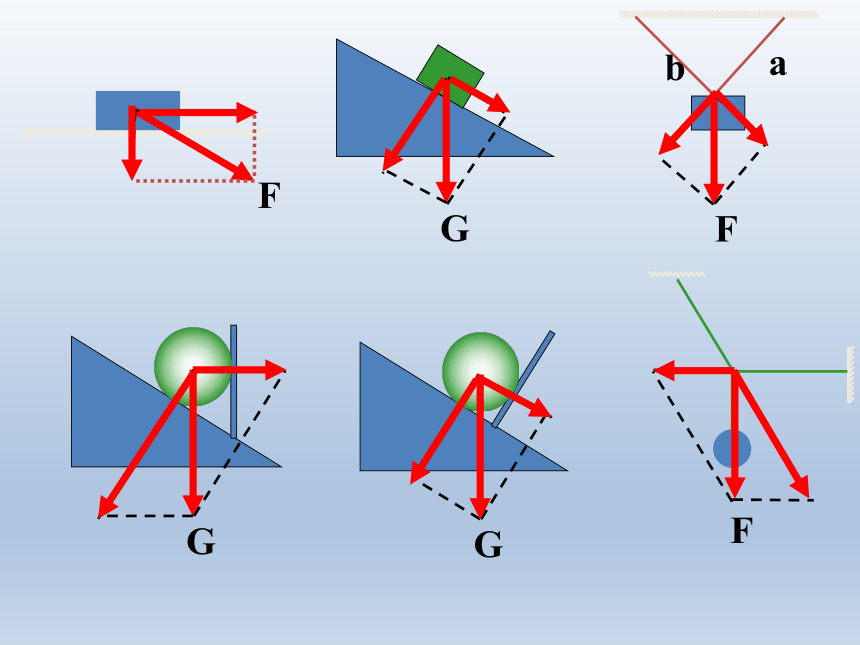
3、画出下图所示三种情况下重力的两个分力
F1
F2
F3
x
y
O
F2y
F1y
F1x
F3y
F3x
F2X
求三个力F1、F2与F3合力?
(1)正交分解
F
等效
方向:
将每一个力都分解到相互垂直的两个坐标轴上,然后分轴求合力,最后求总合力的大小和方向。
(2)正交分解法的操作步骤:
策略:欲合先分
例1
如图,物体重力为10N,AO绳与顶板间的夹角为45?,
BO绳水平,试用计算法求出AO绳和BO绳所受拉力的大小。
A
O
B
C
FOA
FOAX
FOAY
FOAY=FOAsin45?----②
FOAX=FOAcos45?----①
FOC=G
FOB
y
x
解:对O点受力分析如下图,分解FoA
有:
在X轴:FOAX==FOB------③
在Y轴:FOAY=FOC=G------④
∵O点静止,则有:
如图,氢气球被水平吹来的风吹成图示的情形,若测得
绳子与水平面的夹角为37?,已知气球受到空气的浮力为15N,
忽略氢气球的重力,求:
①氢气球受到的水平风力多大?
②绳子对氢气球的拉力多大?
风
37?
FTsin37 ? =F浮
FTcos37 ? =F风
FT
FTsin37
FTcos37
F风
例2
F浮=15N
y
x
o
α
如图,物体A的质量为m,斜面倾角α,A与斜面间的动摩擦因数为μ,斜面固定,现有一个水平力F作用在A上,当F多大时,物体A恰能沿斜面匀速向上运动?
F
FN=Fsinα+Gcosα
Fcosα=Gsinα+Ff
A
Gsinα
Gcosα
α
F
G
FN
Ff
Fsinα
Fcosα
Ff=μFN
例3
y
x
讨论:如果物体静止于斜面上,试分析摩擦力的方向和大小
(1)已知两分力的方向(唯一)
(2)已知一个分力的大小和方向(唯一)
(3)已知一个分力的大小和另一个分力的方向(不唯一)
三、力分解的情况
F1
F2
θ
F
F1
3.当F sinθ2.当F1 < Fsinθ 时
θ
F
4.当F1 > F 时
θ
F
1.当F1 = Fsinθ 时
θ
F
一组解
一组解
无解
两组解
F2
F2
F1
F1
F2
F11
F21
0
F12
F22
F13
F23
F24
F13
F25
F15
合力的大小和方向不变,分力F1的方向不变,F2的大小方向可变,当两分力的夹角变化时,方向不变的分力F1与夹角同变,方向可变的分力F2先减小(夹角为90度时最小)后增大。
怎样分解力
苏通长江公路大桥
斜拉桥的钢索对桥面产生的是怎样的作用?
大桥的引桥为什么要绕这么大的圈?
几个力
效果相同
一个力
分力
合力
力的分解
力的合成
一、力的分解
把已知力F作为平行四边形的对角线,与力F共点的平行四边形的两个邻边表示力F的两个分力。
2、法则:
1、定义:求一个已知力的分力
不加限制条件,一个力可分解为无数组不同的分力。
F
由一条对角线可以画出多少个平行四边形?
斜拉桥上一根钢索对桥面的作用力的分解
θ
O
F
F1
F2
F
按效果分解的一般步骤:
1、根据力F的作用效果,画出两个分力的方向;
2、把力F作为对角线,画出平行四边形,得出分力;
3、求解分力的大小和方向。
二、力的分解方法
按照效果分解
引桥桥面上的汽车所受重力的分解
θ
θ
这样分解汽车受到的重力可以吗?
汽车停靠在有竖直档板的斜坡上时可以这样分解
θ
θ
F
G
G
G
F
a
b
F
探究:力的分解在实际生活中的运用
1、刀斧上的学问
2、三角支架的受力分析
G
G
G
3、画出下图所示三种情况下重力的两个分力
F1
F2
F3
x
y
O
F2y
F1y
F1x
F3y
F3x
F2X
求三个力F1、F2与F3合力?
(1)正交分解
F
等效
方向:
将每一个力都分解到相互垂直的两个坐标轴上,然后分轴求合力,最后求总合力的大小和方向。
(2)正交分解法的操作步骤:
策略:欲合先分
例1
如图,物体重力为10N,AO绳与顶板间的夹角为45?,
BO绳水平,试用计算法求出AO绳和BO绳所受拉力的大小。
A
O
B
C
FOA
FOAX
FOAY
FOAY=FOAsin45?----②
FOAX=FOAcos45?----①
FOC=G
FOB
y
x
解:对O点受力分析如下图,分解FoA
有:
在X轴:FOAX==FOB------③
在Y轴:FOAY=FOC=G------④
∵O点静止,则有:
如图,氢气球被水平吹来的风吹成图示的情形,若测得
绳子与水平面的夹角为37?,已知气球受到空气的浮力为15N,
忽略氢气球的重力,求:
①氢气球受到的水平风力多大?
②绳子对氢气球的拉力多大?
风
37?
FTsin37 ? =F浮
FTcos37 ? =F风
FT
FTsin37
FTcos37
F风
例2
F浮=15N
y
x
o
α
如图,物体A的质量为m,斜面倾角α,A与斜面间的动摩擦因数为μ,斜面固定,现有一个水平力F作用在A上,当F多大时,物体A恰能沿斜面匀速向上运动?
F
FN=Fsinα+Gcosα
Fcosα=Gsinα+Ff
A
Gsinα
Gcosα
α
F
G
FN
Ff
Fsinα
Fcosα
Ff=μFN
例3
y
x
讨论:如果物体静止于斜面上,试分析摩擦力的方向和大小
(1)已知两分力的方向(唯一)
(2)已知一个分力的大小和方向(唯一)
(3)已知一个分力的大小和另一个分力的方向(不唯一)
三、力分解的情况
F1
F2
θ
F
F1
3.当F sinθ
θ
F
4.当F1 > F 时
θ
F
1.当F1 = Fsinθ 时
θ
F
一组解
一组解
无解
两组解
F2
F2
F1
F1
F2
F11
F21
0
F12
F22
F13
F23
F24
F13
F25
F15
合力的大小和方向不变,分力F1的方向不变,F2的大小方向可变,当两分力的夹角变化时,方向不变的分力F1与夹角同变,方向可变的分力F2先减小(夹角为90度时最小)后增大。
同课章节目录
- 开篇 激动人心的万千体验
- 01物理学——理性的追求
- 02物理学——人类文明的奇葩
- 03学物理——探究求真
- 第一章 怎样描述物体的运动
- 1 走近运动
- 2 怎样描述运动的快慢
- 3 怎样描述运动的快慢(续)
- 4 怎样描述速度变化的快慢
- 第二章 研究匀变速直线运动的规律
- 1 伽利略对落体运动的研究
- 2 自由落体运动的规律
- 3 匀变速直线运动的规律
- 4 匀变速直线运动规律的应用
- 第三章 力与相互作用
- 1 牛顿第三定律
- 2 弹力
- 3 摩擦力
- 4 分析物体的受力
- 第四章 怎样求合力与分力
- 1 怎样求合力
- 2 怎样分解力
- 3 共点力的平衡及其应用
- 第五章 研究力和运动的关系
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿运动定律的案例分析
- 5 超重与失重
