六年级下册数学课件 -《测量》 冀教版 (共18张PPT)
文档属性
| 名称 | 六年级下册数学课件 -《测量》 冀教版 (共18张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 06:41:04 | ||
图片预览



文档简介
(共18张PPT)
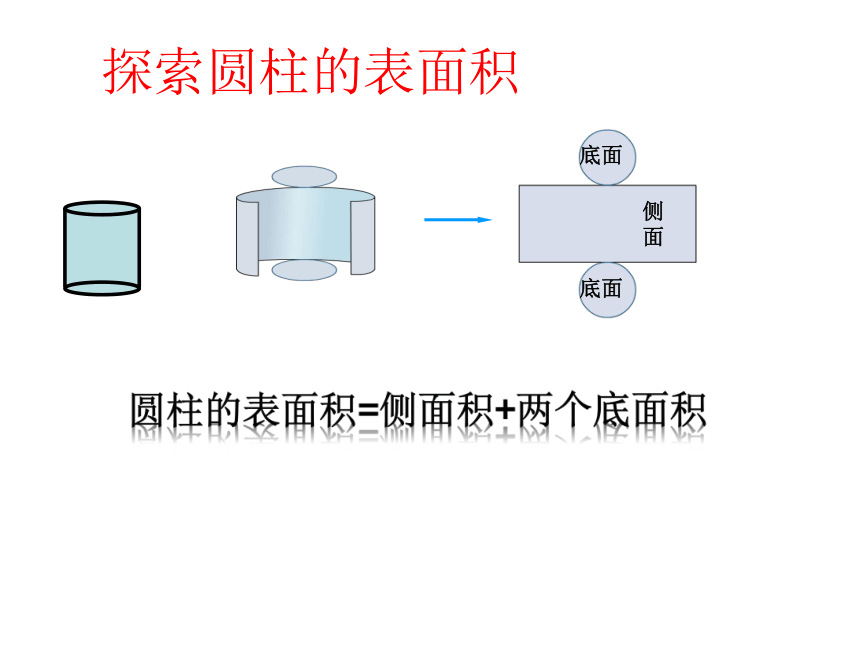
侧面
探索圆柱的表面积
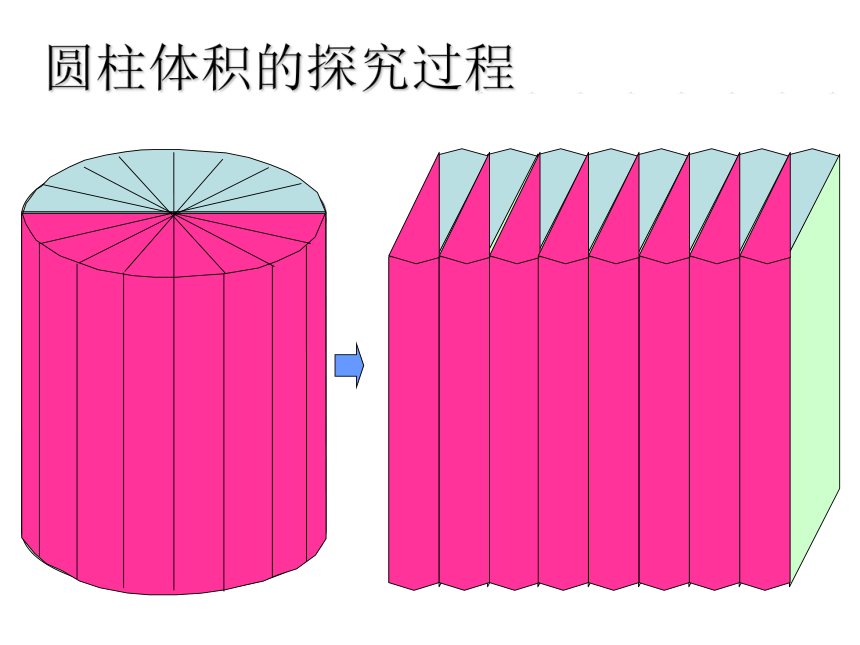
圆柱体积的探究过程
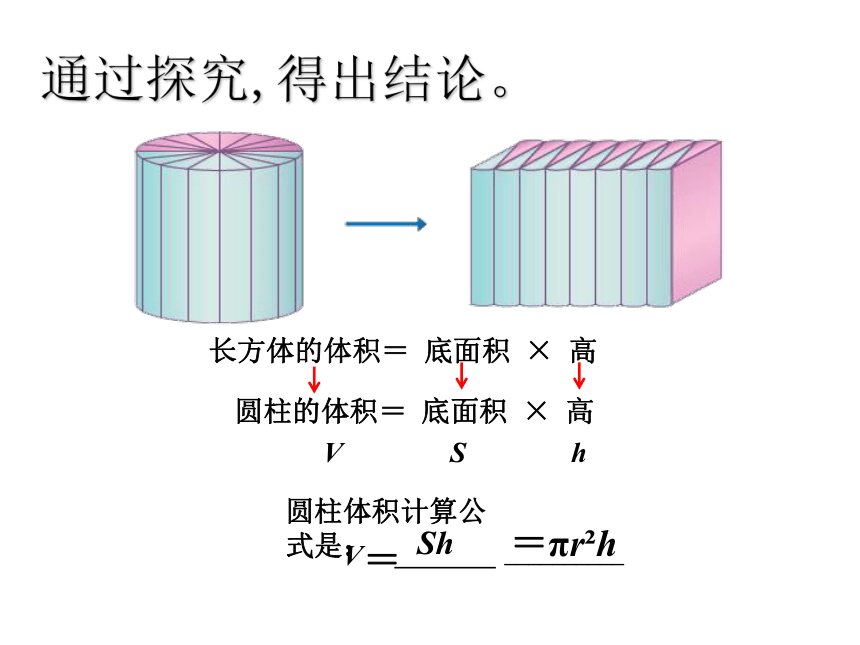
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
V
=
S
h
通过探究,得出结论。
=πr?h
Sh
__________
1、切割的方法
2、圆柱在采用不同方法切割之
后,它的形状、表面积和体积
各有什么变化呢?
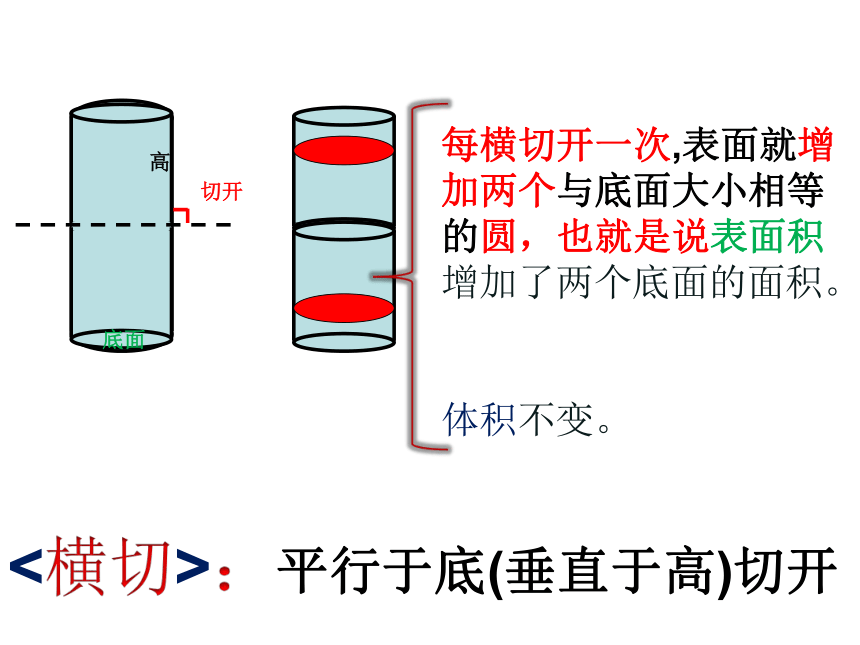
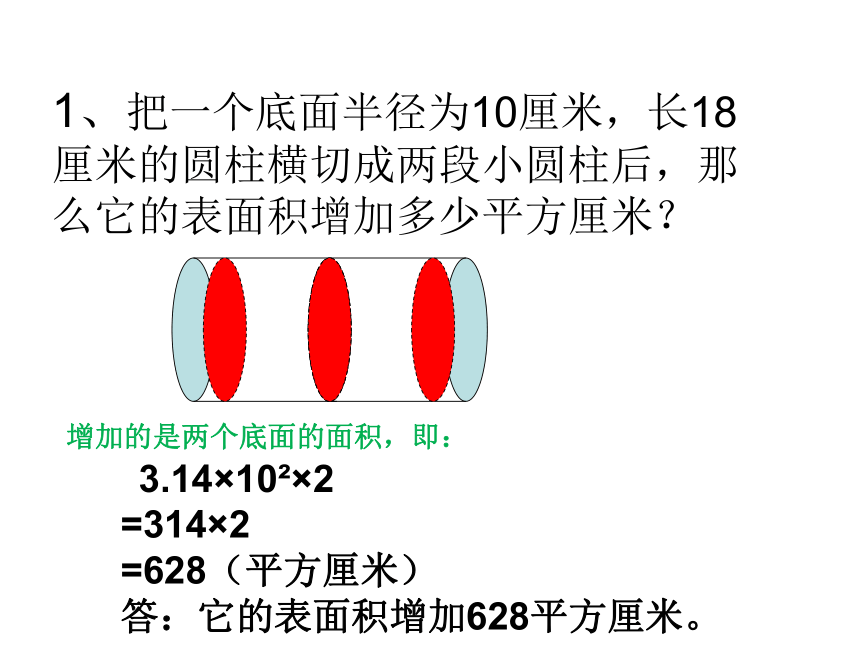
每横切开一次,表面就增加两个与底面大小相等的圆,也就是说表面积增加了两个底面的面积。
体积不变。
高
底面
1、把一个底面半径为10厘米,长18厘米的圆柱横切成两段小圆柱后,那么它的表面积增加多少平方厘米?
增加的是两个底面的面积,即:
3.14×10?×2
=314×2
=628(平方厘米)
答:它的表面积增加628平方厘米。
4
5
3
2.有一根圆柱形的木材,底面积是3平方分米,高为18分米,现在将它锯成 段,表面积增加了多少?
锯成两段,横切一次,表面积增加2个底面积。
锯成三段,横切两次,表面积增加4个底面积。
锯成四段,横切三次,表面积增加6个底面积。
锯成五段,横切四次,表面积增加8个底面积。
3-1=2(次)
2×2=4(个)
3×4=12(平方分米)
答:锯成三段,表面积增加了12平方分米。
5-1=4(次)
4×2=8(个)
3×8=24(平方分米)
答:锯成五段,表面积增加了24平方分米。
圆柱横切分段时,
增加的表面积的计算规律。
锯成n段,横切 ( ) 次,表面积增加( )个底面积。
n-1
(n-1)×2
锯成2段, 横切 1 次,表面积增加 2 个底面积。
锯成3段, 横切 2 次,表面积增加 4 个底面积。
锯成4段, 横切 3 次,表面积增加 6 个底面积。
锯成5段, 横切 4 次,表面积增加 8 个底面积。
表面积增加两个长方形的面积,
长方形的一边等于底面直径,另一边等于高。
体积不变。
<纵切>:圆柱沿底面直径和高切开
_________________
_________________
____________
____________
直径
高
纵切
一次
纵切1次,增加 2 个长方形(直径×高)的面积
纵切2次,增加( )个长方形( )的面积
纵切3次,增加( )个长方形( )的面积
纵切4次,增加( )个长方形( )的面积
纵切n次,增加( )个长方形( )的面积
4
6
8
2n
圆柱纵切时,
增加的表面积的计算规律。
直径×高
直径×高
直径×高
直径×高
一个圆柱,直径是2厘米。沿着直径纵切,表面积增加了20平方厘米。这个圆柱的体积是多少?
增加了两个长方形的面
宽(直径)
长(高)
20÷ 2=10(平方厘米)
10 ÷ 2=5(厘米)←
3.14×(2÷2)?×5=15.7(立方厘米)
答:这个圆柱的体积是15.7立方厘米。
一个长方形面的面积
高
------------------
斜切
4
4
3.14×(4÷2)?×(4+6)÷2
=3.14×2?×10÷2
=125.6÷2
=62.8(立方米)
这整个圆柱的体积除以2
4
6
6
4
求这块木料的体积。
单位(米)
答:这块木料的体积是62.8方米。
=
圆柱的切割
横切
纵切
斜切
共同点:表面积会增加,而体积不变。
1次,表面积增加两个圆(底面)的面积
1次,表面积增加两个长方形(直径×高)的面积
利用斜切之后体积不变做题
1、这节课你学会了什么?
2、关于切割你还想学习什么?
小结
谢谢!
侧面
探索圆柱的表面积
圆柱体积的探究过程
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
V
=
S
h
通过探究,得出结论。
=πr?h
Sh
__________
1、切割的方法
2、圆柱在采用不同方法切割之
后,它的形状、表面积和体积
各有什么变化呢?
每横切开一次,表面就增加两个与底面大小相等的圆,也就是说表面积增加了两个底面的面积。
体积不变。
高
底面
1、把一个底面半径为10厘米,长18厘米的圆柱横切成两段小圆柱后,那么它的表面积增加多少平方厘米?
增加的是两个底面的面积,即:
3.14×10?×2
=314×2
=628(平方厘米)
答:它的表面积增加628平方厘米。
4
5
3
2.有一根圆柱形的木材,底面积是3平方分米,高为18分米,现在将它锯成 段,表面积增加了多少?
锯成两段,横切一次,表面积增加2个底面积。
锯成三段,横切两次,表面积增加4个底面积。
锯成四段,横切三次,表面积增加6个底面积。
锯成五段,横切四次,表面积增加8个底面积。
3-1=2(次)
2×2=4(个)
3×4=12(平方分米)
答:锯成三段,表面积增加了12平方分米。
5-1=4(次)
4×2=8(个)
3×8=24(平方分米)
答:锯成五段,表面积增加了24平方分米。
圆柱横切分段时,
增加的表面积的计算规律。
锯成n段,横切 ( ) 次,表面积增加( )个底面积。
n-1
(n-1)×2
锯成2段, 横切 1 次,表面积增加 2 个底面积。
锯成3段, 横切 2 次,表面积增加 4 个底面积。
锯成4段, 横切 3 次,表面积增加 6 个底面积。
锯成5段, 横切 4 次,表面积增加 8 个底面积。
表面积增加两个长方形的面积,
长方形的一边等于底面直径,另一边等于高。
体积不变。
<纵切>:圆柱沿底面直径和高切开
_________________
_________________
____________
____________
直径
高
纵切
一次
纵切1次,增加 2 个长方形(直径×高)的面积
纵切2次,增加( )个长方形( )的面积
纵切3次,增加( )个长方形( )的面积
纵切4次,增加( )个长方形( )的面积
纵切n次,增加( )个长方形( )的面积
4
6
8
2n
圆柱纵切时,
增加的表面积的计算规律。
直径×高
直径×高
直径×高
直径×高
一个圆柱,直径是2厘米。沿着直径纵切,表面积增加了20平方厘米。这个圆柱的体积是多少?
增加了两个长方形的面
宽(直径)
长(高)
20÷ 2=10(平方厘米)
10 ÷ 2=5(厘米)←
3.14×(2÷2)?×5=15.7(立方厘米)
答:这个圆柱的体积是15.7立方厘米。
一个长方形面的面积
高
------------------
斜切
4
4
3.14×(4÷2)?×(4+6)÷2
=3.14×2?×10÷2
=125.6÷2
=62.8(立方米)
这整个圆柱的体积除以2
4
6
6
4
求这块木料的体积。
单位(米)
答:这块木料的体积是62.8方米。
=
圆柱的切割
横切
纵切
斜切
共同点:表面积会增加,而体积不变。
1次,表面积增加两个圆(底面)的面积
1次,表面积增加两个长方形(直径×高)的面积
利用斜切之后体积不变做题
1、这节课你学会了什么?
2、关于切割你还想学习什么?
小结
谢谢!
