人教版八年级数学上册14.3 因式分解14.3.2 公式法(完全平方公式)课件(共66张 含动画)
文档属性
| 名称 | 人教版八年级数学上册14.3 因式分解14.3.2 公式法(完全平方公式)课件(共66张 含动画) |  | |
| 格式 | zip | ||
| 文件大小 | 11.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 20:07:31 | ||
图片预览







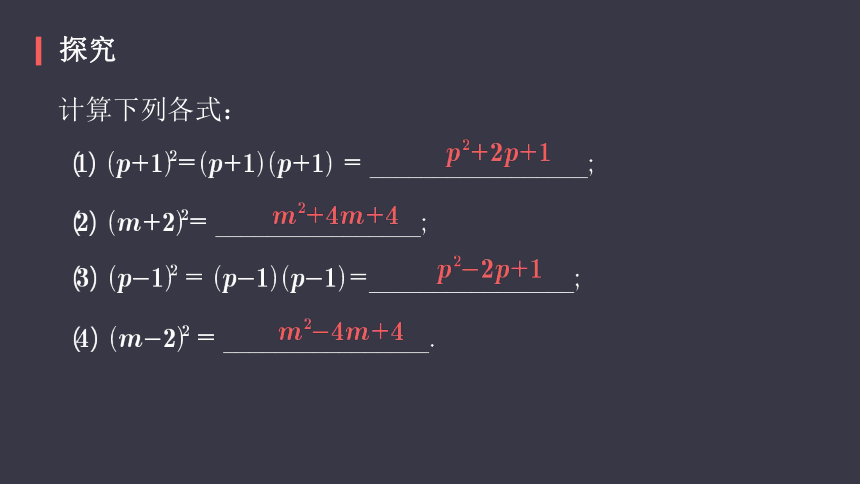

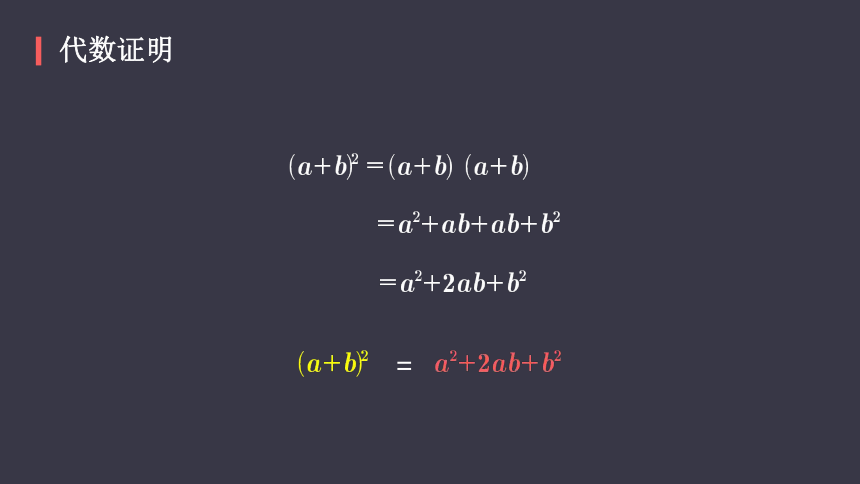

文档简介
(共66张PPT)
完全平方公式
教学目标
理解完全平方公式,能用公式进行计算.
经历探索完全平方公式的过程,进而感受特殊到一般、数形结合思想,发展符号意识和几何直观观念.?
教学重点
完全平方公式的推导和运用.
教学难点
理解完全平方公式的结构特征,灵活应用完全平方公式.
知识回顾
多项式乘多项式的法则
(a + b)(p + q)=?
ap
+ aq
+ bp
+ bq
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
一位老人非常喜欢孩子.
每当有孩子到他家做客时,老人都要拿出糖果招待他们.来一个孩子,老人就给这个孩子一块糖,
来两个孩子,老人就给每个孩子两块塘,
……
(1)第一天有a个男孩去了老人家,老人一共给了这些孩子多少块糖?
(2)第二天有b个女孩去了老人家,老人一共给了这些孩子多少块糖?
一位老人非常喜欢孩子.
每当有孩子到他家做客时,老人都要拿出糖果招待他们.来一个孩子,老人就给这个孩子一块糖,
来两个孩子,老人就给每个孩子两块塘,
……
(3)第三天这(a+b)个孩子一起去看老人,老人一共给了这些孩子多少块糖?
(4)这些孩子第三天得到的糖果数与前两天他们得到的糖果总数哪个多?多多少?
这个式子有什么特点?
这是两个数的平方和
你知道怎么算这种式子吗?
下面就来探究一下.
探究
计算下列各式:
完全平方和
观察式子,回答下列问问题:
①等式左边都是两个数_____________
②等式右边都是两个数_____________,再加上这两个数_____________
你能用一个式子概括上述规律吗?
和的平方
平方的和
积的两倍
=
怎么证明呢?
代数证明
=
几何证明
ab
ab
=
完全平方差
观察式子,回答下列问问题:
①等式左边都是两个数_____________
②等式右边都是两个数_____________,再减去这两个数_____________
你能用一个式子概括上述规律吗?
差的平方
平方的和
积的两倍
=
怎么证明呢?
代数证明
=
几何证明
=
=
完全平方公式
=
=
你能用文字语言表述完全平方公式吗?
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
公式特点
=
=
①积为_______次_______项式.
②积中两项为两数的平方_____,另一项为两数的____的_______,且符号与等式左边符号________.
③公式中的字母a,b可以单个的数或字母,也可以表示式子.
二
三
和
积
2倍
相同
巧记口诀
=
=
首平方
尾平方
2倍乘积放中央
2倍符号看前方
怎么推导完全平方公式?
利用完全平方公式计算应该注意什么?
完全平方公式
易错点
下面各式的计算是否正确?如果不正确,说明错的原因?
漏了中间项
漏了中间项,且符号错误
中间项符号不对
漏了中间项的系数2
例题
运用完全平方公式计算:
a
a
b
b
解:
例题
运用完全平方公式计算:
方法一:
方法二:
哪种方法比较简单?
总结:为了简便,可以先把括号内变形为首项为正的.
思考
练习
1.运用完全平方公式计算:
练习
2.下面各式的计算错在哪里?应当怎么改正?
漏了中间项
漏了中间项的系数2
练习
运用完全平方公式计算:
练习
运用完全平方公式计算:
练习
运用完全平方公式计算:
练习
运用完全平方公式计算:
补充题
答案:3
例题
运用完全平方公式计算:
练习
练习
运用完全平方公式计算:
练习
运用完全平方公式计算:
添括号法则
之前我们学习过去括号法则
反过来,可以得到添括号法则
归纳
添括号时,
括号前是正号时,括到括号里的各项都不变符号;
如果括号前面是负号,括到括号里的各项都改变符号.
在等式右边的括号内填上适当的项:
点睛:“-”变,“+”不变,要变全都变
思考:怎么检验添括号是否正确呢?
从右往左去括号
练习
判断下列运算是否正确,不正确的请改正:
例题
运用乘法公式计算:
(1)(x+2y-3)(x-2y+3)
这个符合完全平方公式还是平方差公式?
有两个括号,只能是平方差公式
先变形
原式=[x+(2y-3)][x-( 2y-3)]
再化简
例题
运用乘法公式计算:
这个符合完全平方公式还是平方差公式?
只有一个括号,只能是完全平方公式
先变形
再化简
归纳
1.如何判断应该选择哪个公式?
2.括号内有三项时怎么利用公式?
根据式子中括号的个数,一个括号,就用_________________,两个括号,就用_________________ .
添括号,把三项变成两项.
完全平方公式
平方差公式
练习
1.在等号右边的括号内填上适当的项,并用去括号法则检验.
(1)a+b-c=a+( ? ? ? ? ?)
(2)a-b-c=a-( ? ? ? ? ?)
(3)a+b-c=a-( ? ? ? ? ?)
(4)a+b+c=a-( ? ? ? ? ?)
练习
2.运用乘法公式计算:
(2)(2x+y+z)(2x-y-z)
练习
已知x,y的和与差的平方求积
已知x,y的和与差的平方求积
答案:8
已知x,y的和与积求平方和
答案:7
已知x,y的和与积求平方和
答案:69
已知x,y的和与积求平方和
答案:11或-11
已知x,y的和与积,如何求x,y的平方和.
已知x、y的积与和求代数式的值
完全平方公式的几何意义
总结
这节课我们学会了什么?
=
=
首平方
尾平方
2倍乘积放中央
2倍符号看前方
总结
这节课我们还学会了什么?
1.如何判断应该选择哪个公式?
2.括号内有三项时怎么利用公式?
根据式子中括号的个数,一个括号,就用_________________,两个括号,就用_________________ .
添括号,把三项变成两项.
完全平方公式
平方差公式
复习巩固
1.运用平方差公式计算:
复习巩固
2.运用完全平方公式计算:
综合运用
3.运用乘法公式计算:
综合运用
4.先化简,再求值:
综合运用
综合运用
6.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积.
拓广探索
拓广探索
拓广探索
9.解方程组
杨辉三角
我国著名数学家华罗庚曾在给青少年撰写的“数学是我国人民所擅长的学科”一文中谈到,我国古代数学的许多创新与发展都曾居世界前列.他说:“实际上我们祖国伟大人民在人类史上,有过无比睿智的成就.”其中”杨辉三角“(图1)就是一例.
在我国南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用图1的三角形解释二项和的乘方规律.杨辉在注释中提到,在他之前北宋数学家贾宪(1050年左右)也用过上述方法,因此我们称这个三角形为”杨辉三角“或”贾宪三角“.
杨辉三角
这个三角形被欧洲学者称为“帕斯卡三角”.法国数学家帕斯卡(Pascal,1623-1662)于1654年发现了此三角形.
杨辉三角
完全平方公式
教学目标
理解完全平方公式,能用公式进行计算.
经历探索完全平方公式的过程,进而感受特殊到一般、数形结合思想,发展符号意识和几何直观观念.?
教学重点
完全平方公式的推导和运用.
教学难点
理解完全平方公式的结构特征,灵活应用完全平方公式.
知识回顾
多项式乘多项式的法则
(a + b)(p + q)=?
ap
+ aq
+ bp
+ bq
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
一位老人非常喜欢孩子.
每当有孩子到他家做客时,老人都要拿出糖果招待他们.来一个孩子,老人就给这个孩子一块糖,
来两个孩子,老人就给每个孩子两块塘,
……
(1)第一天有a个男孩去了老人家,老人一共给了这些孩子多少块糖?
(2)第二天有b个女孩去了老人家,老人一共给了这些孩子多少块糖?
一位老人非常喜欢孩子.
每当有孩子到他家做客时,老人都要拿出糖果招待他们.来一个孩子,老人就给这个孩子一块糖,
来两个孩子,老人就给每个孩子两块塘,
……
(3)第三天这(a+b)个孩子一起去看老人,老人一共给了这些孩子多少块糖?
(4)这些孩子第三天得到的糖果数与前两天他们得到的糖果总数哪个多?多多少?
这个式子有什么特点?
这是两个数的平方和
你知道怎么算这种式子吗?
下面就来探究一下.
探究
计算下列各式:
完全平方和
观察式子,回答下列问问题:
①等式左边都是两个数_____________
②等式右边都是两个数_____________,再加上这两个数_____________
你能用一个式子概括上述规律吗?
和的平方
平方的和
积的两倍
=
怎么证明呢?
代数证明
=
几何证明
ab
ab
=
完全平方差
观察式子,回答下列问问题:
①等式左边都是两个数_____________
②等式右边都是两个数_____________,再减去这两个数_____________
你能用一个式子概括上述规律吗?
差的平方
平方的和
积的两倍
=
怎么证明呢?
代数证明
=
几何证明
=
=
完全平方公式
=
=
你能用文字语言表述完全平方公式吗?
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
公式特点
=
=
①积为_______次_______项式.
②积中两项为两数的平方_____,另一项为两数的____的_______,且符号与等式左边符号________.
③公式中的字母a,b可以单个的数或字母,也可以表示式子.
二
三
和
积
2倍
相同
巧记口诀
=
=
首平方
尾平方
2倍乘积放中央
2倍符号看前方
怎么推导完全平方公式?
利用完全平方公式计算应该注意什么?
完全平方公式
易错点
下面各式的计算是否正确?如果不正确,说明错的原因?
漏了中间项
漏了中间项,且符号错误
中间项符号不对
漏了中间项的系数2
例题
运用完全平方公式计算:
a
a
b
b
解:
例题
运用完全平方公式计算:
方法一:
方法二:
哪种方法比较简单?
总结:为了简便,可以先把括号内变形为首项为正的.
思考
练习
1.运用完全平方公式计算:
练习
2.下面各式的计算错在哪里?应当怎么改正?
漏了中间项
漏了中间项的系数2
练习
运用完全平方公式计算:
练习
运用完全平方公式计算:
练习
运用完全平方公式计算:
练习
运用完全平方公式计算:
补充题
答案:3
例题
运用完全平方公式计算:
练习
练习
运用完全平方公式计算:
练习
运用完全平方公式计算:
添括号法则
之前我们学习过去括号法则
反过来,可以得到添括号法则
归纳
添括号时,
括号前是正号时,括到括号里的各项都不变符号;
如果括号前面是负号,括到括号里的各项都改变符号.
在等式右边的括号内填上适当的项:
点睛:“-”变,“+”不变,要变全都变
思考:怎么检验添括号是否正确呢?
从右往左去括号
练习
判断下列运算是否正确,不正确的请改正:
例题
运用乘法公式计算:
(1)(x+2y-3)(x-2y+3)
这个符合完全平方公式还是平方差公式?
有两个括号,只能是平方差公式
先变形
原式=[x+(2y-3)][x-( 2y-3)]
再化简
例题
运用乘法公式计算:
这个符合完全平方公式还是平方差公式?
只有一个括号,只能是完全平方公式
先变形
再化简
归纳
1.如何判断应该选择哪个公式?
2.括号内有三项时怎么利用公式?
根据式子中括号的个数,一个括号,就用_________________,两个括号,就用_________________ .
添括号,把三项变成两项.
完全平方公式
平方差公式
练习
1.在等号右边的括号内填上适当的项,并用去括号法则检验.
(1)a+b-c=a+( ? ? ? ? ?)
(2)a-b-c=a-( ? ? ? ? ?)
(3)a+b-c=a-( ? ? ? ? ?)
(4)a+b+c=a-( ? ? ? ? ?)
练习
2.运用乘法公式计算:
(2)(2x+y+z)(2x-y-z)
练习
已知x,y的和与差的平方求积
已知x,y的和与差的平方求积
答案:8
已知x,y的和与积求平方和
答案:7
已知x,y的和与积求平方和
答案:69
已知x,y的和与积求平方和
答案:11或-11
已知x,y的和与积,如何求x,y的平方和.
已知x、y的积与和求代数式的值
完全平方公式的几何意义
总结
这节课我们学会了什么?
=
=
首平方
尾平方
2倍乘积放中央
2倍符号看前方
总结
这节课我们还学会了什么?
1.如何判断应该选择哪个公式?
2.括号内有三项时怎么利用公式?
根据式子中括号的个数,一个括号,就用_________________,两个括号,就用_________________ .
添括号,把三项变成两项.
完全平方公式
平方差公式
复习巩固
1.运用平方差公式计算:
复习巩固
2.运用完全平方公式计算:
综合运用
3.运用乘法公式计算:
综合运用
4.先化简,再求值:
综合运用
综合运用
6.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积.
拓广探索
拓广探索
拓广探索
9.解方程组
杨辉三角
我国著名数学家华罗庚曾在给青少年撰写的“数学是我国人民所擅长的学科”一文中谈到,我国古代数学的许多创新与发展都曾居世界前列.他说:“实际上我们祖国伟大人民在人类史上,有过无比睿智的成就.”其中”杨辉三角“(图1)就是一例.
在我国南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用图1的三角形解释二项和的乘方规律.杨辉在注释中提到,在他之前北宋数学家贾宪(1050年左右)也用过上述方法,因此我们称这个三角形为”杨辉三角“或”贾宪三角“.
杨辉三角
这个三角形被欧洲学者称为“帕斯卡三角”.法国数学家帕斯卡(Pascal,1623-1662)于1654年发现了此三角形.
杨辉三角
