人教版八年级数学上册14.3 因式分解14.3.2 公式法(平方差公式)课件(共42张 含动画)
文档属性
| 名称 | 人教版八年级数学上册14.3 因式分解14.3.2 公式法(平方差公式)课件(共42张 含动画) |  | |
| 格式 | zip | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 20:00:15 | ||
图片预览











文档简介
(共42张PPT)
公式法之平方差公式
探索并运用平方差公式进行因式分解,体会转化思想.??
会综合运用提公因式法和平方差公式对多项式进
行因式分解.
教学目标
运用平方差公式来分解因式
教学重点
教学难点
灵活运用平方差公式分解因式
知识回顾
1.什么是因式分解?
把一个多项式化成几个整式积的形式,
这种变形叫做把这个多项式因式分解,
也叫把这个多项式分解因式.
2.因式分解和整式乘法有什么关系?
(x-1)(x+1)
因式分解与整式乘法是方向相反的变形
知识回顾
判断下列各式哪些是因式分解?哪些不是.
知识回顾
把下列各式进行因式分解:
回顾平方差公式
在横线内填上适当的式子,使等式成立:
这个过程是整式乘法
这个过程是因式分解
思考
你能将多项式
分解因式吗?
已知
所以
整式乘法
因式分解
因式分解的平方差公式
两个数的平方差,等于这两个数的和与这两个数的差的积.
公式法
逆用乘法公式将一个多项式因式分解的方法叫做公式法.
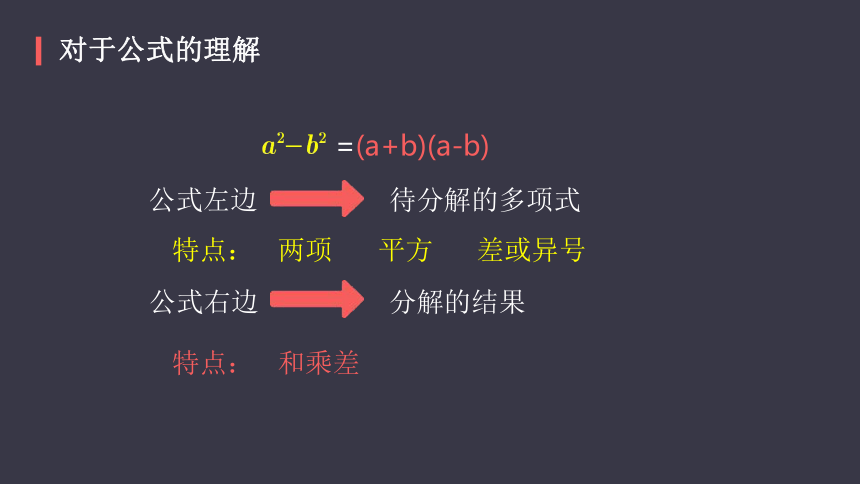
对于公式的理解
=(a+b)(a-b)
公式左边
待分解的多项式
特点:
两项
平方
差或异号
公式右边
分解的结果
特点:
和乘差
是否满足平方差
下列各式能否用平方差公式分解?如果能分解,分解成什么?如不能说明理由.
不能
不能
平方差的形式
下列多项式能转化成? ? ? ? ? ? ? ? ? ? 的形式吗?
如果能,请将其转化成? ? ? ? ? ? ? ? ? ? 的形式.
不能转化为平方差形式
不能转化为平方差形式
知识铺垫
知识铺垫
填空:
总结:先化成平方差的形式,再分解
平方差公式中的“a”和“b”可以表示单项式,也可以表示多项式.
分解因式
分解下列因式:
分解下列因式:
分解下列因式:
分解下列因式:
分解下列因式:
分解下列因式:
分解完了吗?
这能直接用平方差公式吗?
得先提取公因式
因式分解注意事项:?
1.能提一定要先提;
2.分解一定要彻底.
分解因式:
分解因式:
分解因式:
分解因式:
分解因式:
易错点
判断下列因式分解是否正确
分析
答案
易错点
判断下列因式分解是否正确.
答案
分析
仍需继续分解
1.下列多项式能否用平方差公式分解因式?为什么?
2.分解因式:
利用平方差公式计算
利用因式分解计算:
利用平方差公式计算
利用平方差公式计算
利用平方差公式计算
利用因式分解计算:
解:原式=(100+99)(100-99)+(98+97)(98-97) +… +(2+1)(2-1)
=100+99+98+97 +… +2+1
=5050
利用平方差公式计算
整除问题
整除问题
整除问题
平方差公式的实际应用
如图,在边长为6.8cm正方形钢板上,挖去4个边长为1.6cm的小正方形,求剩余部分的面积.
平方差公式的实际应用
总结
这节课我们学会了什么?
1.因式分解的平方差公式:
2.用平方差公式分解因式的步骤:
先化成平方差的形式,再分解
3.因式分解的注意事项:
①能提一定要先提;②分解一定要彻底.
利用平方差公式分解因式时应该注意什么?
如何利用平方差公式分解因式?
公式法之平方差公式
公式法之平方差公式
探索并运用平方差公式进行因式分解,体会转化思想.??
会综合运用提公因式法和平方差公式对多项式进
行因式分解.
教学目标
运用平方差公式来分解因式
教学重点
教学难点
灵活运用平方差公式分解因式
知识回顾
1.什么是因式分解?
把一个多项式化成几个整式积的形式,
这种变形叫做把这个多项式因式分解,
也叫把这个多项式分解因式.
2.因式分解和整式乘法有什么关系?
(x-1)(x+1)
因式分解与整式乘法是方向相反的变形
知识回顾
判断下列各式哪些是因式分解?哪些不是.
知识回顾
把下列各式进行因式分解:
回顾平方差公式
在横线内填上适当的式子,使等式成立:
这个过程是整式乘法
这个过程是因式分解
思考
你能将多项式
分解因式吗?
已知
所以
整式乘法
因式分解
因式分解的平方差公式
两个数的平方差,等于这两个数的和与这两个数的差的积.
公式法
逆用乘法公式将一个多项式因式分解的方法叫做公式法.
对于公式的理解
=(a+b)(a-b)
公式左边
待分解的多项式
特点:
两项
平方
差或异号
公式右边
分解的结果
特点:
和乘差
是否满足平方差
下列各式能否用平方差公式分解?如果能分解,分解成什么?如不能说明理由.
不能
不能
平方差的形式
下列多项式能转化成? ? ? ? ? ? ? ? ? ? 的形式吗?
如果能,请将其转化成? ? ? ? ? ? ? ? ? ? 的形式.
不能转化为平方差形式
不能转化为平方差形式
知识铺垫
知识铺垫
填空:
总结:先化成平方差的形式,再分解
平方差公式中的“a”和“b”可以表示单项式,也可以表示多项式.
分解因式
分解下列因式:
分解下列因式:
分解下列因式:
分解下列因式:
分解下列因式:
分解下列因式:
分解完了吗?
这能直接用平方差公式吗?
得先提取公因式
因式分解注意事项:?
1.能提一定要先提;
2.分解一定要彻底.
分解因式:
分解因式:
分解因式:
分解因式:
分解因式:
易错点
判断下列因式分解是否正确
分析
答案
易错点
判断下列因式分解是否正确.
答案
分析
仍需继续分解
1.下列多项式能否用平方差公式分解因式?为什么?
2.分解因式:
利用平方差公式计算
利用因式分解计算:
利用平方差公式计算
利用平方差公式计算
利用平方差公式计算
利用因式分解计算:
解:原式=(100+99)(100-99)+(98+97)(98-97) +… +(2+1)(2-1)
=100+99+98+97 +… +2+1
=5050
利用平方差公式计算
整除问题
整除问题
整除问题
平方差公式的实际应用
如图,在边长为6.8cm正方形钢板上,挖去4个边长为1.6cm的小正方形,求剩余部分的面积.
平方差公式的实际应用
总结
这节课我们学会了什么?
1.因式分解的平方差公式:
2.用平方差公式分解因式的步骤:
先化成平方差的形式,再分解
3.因式分解的注意事项:
①能提一定要先提;②分解一定要彻底.
利用平方差公式分解因式时应该注意什么?
如何利用平方差公式分解因式?
公式法之平方差公式
