人教新课标A版必修4第一章课件:1.5函数y=Asin(ωx φ)的图象 课件(共35张PPT)
文档属性
| 名称 | 人教新课标A版必修4第一章课件:1.5函数y=Asin(ωx φ)的图象 课件(共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-12 17:34:32 | ||
图片预览







文档简介
(共35张PPT)
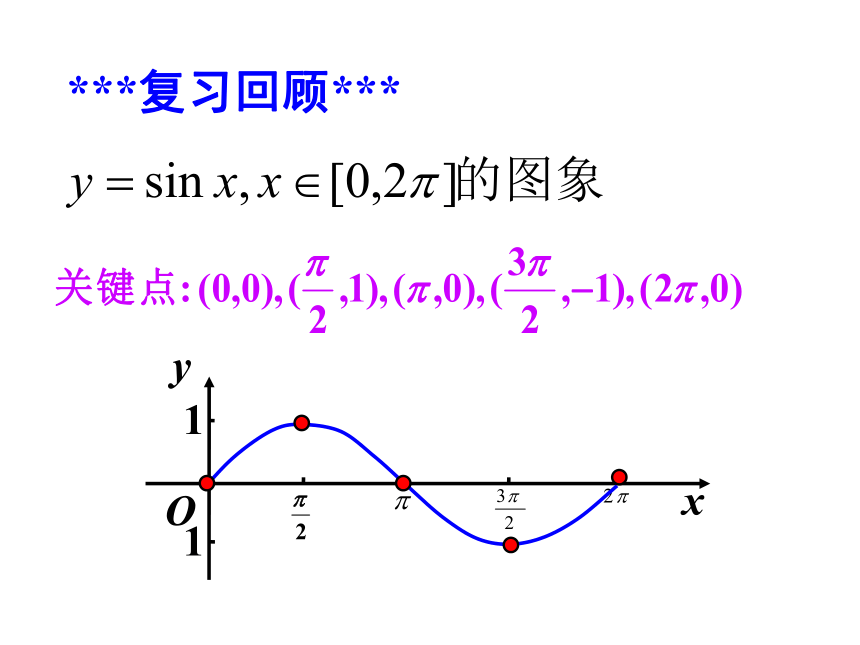
***复习回顾***
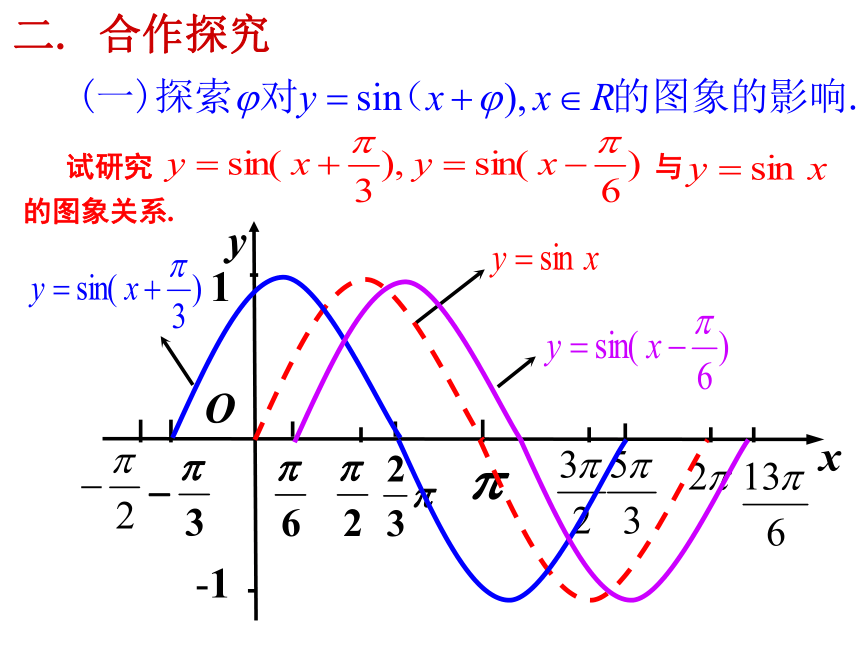
试研究 与 的图象关系.
二. 合作探究
1
-1
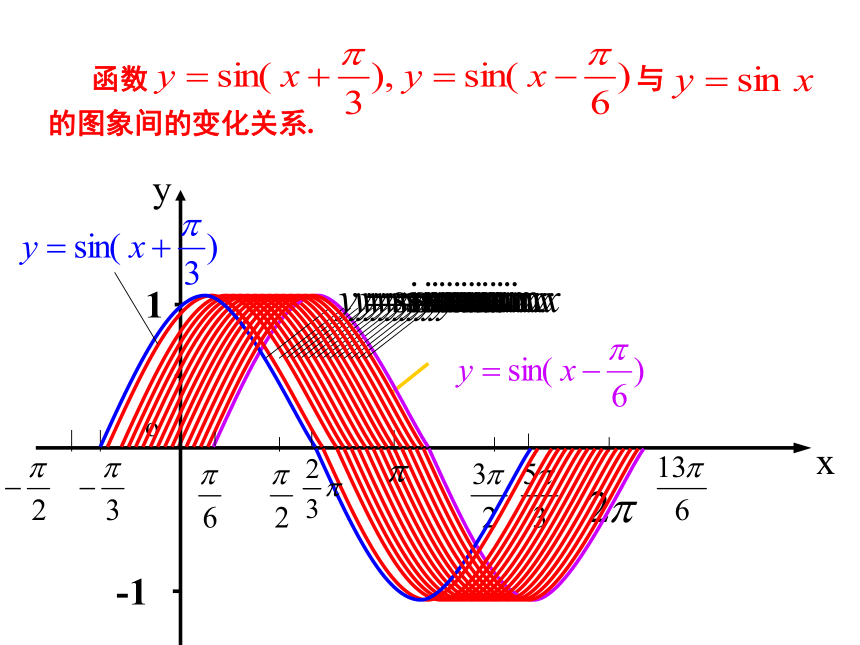
函数 与 的图象间的变化关系.
所有的点向左(? >0)
或向右(? <0)平移
| ? | 个单位
函数y=sin(x+?)图象:
函数 y=sin(x+?)(??0) 的图象可以看作是把y=sinx 的图象上所有的点向左(当?>0时)或向右(当?<0时)平行移动|?|个单位而得到的.
y=sinx
y=sin(x+?)
?的变化引起图象位置发生变化(左加右减)
平移变换
总结
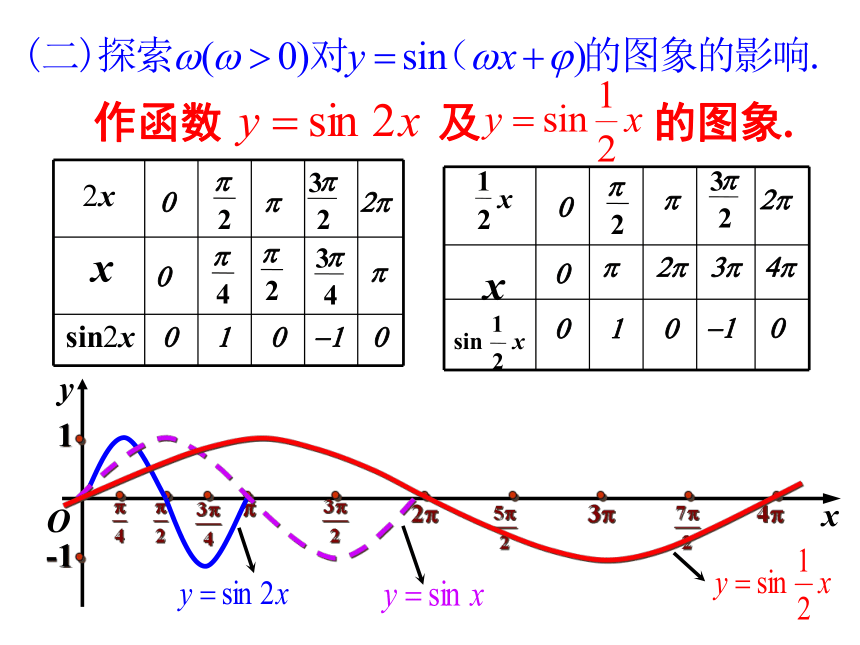
作函数 及 的图象.
所有的点横坐标缩短(?>1)或伸长(0< ?<1) 1/?倍
函数y=sin?x(?>0)图象:
函数 y=sin?x (?>0且??0) 的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当?>1时)或伸长(当0< ?<1时)到原来的1/?倍(纵坐标不变)而得到的.
周期变换
y=sinx
y=sin?x
纵坐标不变
?决定函数的周期:
总结
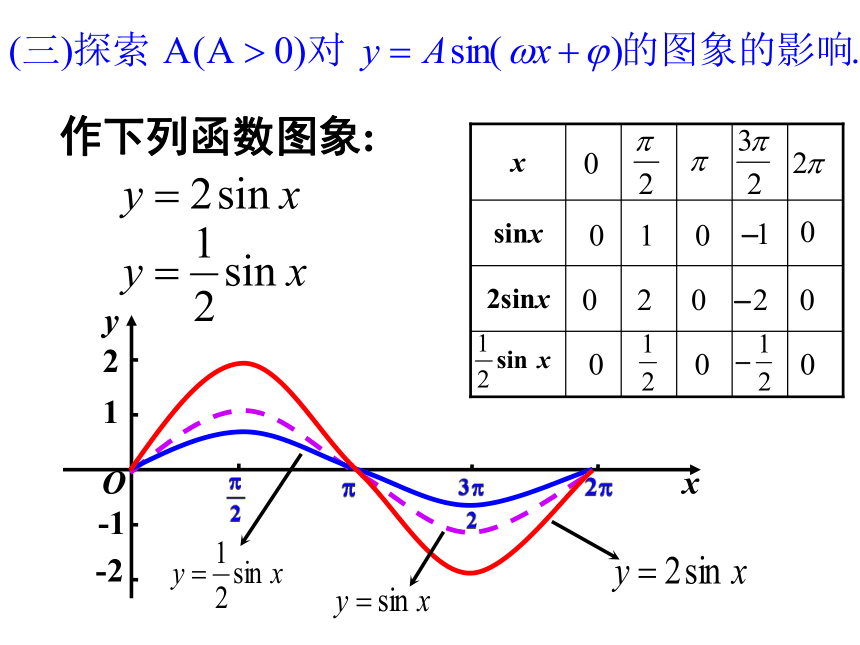
作下列函数图象:
振幅变换
y=sinx
y=Asinx
所有的点纵坐标伸长(A>1)或缩短(0< A<1) A倍
横坐标不变
函数y=Asinx(A>0)图象:
函数 y=Asinx(A>0且A?1) 的图象可以看作是把y=sinx的图象上所有点的纵坐标伸长(当A>1时)或缩短(当0< A<1时)到原来的A倍(横坐标不变)而得到的.
A的大小决定这个函数的最大(小)值
y=Asinx,x?R的值域是[-A, A],
最大值是A,最小值是-A.
总结
方法1:
方法1:(按 先平移后变周期的顺序变换)
y=sinx
y=sin(x+?)
横坐标缩短?>1 (伸长0y=sin(?x+?)
纵坐标伸长A>1 (缩短0y=Asin(?x+?)
y=sinx
y=Asin(?x+?)
总结:
向左?>0 (向右?<0)
方法1:按先平移后变周期的顺序变换
平移|?|个单位
纵坐标不变
横坐标不变
步骤1
步骤2
步骤3
步骤4
步骤5
沿x轴 平行移动
横坐标 伸长或缩短
纵坐标 伸长或缩短
沿x轴 扩展
2?
?
方法2:
方法2:(按先变周期后平移顺序变换)
y=sinx
横坐标缩短?>1 (伸长0y=sin?x
纵坐标伸长A>1 (缩短0y=Asin(?x+?)
y=sinx
y=Asin(?x+?)
总结:
纵坐标不变
横坐标不变
方法2:按先变周期后平移顺序变换
向左?>0 (向右?<0)
平移|?|/?个单位
物理中
例2:右图是某简谐运动的图象。
(1)这个简谐运动
的振幅、周期与
频率各是多少?
(2)从O点算起,到曲线上的哪一点,表示完成了一次往复运动?如从A点算起呢?
(3)求这个简谐运动的函数表达式.
例3:已知函数y=Asin(?x+?)(?>0, A>0)
的图像如下:
求解析式?
练习:如图,某地一天从6~14时的温度变化曲线近似满足函数:
这段曲线对应的函数是什么?
总结:求函数 的方法。
“第一点”为:
“第二点”为:
“第三点”为:
“第四点”为:
“第五点”为:
1. 要得到函数 y= 2 sin x 的图象,只需将 y= sinx 图象( )
A.横坐标扩大原来的两倍 B. 纵坐标扩大原来的两倍
C.横坐标扩大到原来的两倍 D. 纵坐标扩大到原来的两倍
2. 要得到函数 y=sin3x 的图象,只需将 y=sinx 图象( )
A. 横坐标扩大原来的3倍 B.横坐标扩大到原来的3倍
C. 横坐标缩小原来的1/3倍 D.横坐标缩小到原来的1/3倍
3. 要得到函数 y=sin(x + π/3)的图象,只需将 y=sinx 图象( )
A. 向左平移π/6个单位 B. 向右平移π/6个单位
C. 向左平移π/3个单位 D. 向右平移π/3个单位
4. 要得到函数 y=sin(2x-π/3)的图象,只需将y=sin2x图象( )
A. 向左平移π/3 个单位 B. 向右平移π/3个单位
C. 向左平移π/ 6个单位 D. 向右平移π/6 个单位
D
D
C
D
练习
C
B
C
D
C
A
关键:
小结
所有的点向左(? >0)
或向右(? <0)平行移动
| ? | 个单位长度
y=sinx
y=sin(x+?)
y=sinx
y=sin?x
横坐标缩短(?>1)或
伸长(0< ?<1) 1/?倍
纵坐标不变
y=sinx
y=Asinx
纵坐标伸长(A>1)或
缩短(0< A<1) A倍
横坐标不变
y=Asin(?x+ ?)
y=sinx
***复习回顾***
试研究 与 的图象关系.
二. 合作探究
1
-1
函数 与 的图象间的变化关系.
所有的点向左(? >0)
或向右(? <0)平移
| ? | 个单位
函数y=sin(x+?)图象:
函数 y=sin(x+?)(??0) 的图象可以看作是把y=sinx 的图象上所有的点向左(当?>0时)或向右(当?<0时)平行移动|?|个单位而得到的.
y=sinx
y=sin(x+?)
?的变化引起图象位置发生变化(左加右减)
平移变换
总结
作函数 及 的图象.
所有的点横坐标缩短(?>1)或伸长(0< ?<1) 1/?倍
函数y=sin?x(?>0)图象:
函数 y=sin?x (?>0且??0) 的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当?>1时)或伸长(当0< ?<1时)到原来的1/?倍(纵坐标不变)而得到的.
周期变换
y=sinx
y=sin?x
纵坐标不变
?决定函数的周期:
总结
作下列函数图象:
振幅变换
y=sinx
y=Asinx
所有的点纵坐标伸长(A>1)或缩短(0< A<1) A倍
横坐标不变
函数y=Asinx(A>0)图象:
函数 y=Asinx(A>0且A?1) 的图象可以看作是把y=sinx的图象上所有点的纵坐标伸长(当A>1时)或缩短(当0< A<1时)到原来的A倍(横坐标不变)而得到的.
A的大小决定这个函数的最大(小)值
y=Asinx,x?R的值域是[-A, A],
最大值是A,最小值是-A.
总结
方法1:
方法1:(按 先平移后变周期的顺序变换)
y=sinx
y=sin(x+?)
横坐标缩短?>1 (伸长0y=sin(?x+?)
纵坐标伸长A>1 (缩短0
y=sinx
y=Asin(?x+?)
总结:
向左?>0 (向右?<0)
方法1:按先平移后变周期的顺序变换
平移|?|个单位
纵坐标不变
横坐标不变
步骤1
步骤2
步骤3
步骤4
步骤5
沿x轴 平行移动
横坐标 伸长或缩短
纵坐标 伸长或缩短
沿x轴 扩展
2?
?
方法2:
方法2:(按先变周期后平移顺序变换)
y=sinx
横坐标缩短?>1 (伸长0y=sin?x
纵坐标伸长A>1 (缩短0
y=sinx
y=Asin(?x+?)
总结:
纵坐标不变
横坐标不变
方法2:按先变周期后平移顺序变换
向左?>0 (向右?<0)
平移|?|/?个单位
物理中
例2:右图是某简谐运动的图象。
(1)这个简谐运动
的振幅、周期与
频率各是多少?
(2)从O点算起,到曲线上的哪一点,表示完成了一次往复运动?如从A点算起呢?
(3)求这个简谐运动的函数表达式.
例3:已知函数y=Asin(?x+?)(?>0, A>0)
的图像如下:
求解析式?
练习:如图,某地一天从6~14时的温度变化曲线近似满足函数:
这段曲线对应的函数是什么?
总结:求函数 的方法。
“第一点”为:
“第二点”为:
“第三点”为:
“第四点”为:
“第五点”为:
1. 要得到函数 y= 2 sin x 的图象,只需将 y= sinx 图象( )
A.横坐标扩大原来的两倍 B. 纵坐标扩大原来的两倍
C.横坐标扩大到原来的两倍 D. 纵坐标扩大到原来的两倍
2. 要得到函数 y=sin3x 的图象,只需将 y=sinx 图象( )
A. 横坐标扩大原来的3倍 B.横坐标扩大到原来的3倍
C. 横坐标缩小原来的1/3倍 D.横坐标缩小到原来的1/3倍
3. 要得到函数 y=sin(x + π/3)的图象,只需将 y=sinx 图象( )
A. 向左平移π/6个单位 B. 向右平移π/6个单位
C. 向左平移π/3个单位 D. 向右平移π/3个单位
4. 要得到函数 y=sin(2x-π/3)的图象,只需将y=sin2x图象( )
A. 向左平移π/3 个单位 B. 向右平移π/3个单位
C. 向左平移π/ 6个单位 D. 向右平移π/6 个单位
D
D
C
D
练习
C
B
C
D
C
A
关键:
小结
所有的点向左(? >0)
或向右(? <0)平行移动
| ? | 个单位长度
y=sinx
y=sin(x+?)
y=sinx
y=sin?x
横坐标缩短(?>1)或
伸长(0< ?<1) 1/?倍
纵坐标不变
y=sinx
y=Asinx
纵坐标伸长(A>1)或
缩短(0< A<1) A倍
横坐标不变
y=Asin(?x+ ?)
y=sinx
