人教A版高中数学必修4课件:1.3三角函数的诱导公式(共23张PPT)
文档属性
| 名称 | 人教A版高中数学必修4课件:1.3三角函数的诱导公式(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-12 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
情境问题
1 .三角函数的定义
2.终边相同的角的三角函数值有什么关系?
sin(α+2kπ) = sinα (k∈Z)
cos(α+2kπ) = cosα(k∈Z)
tan(α+2kπ) = tanα(k∈Z)
公式一
给定一个角α
(1)终边与角α的终边关于原点对称的角与α有什么关系?
它们的三角函数之间有什么关系?
P(-x, - y)
公式二
sin(π+α) =-sinα
cos(π+α) =-cosα
tan(π+α) = tanα
数学探究
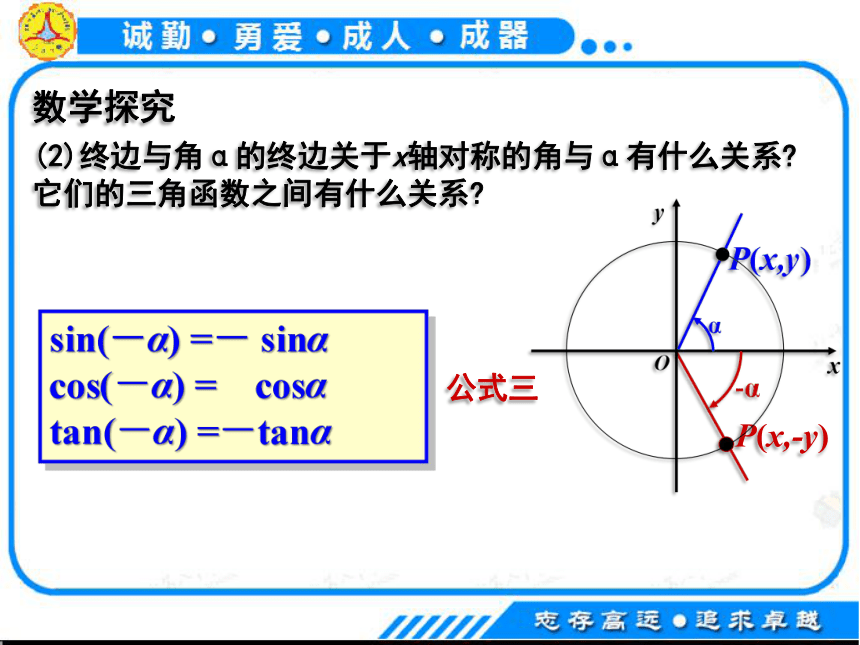
(2)终边与角α的终边关于x轴对称的角与α有什么关系?它们的三角函数之间有什么关系?
sin(-α) =- sinα
cos(-α) = cosα
tan(-α) =-tanα
公式三
P(x,-y)
数学探究
练习
将下列三角函数转化为锐角三角函数,并填在题中横线上
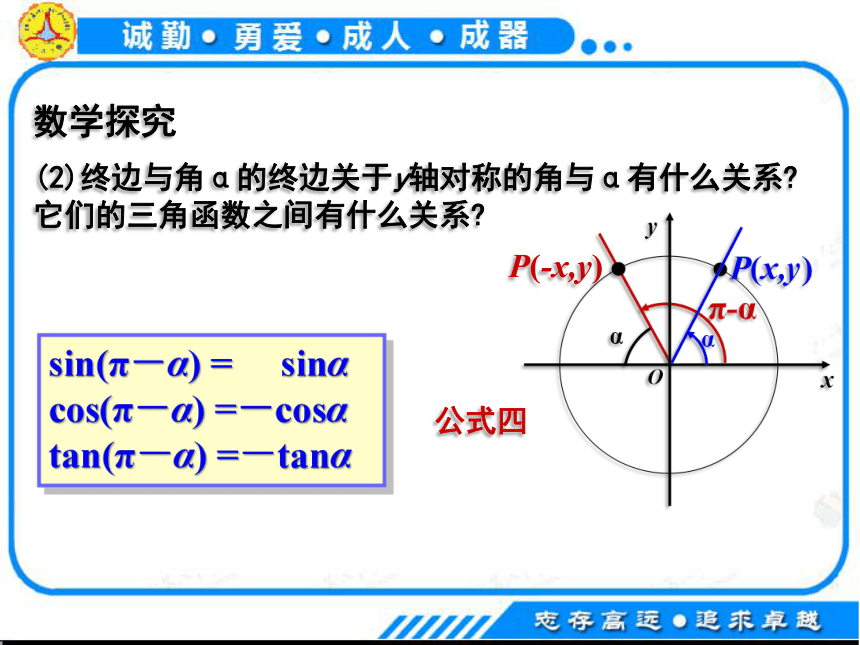
(2)终边与角α的终边关于y轴对称的角与α有什么关系?它们的三角函数之间有什么关系?
P(-x,y)
数学探究
α+k·2π(k∈Z),
-α,π±α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.
数学建构
函数名不变
符号看象限
例1.利用公式求下列三角函数值:
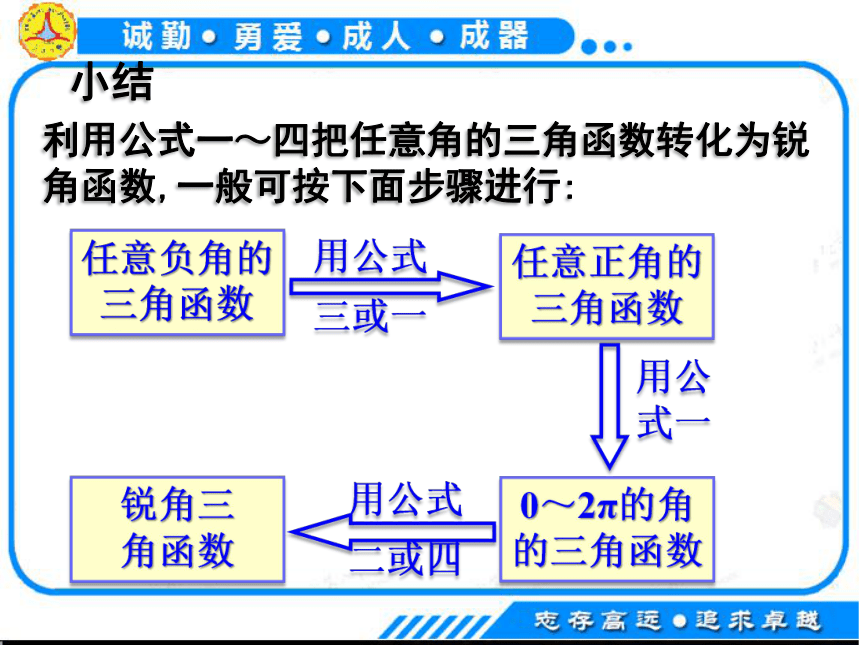
利用公式一~四把任意角的三角函数转化为锐角函数,一般可按下面步骤进行:
任意负角的
三角函数
小结
练习
利用公式求下列三角函数值:
例2 化简
练习
化简
(3)终边与角α的终边关于直线y=x对称的角与α有什么关系?它们的三角函数之间有什么关系?
P(y,x)
由公式四和公式五得
公式一~公式六叫到诱导公式
例3 证明 :
例3 证明 :
例4 化简
填表:
α
sinα
cosα
tanα
将下列三角函数转化为锐角三角函数,并填在题中横线上:
化简
化简
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
小结
三角函数的诱导公式
情境问题
1 .三角函数的定义
2.终边相同的角的三角函数值有什么关系?
sin(α+2kπ) = sinα (k∈Z)
cos(α+2kπ) = cosα(k∈Z)
tan(α+2kπ) = tanα(k∈Z)
公式一
给定一个角α
(1)终边与角α的终边关于原点对称的角与α有什么关系?
它们的三角函数之间有什么关系?
P(-x, - y)
公式二
sin(π+α) =-sinα
cos(π+α) =-cosα
tan(π+α) = tanα
数学探究
(2)终边与角α的终边关于x轴对称的角与α有什么关系?它们的三角函数之间有什么关系?
sin(-α) =- sinα
cos(-α) = cosα
tan(-α) =-tanα
公式三
P(x,-y)
数学探究
练习
将下列三角函数转化为锐角三角函数,并填在题中横线上
(2)终边与角α的终边关于y轴对称的角与α有什么关系?它们的三角函数之间有什么关系?
P(-x,y)
数学探究
α+k·2π(k∈Z),
-α,π±α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.
数学建构
函数名不变
符号看象限
例1.利用公式求下列三角函数值:
利用公式一~四把任意角的三角函数转化为锐角函数,一般可按下面步骤进行:
任意负角的
三角函数
小结
练习
利用公式求下列三角函数值:
例2 化简
练习
化简
(3)终边与角α的终边关于直线y=x对称的角与α有什么关系?它们的三角函数之间有什么关系?
P(y,x)
由公式四和公式五得
公式一~公式六叫到诱导公式
例3 证明 :
例3 证明 :
例4 化简
填表:
α
sinα
cosα
tanα
将下列三角函数转化为锐角三角函数,并填在题中横线上:
化简
化简
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
小结
三角函数的诱导公式
