2.4 理想气体状态方程:40张PPT
文档属性
| 名称 | 2.4 理想气体状态方程:40张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 717.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-12-10 15:45:20 | ||
图片预览








文档简介
课件40张PPT。2.4 理想气体状态方程历史回顾【问题1】三大气体实验定律内容是什么?公式: pV =C12、査理定律:1、玻意耳定律:3、盖-吕萨克定律:【问题2】这些定律的适用范围是什么?温度不太低,压强不太大.【问题3】如果某种气体的三个状态参量(p、V、T)都发生了变化,它们之间又遵从什么规律呢?一.理想气体理想气体具有那些特点呢?1、理想气体是不存在的,是一种理想模型。2、在温度不太低,压强不太大时实际气体都可看成是理想气体。1、理想气体:
理想气体是实际气体的一种理想模型.微观上就是不考虑分子本身的体积和分子间相互作用力的气体。宏观上就是始终能遵守
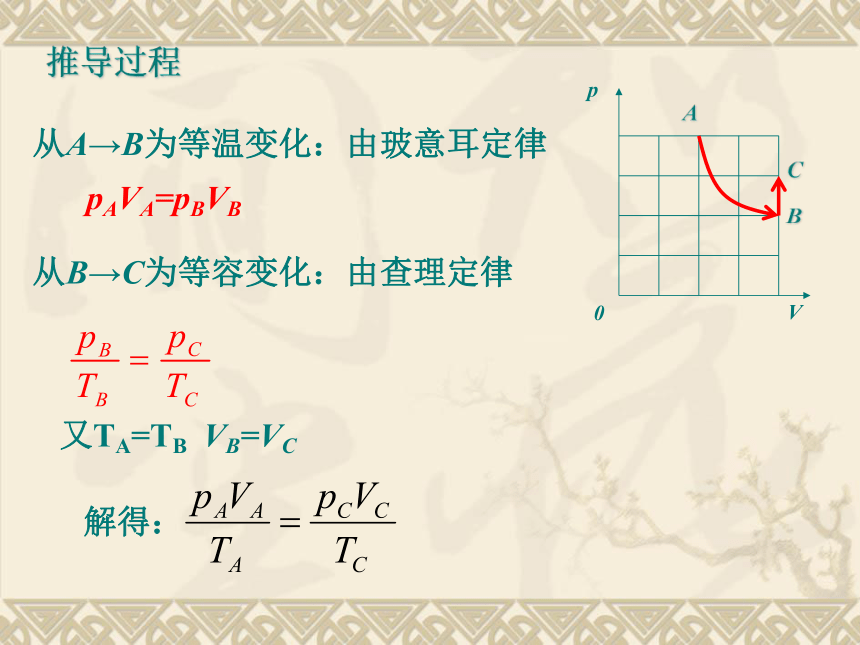
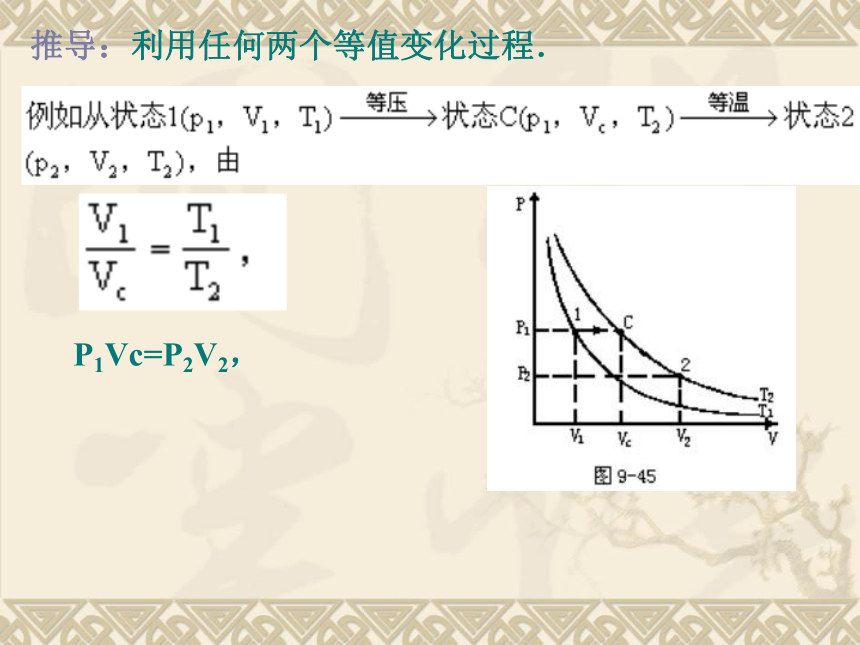
的气体.许多实际气体,在通常的温度和压强下,它们的性质都近似于理想气体 一定质量的理想气体的内能仅由温度决定 ,与气体的体积无关.4、从能量上说:理想气体的微观本质是忽略了分子力,没有分子势能,理想气体的内能只有分子动能。3、从微观上说:分子间以及分子和器壁间,除碰撞外无其他作用力,分子本身没有体积,即它所占据的空间认为都是可以被压缩的空间。思考与讨论如图所示,一定质量的某种理想气体从A到B经历了一个等温过程,从B到C经历了一个等容过程。分别用pA、VA、TA和pB、VB、TB以及pC、VC、TC表示气体在A、B、C三个状态的状态参量,那么A、C状态的状态参量间有何关系呢?推导过程从A→B为等温变化:由玻意耳定律pAVA=pBVB从B→C为等容变化:由查理定律又TA=TB VB=VC解得:推导:利用任何两个等值变化过程. P1Vc=P2V2, 推论:
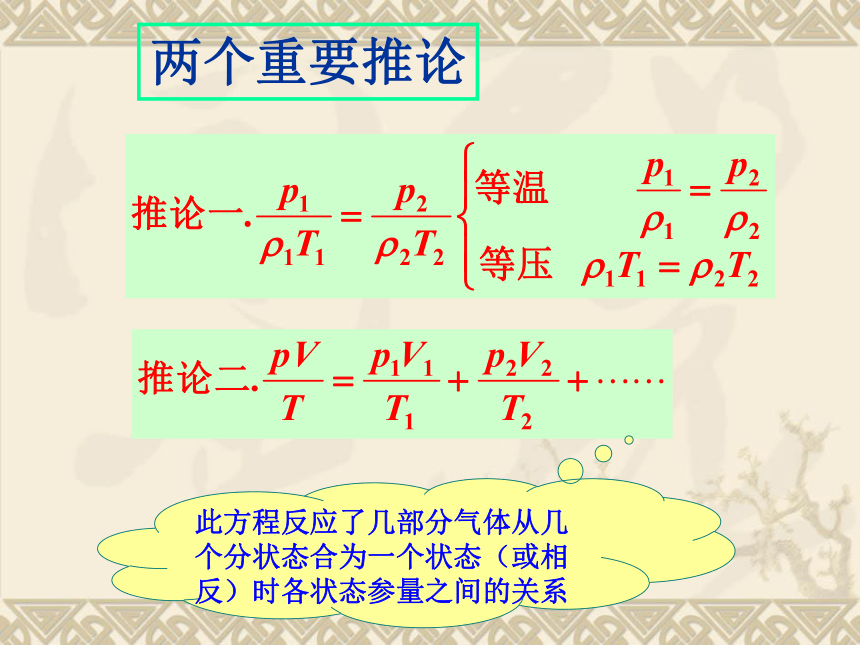
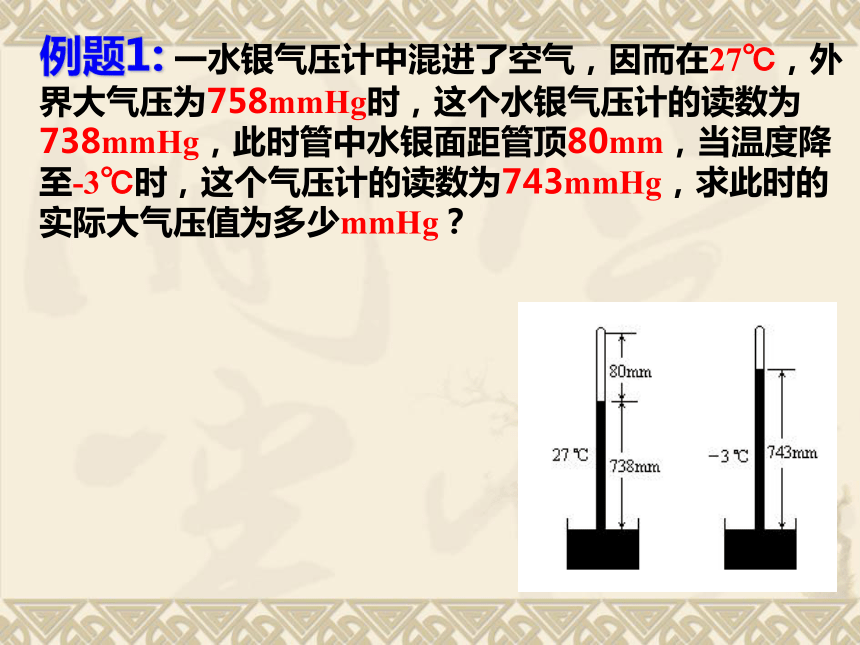
1.当状态变化过程中保持:某一个参量不变时,就可从气态方程分别得到玻意耳定律、查理定律、盖·吕萨克定律. 两个重要推论此方程反应了几部分气体从几个分状态合为一个状态(或相反)时各状态参量之间的关系二、理想气体的状态方程1、内容:一定质量的某种理想气体在从一个状态变化到另一个状态时,尽管p、V、T都可能改变,但是压强跟体积的乘积与热力学温度的比值保持不变。2、公式:3、使用条件:一定质量的某种理想气体.注:恒量C由理想气体的质量和种类决定,即由理想气体的物质的量决定例题1:?一水银气压计中混进了空气,因而在27℃,外界大气压为758mmHg时,这个水银气压计的读数为738mmHg,此时管中水银面距管顶80mm,当温度降至-3℃时,这个气压计的读数为743mmHg,求此时的实际大气压值为多少mmHg?p1=758-738=20mmHg? V1=80Smm3 T1=273+27=300 KT2=273+(-3)=270K解得:? p=762.2 mmHgp2=p-743mmHg V2=(738+80)S-743S=75Smm3解:以混进水银气压计的空气为研究对象初状态:末状态:由理想气体状态方程得:4、气体密度式:以1mol的某种理想气体为研究对象,它在标准状态 设 为1mol理想气体在标准状态下的
常量,叫做摩尔气体常量. 注意:R的数值与单位的对应P(atm),V (L): R=0.082 atm·L/mol·KP(Pa),V (m3): R=8.31 J/mol·K一摩尔理想气体的状态方程 :5、摩尔气体常量:例:教室的容积是100m3,在温度是7℃,大气压强为1.0×105Pa时,室内空气的质量是130kg,当温度升高到27℃时大气压强为1.2×105Pa时,教室内空气质量是多少?理想气体的状态方程的应用解:初态:P1=1.0×105pa,V1=100m3,T1=273+7=280K
末态:P2=1.2×105Pa,V2=?,T2=300K
根据理想气体状态方程:说明有气体流入房间例:一定质量的理想气体处于某一初始状态,现要使它的温度经过状态变化后,回到初始状态的温度,下列过程可以实现的是[ ]
A.先保持压强不变而使体积膨胀,接着保持体积不变而减小压强
B.先保持压强不变而使体积减小,接着保持体积不变而减小压强
C.先保持体积不变而增大压强,接着保持压强不变而使体积膨胀
D.先保持体积不变而减小压强,接着保持压强不变而使体积减小
A三、克拉珀龙方程克拉珀龙方程是任意质量的理想气体的状态方程,它联系着某一确定状态下,各物理量的关系。对实际气体只要温度不太低,压强不太大就可应用克拉珀龙方程解题.任意质量的理想气体状态方程:PV=nRT
(1)n为物质的量,R=8.31J/mol.k——摩尔气体恒量
(2)该式是任意质量的理想气体状态方程,又叫克拉帕龙方程如图所示,一定质量的理想气体,由状态A沿直线AB变化到B,在此过程中,气体分子的平均速率的变化情况是( )练习:A、不断增大B、不断减小C、先减小后增大D、先增大后减小D理想气体状态方程的应用要点
1)选对象——根据题意,选出所研究的某一部分气体.这部分气体在状态变化过程中,其质量必须保持一定.
2)找参量——找出作为研究对象的这部分气体发生状态变化前后的一组T、p、V数值或表达式.其中压强的确定往往是个关键,需注意它的一些常见情况(参见第一节),并结合力学知识(如力平衡条件或牛顿运动定律)才能写出表达式.
3)认过程——过程表示两个状态之间的一种变化方式,除题中条件已直接指明外,在许多情况下,往往需要通过对研究对象跟周围环境的相互关系的分析中才能确定.认清变化过程这是正确选用物理规律的前提.
4)列方程——根据研究对象状态变化的具体方式,选用气态方程或某一实验定律.代入具体数值时,T必须用热力学温度,p、V两个量只需方程两边对应一致.
练习:粗细均匀的,一端开口、一端封闭的细玻璃管中,有质量为10mg的某种理想气体,被长为h=16cm的水银柱封闭在管中,当玻璃管开口向上,竖直插在冰水中时,管内气柱的长度L=30cm.如图所示.若将玻璃管从冰水中取出后,颠倒使其竖直开口向下,温度升高到27℃(已知大气压强为75cmHg).试求:(1)若玻璃管太短,颠倒时溢出一些水银,水银与管口齐平,但气体没有泄漏,气柱长度变为50cm,则管长为多少?(2)若玻璃管足够长,水银未溢出,但溢出一些气体,气柱长变为30cm,则逸出气体的质量是多少?(1)玻璃管长度l=50+15=65cm
(2)逸出的气体的质量△m=m1-m2=4.1mg例:一圆柱形气缸直立在地面上,内有一个有质量、无摩擦的绝热活塞,把气缸分成容积相同的A、B两部分,如图两部分气体的温度相同,均为T0=27℃,A部分气体的压强PA0=1.0×105Pa,B部分气体的压强PB0=2.0×105pa.现对B部分气体加热,使活塞上升,保持A部分气体的温度不变,使A部分气体的体积减小为原来的2/3.求此时:
(1)A部分气体的压强PA.
(2)B部分气体的温度TB.PA=1.5×105Pa TB=500K分析:A气体做等温变化,
B气体三个参量均发生变化
A、B之间的联系:
1、体积之和不变
2、压强差不变练习:护士为病人输液时,必须排尽输液管中的空气,否则空气泡进入血管后会随着血液向前流动, 而当流到口径较细的血管时,会出现“栓塞”阻碍血液的流动,造成严重的医疗事故。某病人的体温为37℃,舒张压为80mmHg,收缩压为120mmHg,假设一护士在为病人输液时,一时疏忽将一个大气压,体积为0.01cm3,温度为27℃的空气泡打入静脉血管,当空气泡随血液流到横截面积为1mm2的血管时,产生“栓塞”的最小长度为多少?6.54cm巩固练习:
1、在截面积S=1cm2,两端封闭粗细均匀的玻璃管中央,有一段水银柱,A、B两部分空气柱长l1=l′1=40cm.左端为7℃,右端为17℃时,求:
(1)左边也上升到17℃时,水银柱会向何处移动?移动多少?水银柱会向右移 (2)左、右两边都升高10℃时,水银柱是否移动?为什么? 若l1≠l2呢?
若是同时降温呢?
若玻璃管处于竖直放置情况呢?A2、如图8-9所示,透热汽缸A被活塞封闭一定质量气体,其体积VA=4.8L,活塞另一边与大气相通.汽缸与透热容器B相连,体积VB=2.4L,置于恒温箱中,汽缸A与容器B相连的细管(体积不计且绝热)中间有阀门K将两部分分开.已知,环境温度为27℃,恒温箱的温度为127℃.今将阀门K打开,汽缸中最后气体的体积多大?
3、如图8-10所示,一端开口的均匀玻璃管内,一段水银柱封闭着一段空气柱.当温度为27℃时,气柱长10cm,右侧水银柱比左侧水银柱高2cm,比玻璃管开口位置高1cm.当温度升高到100℃时,封闭的气柱有多长?(大气压相当76cm水银柱产生的压强.)
由题意可知,变化后温度为100℃大于66℃,所以变化后右侧水银面低于左侧水银面,设低x厘米.则变化后气柱状态为
例:如图所示,开口向上的玻璃管长L=100cm,内有一段水银柱高h=20cm,封闭着长a=50cm、温度为27 ℃的空气柱。已知大气压强为p0=76cmHg,则气柱温度至少应达到多少才可使水银全部溢出? 提示:开始水银作等压膨胀,以后P,V,T三者发生变化,对应的PV乘积最大处温度最高,这就是水银要全部溢出对应的最低温度例:实验室内备有米尺、天平、量筒、温度计、气压计等器材,需选取哪几件最必备的器材,测量哪几个数据,即可根据物理常数表和气体定律估算出教室内现有的空气分子数?写出表达式.
需选取米尺、温度计、气压计三件器材.
用米尺测出教室的长、宽、高,算出体积V;用温度计测出室温,设为T;用气压计读出大气压,设为p. 理想气体状态方程的综合应用 气体问题中,结合力学知识有两类典型的综合题,一是力平衡,二是加速运动.研究时,常需分别选取研究对象,沿着不同的线索考虑.对力学对象(如气缸、活塞、容器、水银滴等)需通过受力分析,列出平衡方程或牛顿运动方程;对气体对象,根据状态参量,列出气态方程(或用气体实验定律).
例:如图,两个内径不同的圆筒组成一个气缸,里面各有一个活塞A、B.其横截面积分别为SA=10cm2和SB=4cm2.质量分别为mA=6kg,mB=4kg,它们之间用一质量不计的细杆相连.两活塞均可在气缸内无摩擦滑动,但不漏气.在气温是-23℃时,用销子P把活塞B锁住.此时缸内气体体积为300cm3,气压为105Pa.由于圆筒传热性好,经过一段时间,气体温度升至室温27℃,并保持不变,外界大气压P0=105Pa,此后将销子P拔去.求:(1)将销子P拔去时两活塞(含杆)的加速度;(2)活塞在各自圆筒范围内运动多大一段距离后,它们的速度可达最大值(设气体温度保持不变)? a=1.2m/s2,方向水平向左
X=10cm 巩固练习:1、 由两个传热性能很好的直径不同的圆筒组成的装置如图9-64所示.在两个圆筒内各有一个活塞,其截面积分别为SA=200cm2,SB=40cm2.两活塞可以分别在两圆筒内无磨擦地运动且不漏气,其间用长l=99.9cm的硬质轻杆相连,两活塞外侧与大气相通,大气压强P0=105Pa.将两个圆筒水平固定后用水平力F=5000N向右作用在活塞A上,活塞B上不加外力,恰能使两活塞间气体都移到小圆筒中;若撤去活塞A上外力,在活塞B上加一水平向左外力F′,恰能将两活塞间气体都移到大圆筒中,求F′. 2、如图8-21所示,由两个共轴的半径不同的圆筒联接成的汽缸竖直放置,活塞A、B的截面积SA、SB分别为20cm2、10cm2.在A、B之间封闭着一定质量的理想气体.今用长为2L的细线将A和B相连,它们可以在缸内无摩擦地上下活动.A的上方与B的下方与大气相通,大气压强为105Pa.(1)在图中所示位置,A、B处于平衡,已知这时缸内气体的温度是600K,气体压强1.2×105Pa,活塞B的质量mB=1kg,g=10m/s2.求活塞A的质量mA.1kg ②汽缸内气体的温度由600K缓慢地下降,活塞A、B将一起缓慢地下移.当A无法下移后,气温仍继续下降,直到A、B间的距离开始缩小为止.请分析在这过程中气体所经历的状态变化的情况,并求缸内气体的最低温度Tmin.
300K 3.如图17-25所示,汽缸竖直放置、汽缸内的活塞面积S=1cm2,质量m=200g.开始时,汽缸内被封闭气体的压强P1=2×105Pa,温度T1=480,活塞到汽缸底部的距离H1=12cm.拔出止动销钉(汽缸不漏气),活塞向上无摩擦滑动.当它达到最大速度时,缸内气体的温度T2=300K.此时活塞距汽缸底部的距离H2有多大?已知大气压强P0=1.0×105Pa. H2=12.5cm. 4、如图8-37所示,底面积为S=100cm2,深为h=8cm的圆筒容器A,用一细管与容器B连接,K为开关,开始时,B为真空,A敞开,K关闭,一个重为600N的活塞,恰能封住容器A,并能在容器内无摩擦地滑动.设大气压强为1×105Pa,活塞厚度不计.
(1)将活塞放在A的开口端后放手,活塞下降后又平衡,求下降深度.
(2)打开K,将A、B倒置,使A开口向下,B的容积至少多大活塞才不掉下来?
(1)H=5cm
(2) hB=12cm 如图所示,在竖直加速上升的密闭人造卫星内有一水银气压计,卫星开始上升前,卫星内气温为0℃,气压计水银柱高76 cm;在上升至离地面不太高的高度时,卫星内气温为27.3℃,此时水银气压计水银柱高41.8cm,试问,这时卫星的加速度为多少?充满氢气的橡皮球,球壳的质量是球内所充氢气质量的3倍,在标准状态下空气密度与氢气密度之比是29∶2。现在球内氢气的压强是球外空气压强的1.5倍,球内外温度都是0℃。问氢气开始上升时的加速度是多少? 定性判断容器内液柱移动方向问题如图所示,两端封闭粗细均匀、竖直放置的玻璃管内有一长为h的水银柱,将管内气体分为两部分。已知l2=2l1,若将两部分气体升高相同的温度,管内水银柱将如何将移动?(设原来温度相同)定性判断容器内液柱移动方向常用方法:假设法极限法公式法图像法小结:一、理想气体:在任何温度和任何压强下都能严格地遵从气体实验定律的气体二、理想气体的状态方程注:恒量C由理想气体的质量和种类决定,即由气体的物质的量决定气体密度式:三、克拉珀龙方程摩尔气体常量:P(atm),V (L): R=0.082 atm·L/mol·KP(Pa),V (m3): R=8.31 J/mol·K
理想气体是实际气体的一种理想模型.微观上就是不考虑分子本身的体积和分子间相互作用力的气体。宏观上就是始终能遵守
的气体.许多实际气体,在通常的温度和压强下,它们的性质都近似于理想气体 一定质量的理想气体的内能仅由温度决定 ,与气体的体积无关.4、从能量上说:理想气体的微观本质是忽略了分子力,没有分子势能,理想气体的内能只有分子动能。3、从微观上说:分子间以及分子和器壁间,除碰撞外无其他作用力,分子本身没有体积,即它所占据的空间认为都是可以被压缩的空间。思考与讨论如图所示,一定质量的某种理想气体从A到B经历了一个等温过程,从B到C经历了一个等容过程。分别用pA、VA、TA和pB、VB、TB以及pC、VC、TC表示气体在A、B、C三个状态的状态参量,那么A、C状态的状态参量间有何关系呢?推导过程从A→B为等温变化:由玻意耳定律pAVA=pBVB从B→C为等容变化:由查理定律又TA=TB VB=VC解得:推导:利用任何两个等值变化过程. P1Vc=P2V2, 推论:
1.当状态变化过程中保持:某一个参量不变时,就可从气态方程分别得到玻意耳定律、查理定律、盖·吕萨克定律. 两个重要推论此方程反应了几部分气体从几个分状态合为一个状态(或相反)时各状态参量之间的关系二、理想气体的状态方程1、内容:一定质量的某种理想气体在从一个状态变化到另一个状态时,尽管p、V、T都可能改变,但是压强跟体积的乘积与热力学温度的比值保持不变。2、公式:3、使用条件:一定质量的某种理想气体.注:恒量C由理想气体的质量和种类决定,即由理想气体的物质的量决定例题1:?一水银气压计中混进了空气,因而在27℃,外界大气压为758mmHg时,这个水银气压计的读数为738mmHg,此时管中水银面距管顶80mm,当温度降至-3℃时,这个气压计的读数为743mmHg,求此时的实际大气压值为多少mmHg?p1=758-738=20mmHg? V1=80Smm3 T1=273+27=300 KT2=273+(-3)=270K解得:? p=762.2 mmHgp2=p-743mmHg V2=(738+80)S-743S=75Smm3解:以混进水银气压计的空气为研究对象初状态:末状态:由理想气体状态方程得:4、气体密度式:以1mol的某种理想气体为研究对象,它在标准状态 设 为1mol理想气体在标准状态下的
常量,叫做摩尔气体常量. 注意:R的数值与单位的对应P(atm),V (L): R=0.082 atm·L/mol·KP(Pa),V (m3): R=8.31 J/mol·K一摩尔理想气体的状态方程 :5、摩尔气体常量:例:教室的容积是100m3,在温度是7℃,大气压强为1.0×105Pa时,室内空气的质量是130kg,当温度升高到27℃时大气压强为1.2×105Pa时,教室内空气质量是多少?理想气体的状态方程的应用解:初态:P1=1.0×105pa,V1=100m3,T1=273+7=280K
末态:P2=1.2×105Pa,V2=?,T2=300K
根据理想气体状态方程:说明有气体流入房间例:一定质量的理想气体处于某一初始状态,现要使它的温度经过状态变化后,回到初始状态的温度,下列过程可以实现的是[ ]
A.先保持压强不变而使体积膨胀,接着保持体积不变而减小压强
B.先保持压强不变而使体积减小,接着保持体积不变而减小压强
C.先保持体积不变而增大压强,接着保持压强不变而使体积膨胀
D.先保持体积不变而减小压强,接着保持压强不变而使体积减小
A三、克拉珀龙方程克拉珀龙方程是任意质量的理想气体的状态方程,它联系着某一确定状态下,各物理量的关系。对实际气体只要温度不太低,压强不太大就可应用克拉珀龙方程解题.任意质量的理想气体状态方程:PV=nRT
(1)n为物质的量,R=8.31J/mol.k——摩尔气体恒量
(2)该式是任意质量的理想气体状态方程,又叫克拉帕龙方程如图所示,一定质量的理想气体,由状态A沿直线AB变化到B,在此过程中,气体分子的平均速率的变化情况是( )练习:A、不断增大B、不断减小C、先减小后增大D、先增大后减小D理想气体状态方程的应用要点
1)选对象——根据题意,选出所研究的某一部分气体.这部分气体在状态变化过程中,其质量必须保持一定.
2)找参量——找出作为研究对象的这部分气体发生状态变化前后的一组T、p、V数值或表达式.其中压强的确定往往是个关键,需注意它的一些常见情况(参见第一节),并结合力学知识(如力平衡条件或牛顿运动定律)才能写出表达式.
3)认过程——过程表示两个状态之间的一种变化方式,除题中条件已直接指明外,在许多情况下,往往需要通过对研究对象跟周围环境的相互关系的分析中才能确定.认清变化过程这是正确选用物理规律的前提.
4)列方程——根据研究对象状态变化的具体方式,选用气态方程或某一实验定律.代入具体数值时,T必须用热力学温度,p、V两个量只需方程两边对应一致.
练习:粗细均匀的,一端开口、一端封闭的细玻璃管中,有质量为10mg的某种理想气体,被长为h=16cm的水银柱封闭在管中,当玻璃管开口向上,竖直插在冰水中时,管内气柱的长度L=30cm.如图所示.若将玻璃管从冰水中取出后,颠倒使其竖直开口向下,温度升高到27℃(已知大气压强为75cmHg).试求:(1)若玻璃管太短,颠倒时溢出一些水银,水银与管口齐平,但气体没有泄漏,气柱长度变为50cm,则管长为多少?(2)若玻璃管足够长,水银未溢出,但溢出一些气体,气柱长变为30cm,则逸出气体的质量是多少?(1)玻璃管长度l=50+15=65cm
(2)逸出的气体的质量△m=m1-m2=4.1mg例:一圆柱形气缸直立在地面上,内有一个有质量、无摩擦的绝热活塞,把气缸分成容积相同的A、B两部分,如图两部分气体的温度相同,均为T0=27℃,A部分气体的压强PA0=1.0×105Pa,B部分气体的压强PB0=2.0×105pa.现对B部分气体加热,使活塞上升,保持A部分气体的温度不变,使A部分气体的体积减小为原来的2/3.求此时:
(1)A部分气体的压强PA.
(2)B部分气体的温度TB.PA=1.5×105Pa TB=500K分析:A气体做等温变化,
B气体三个参量均发生变化
A、B之间的联系:
1、体积之和不变
2、压强差不变练习:护士为病人输液时,必须排尽输液管中的空气,否则空气泡进入血管后会随着血液向前流动, 而当流到口径较细的血管时,会出现“栓塞”阻碍血液的流动,造成严重的医疗事故。某病人的体温为37℃,舒张压为80mmHg,收缩压为120mmHg,假设一护士在为病人输液时,一时疏忽将一个大气压,体积为0.01cm3,温度为27℃的空气泡打入静脉血管,当空气泡随血液流到横截面积为1mm2的血管时,产生“栓塞”的最小长度为多少?6.54cm巩固练习:
1、在截面积S=1cm2,两端封闭粗细均匀的玻璃管中央,有一段水银柱,A、B两部分空气柱长l1=l′1=40cm.左端为7℃,右端为17℃时,求:
(1)左边也上升到17℃时,水银柱会向何处移动?移动多少?水银柱会向右移 (2)左、右两边都升高10℃时,水银柱是否移动?为什么? 若l1≠l2呢?
若是同时降温呢?
若玻璃管处于竖直放置情况呢?A2、如图8-9所示,透热汽缸A被活塞封闭一定质量气体,其体积VA=4.8L,活塞另一边与大气相通.汽缸与透热容器B相连,体积VB=2.4L,置于恒温箱中,汽缸A与容器B相连的细管(体积不计且绝热)中间有阀门K将两部分分开.已知,环境温度为27℃,恒温箱的温度为127℃.今将阀门K打开,汽缸中最后气体的体积多大?
3、如图8-10所示,一端开口的均匀玻璃管内,一段水银柱封闭着一段空气柱.当温度为27℃时,气柱长10cm,右侧水银柱比左侧水银柱高2cm,比玻璃管开口位置高1cm.当温度升高到100℃时,封闭的气柱有多长?(大气压相当76cm水银柱产生的压强.)
由题意可知,变化后温度为100℃大于66℃,所以变化后右侧水银面低于左侧水银面,设低x厘米.则变化后气柱状态为
例:如图所示,开口向上的玻璃管长L=100cm,内有一段水银柱高h=20cm,封闭着长a=50cm、温度为27 ℃的空气柱。已知大气压强为p0=76cmHg,则气柱温度至少应达到多少才可使水银全部溢出? 提示:开始水银作等压膨胀,以后P,V,T三者发生变化,对应的PV乘积最大处温度最高,这就是水银要全部溢出对应的最低温度例:实验室内备有米尺、天平、量筒、温度计、气压计等器材,需选取哪几件最必备的器材,测量哪几个数据,即可根据物理常数表和气体定律估算出教室内现有的空气分子数?写出表达式.
需选取米尺、温度计、气压计三件器材.
用米尺测出教室的长、宽、高,算出体积V;用温度计测出室温,设为T;用气压计读出大气压,设为p. 理想气体状态方程的综合应用 气体问题中,结合力学知识有两类典型的综合题,一是力平衡,二是加速运动.研究时,常需分别选取研究对象,沿着不同的线索考虑.对力学对象(如气缸、活塞、容器、水银滴等)需通过受力分析,列出平衡方程或牛顿运动方程;对气体对象,根据状态参量,列出气态方程(或用气体实验定律).
例:如图,两个内径不同的圆筒组成一个气缸,里面各有一个活塞A、B.其横截面积分别为SA=10cm2和SB=4cm2.质量分别为mA=6kg,mB=4kg,它们之间用一质量不计的细杆相连.两活塞均可在气缸内无摩擦滑动,但不漏气.在气温是-23℃时,用销子P把活塞B锁住.此时缸内气体体积为300cm3,气压为105Pa.由于圆筒传热性好,经过一段时间,气体温度升至室温27℃,并保持不变,外界大气压P0=105Pa,此后将销子P拔去.求:(1)将销子P拔去时两活塞(含杆)的加速度;(2)活塞在各自圆筒范围内运动多大一段距离后,它们的速度可达最大值(设气体温度保持不变)? a=1.2m/s2,方向水平向左
X=10cm 巩固练习:1、 由两个传热性能很好的直径不同的圆筒组成的装置如图9-64所示.在两个圆筒内各有一个活塞,其截面积分别为SA=200cm2,SB=40cm2.两活塞可以分别在两圆筒内无磨擦地运动且不漏气,其间用长l=99.9cm的硬质轻杆相连,两活塞外侧与大气相通,大气压强P0=105Pa.将两个圆筒水平固定后用水平力F=5000N向右作用在活塞A上,活塞B上不加外力,恰能使两活塞间气体都移到小圆筒中;若撤去活塞A上外力,在活塞B上加一水平向左外力F′,恰能将两活塞间气体都移到大圆筒中,求F′. 2、如图8-21所示,由两个共轴的半径不同的圆筒联接成的汽缸竖直放置,活塞A、B的截面积SA、SB分别为20cm2、10cm2.在A、B之间封闭着一定质量的理想气体.今用长为2L的细线将A和B相连,它们可以在缸内无摩擦地上下活动.A的上方与B的下方与大气相通,大气压强为105Pa.(1)在图中所示位置,A、B处于平衡,已知这时缸内气体的温度是600K,气体压强1.2×105Pa,活塞B的质量mB=1kg,g=10m/s2.求活塞A的质量mA.1kg ②汽缸内气体的温度由600K缓慢地下降,活塞A、B将一起缓慢地下移.当A无法下移后,气温仍继续下降,直到A、B间的距离开始缩小为止.请分析在这过程中气体所经历的状态变化的情况,并求缸内气体的最低温度Tmin.
300K 3.如图17-25所示,汽缸竖直放置、汽缸内的活塞面积S=1cm2,质量m=200g.开始时,汽缸内被封闭气体的压强P1=2×105Pa,温度T1=480,活塞到汽缸底部的距离H1=12cm.拔出止动销钉(汽缸不漏气),活塞向上无摩擦滑动.当它达到最大速度时,缸内气体的温度T2=300K.此时活塞距汽缸底部的距离H2有多大?已知大气压强P0=1.0×105Pa. H2=12.5cm. 4、如图8-37所示,底面积为S=100cm2,深为h=8cm的圆筒容器A,用一细管与容器B连接,K为开关,开始时,B为真空,A敞开,K关闭,一个重为600N的活塞,恰能封住容器A,并能在容器内无摩擦地滑动.设大气压强为1×105Pa,活塞厚度不计.
(1)将活塞放在A的开口端后放手,活塞下降后又平衡,求下降深度.
(2)打开K,将A、B倒置,使A开口向下,B的容积至少多大活塞才不掉下来?
(1)H=5cm
(2) hB=12cm 如图所示,在竖直加速上升的密闭人造卫星内有一水银气压计,卫星开始上升前,卫星内气温为0℃,气压计水银柱高76 cm;在上升至离地面不太高的高度时,卫星内气温为27.3℃,此时水银气压计水银柱高41.8cm,试问,这时卫星的加速度为多少?充满氢气的橡皮球,球壳的质量是球内所充氢气质量的3倍,在标准状态下空气密度与氢气密度之比是29∶2。现在球内氢气的压强是球外空气压强的1.5倍,球内外温度都是0℃。问氢气开始上升时的加速度是多少? 定性判断容器内液柱移动方向问题如图所示,两端封闭粗细均匀、竖直放置的玻璃管内有一长为h的水银柱,将管内气体分为两部分。已知l2=2l1,若将两部分气体升高相同的温度,管内水银柱将如何将移动?(设原来温度相同)定性判断容器内液柱移动方向常用方法:假设法极限法公式法图像法小结:一、理想气体:在任何温度和任何压强下都能严格地遵从气体实验定律的气体二、理想气体的状态方程注:恒量C由理想气体的质量和种类决定,即由气体的物质的量决定气体密度式:三、克拉珀龙方程摩尔气体常量:P(atm),V (L): R=0.082 atm·L/mol·KP(Pa),V (m3): R=8.31 J/mol·K
同课章节目录
- 第一章用统计思想研究分子运动
- 1.1一种新的研究方法
- 1.2走过分子世界
- 1.3 分子热运动
- 1.4无序中的有序
- 1.5用统计思想解释分子运动的宏观表现
- 1.6物体的内能
- 第二章气体定律与人类生活
- 2.1气体的状态
- 2.2玻意耳定律
- 2.3查理定律和盖·吕萨克定律
- 2.4 理想气体状态方程
- 2.5空气的湿度与人类生活
- 第三章固体、液体与新材料
- 3.1研究固体的性质
- 3.2研究液体的表面性质
- 3.3液晶与显示器
- 3.4半导体材料和纳米材料
- 第四章热力学定律与能量守恒
- 4.1热力学第一定律
- 4.2能量守恒定律的发现历程
- 4.3热力学第二定律
- 4.4描述无序程度的物理量
- 第五章能源与可持续发展
- 5.1能源利用与环境污染
- 5.2能源开发与环境保护
- 5.3节约能源、保护资源与可持续发展
