人教版九年级数学下册28.1锐角三角函数 教学设计
文档属性
| 名称 | 人教版九年级数学下册28.1锐角三角函数 教学设计 |  | |
| 格式 | zip | ||
| 文件大小 | 226.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-12 12:47:58 | ||
图片预览


文档简介
课题: 锐角三角函数(第一课时)
教材:人教版九年级下册28.1
【教学目标】
1. 经历回顾及提出问题的过程,能将实际问题转化为几何模型,感悟研究直角三角形边角关系的重要性.
2. 参与锐角三角函数定义的活动过程,会计算特殊角对应边的比值,能结合图形陈述锐角三角函数概念、表示方法、取值范围,体会概念形成过程和所蕴含的归纳、类比思想.
3. 通过求锐角三角函数值的活动,掌握特殊角的三角函数值,积累求锐角三角函数值的数学活动经验.
【教学重难点】
教学重点:通过求锐角三角函数值的活动,掌握特殊角的三角函数值,能用锐角三角函数解直角三角形.
教学难点:探索并认识锐角三角函数.
【教学方法与教学手段】
教学方法:自学.议论.引导教学法.
教学手段:利用生活中的实例引入教学,抽象出要解决的问题,师生共同探究归纳总结生成结论.
【教学过程】
1、 情境导入
活动1
问题 如图,为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使水管出水口到水平面的高度为35m,那么需准备多长的管?
导图
【设计意图】对这样实际问题,教师引导学生如何将这一实际问题转化为数学模型,让学生在相互交流中获得结论.教师重点关注学生获取结论的过程,即是否运用“ = ”这一结论.
二、师生议学
探究1
问题 如果将上述问题中出水口到水平面的高度改为50m,那么需准备多长的水管?通过对前面问题和探究的思考,你有什么发现?
【设计意图】在学生自主探究,获得结论后,让他们相互交流各自体会,为掌握本节知识积累感性认识.最后教师与学生一道进行简要总结.
【归纳结论】在一个直角三角形中,如果一个锐角为30°,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于,是一个定值.
探究2
问题 如图1,如果将上述问题中的斜坡与水平面所成角的度数改成固定角度α,那么这个角的对边和斜边的比值还是定值吗?
图1
【设计意图】由特殊到一般的推理,学生可以利用相似三角形的性质发现当Bi点在射线AB上移动时,每个直角三角形中锐角对边和斜边的比值是定值.
【归纳结论】直角三角形中,锐角的对边和斜边的比值是定值.
探究3
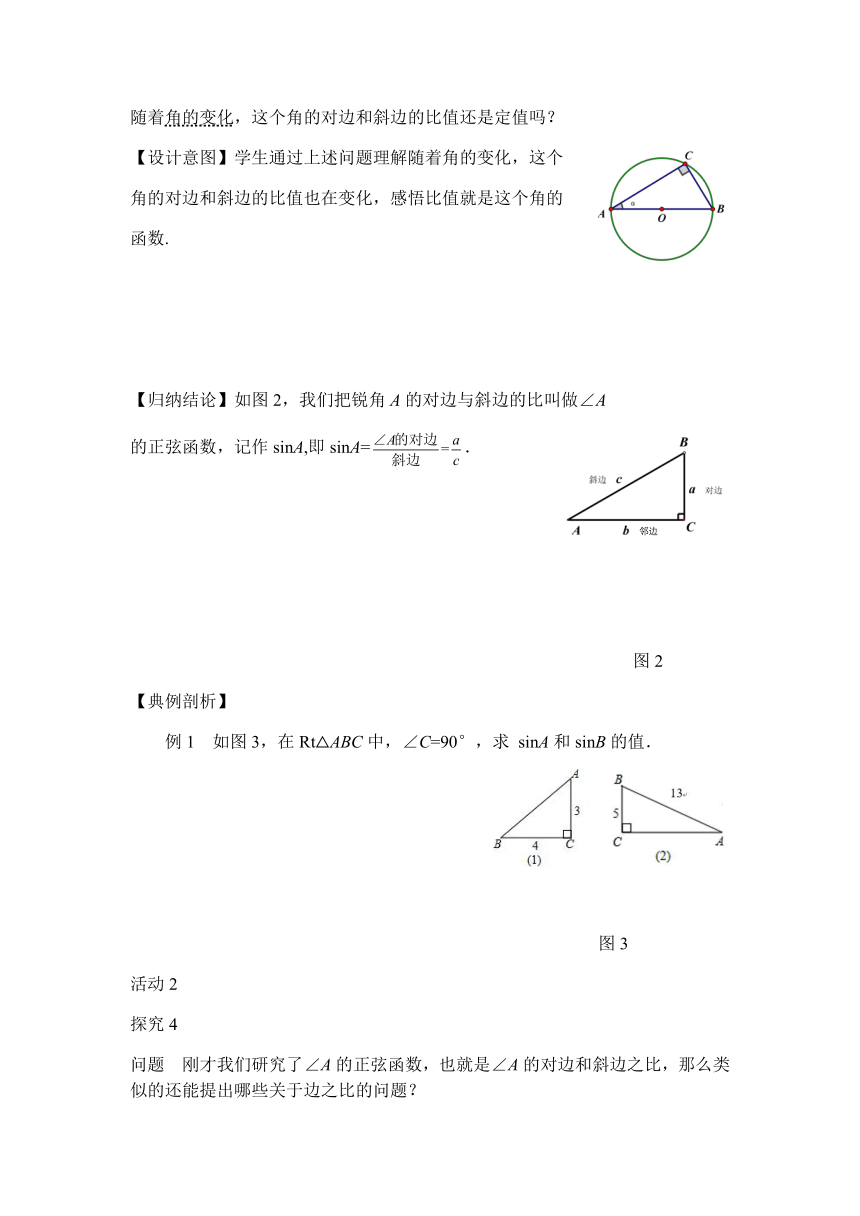
问题 如果将上述问题中的斜坡与水平面所成角的度数改成变化的角度α,那么随着角的变化,这个角的对边和斜边的比值还是定值吗?
【设计意图】学生通过上述问题理解随着角的变化,这个
角的对边和斜边的比值也在变化,感悟比值就是这个角的
函数.
【归纳结论】如图2,我们把锐角A的对边与斜边的比叫做∠A
的正弦函数,记作sinA,即sinA=.
图2
【典例剖析】
例1 如图3,在Rt△ABC中,∠C=90°,求 sinA和sinB的值.
图3
活动2
探究4
问题 刚才我们研究了∠A的正弦函数,也就是∠A的对边和斜边之比,那么类似的还能提出哪些关于边之比的问题?
【设计意图】类比已经学过的知识,学生通过思考,自主建构,可能会提出邻边与斜边、对边与邻边、斜边与邻边、邻边与对边之比等各位结论,引导学生建构余弦、正切函数.
【归纳结论】我们把锐角A的邻边与斜边的比叫做∠A的余弦函数,记作cosA,即cosA=,我们把锐角A的对边与邻边的比叫做∠A的正切函数,记作tanA,即tanA=,初中阶段我们只研究这3个函数,这里sinA, cosA, tanA都是一个完整的符号,单独的“sin”没有意义.其中A前面的 “∠”一般省略不写.∠A的正弦、余弦、正切都是∠A的锐角三角函数.
探究5
问题 根据图形,能得出这三个三角函数的取值范围吗?
【设计意图】通过取值范围的探究,学生会更注重数形结合,能够加深对这三个函数的理解,有利于建立角与边之间的关系.
【归纳结论】0
活动3
自主整理30°,45°,60°的三角函数值,小组交流结论,并提出猜想.
【设计意图】学生自主探究特殊角的三角函数值,进一步增加对三角函数的理解,同时为后续利用特殊角的三角函数值解决问题打下基础.
【归纳结论】
特殊角的三角函数值
三角函数 30° 45° 60°
sinA
cosA
tanA 1
除此之外还可能生成很多结论,比较重要的如:sinA= cos(90°-A),cosA=sin(90°-A), tanA×tan(90°-A)=1,sin2A+cos2A=1等结论.
【典例剖析】
例2 (1)求sin45°cos60°-cos45°;
(2)在Rt△ABC中,∠C=90°,AC=12,,求AB的长及sinB,cosA和tanA.
【设计意图】所选例题,可由学生自主探究完成.学生既能独立思考,又可相互合作,师生共同寻求解题方法,完成解答过程.本题学生先画图,利用图形的直观性来获得结论更好些.
【归纳结论】(2)利用参数思想,学生可以具体化对应边长,最终容易得出结论。
解:,设,则,,,
解得:或(舍,,,,,
.
三、运用新知
1. 如图4,在Rt△ABC中,是斜边上的高,,
则下列比值中不等于的是
A. B. C. D. 图4
2.求下列各式的值:
(1)cos260°+sin260°;
(2).
3.如图5,一块平行四边的木板两条邻边的长分别为
20cm和10cm,它们之间的夹角的正弦值为,求
这块木板的面积. 图5
【设计意图】巩固已经学习的知识点,进一步增加其数学活动经验.
【答案】1. D 2. (1)1,(2)0 3. 120cm2
四、归纳总结
学生小结本节课学到的知识点,教师帮助完善.
五、板书设计
【教学说明】
相对于其他函数而言,锐角三角函数难度加大,主要是因为其他函数是以某一个实数作为自变量,并不是所有的函数都可以用象限图表示,而锐角三角函数是以角度作为自变量,每个种类的三角函数都可画出相应的象限图,并且有一定的规律可循。但是锐角三角函数这一章节的内容较为复杂,对于学生而言一时难以辨认三角函数的种类及算法,若老师在课堂上运用的教学方法不当,会严重影响学生学习效果,因此,老师在正式上课前必须做好教学设计工作,结合实际情况完善教学方法.采用从实际问题中抽象出研究问题的方式,能体现抽象能力、 模型化能力,能使学生感悟研究锐角三角函数的意义.按 “锐角的正弦—锐 角的余弦、正切—锐角三角函数”的教学顺序展开,并把教学的侧重点放在锐角的 正弦函数上,显得比较自然,贴近学生的最近发展区,有利于学生自主建构.
邻边
