2019秋八年级数学上册13.2.5三角形全等的判定6斜边直角边课件(12张ppt)华东师大版
文档属性
| 名称 | 2019秋八年级数学上册13.2.5三角形全等的判定6斜边直角边课件(12张ppt)华东师大版 |  | |
| 格式 | zip | ||
| 文件大小 | 569.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 15:17:07 | ||
图片预览




文档简介
(共12张PPT)
13.2 三角形全等的判定
第13章 全等三角形
导入新课
讲授新课
当堂练习
课堂小结
6.斜边直角边
1.已知斜边、直角边会画直角三角形,经历画直角三角形探究
得到“H.L.”定理,体会“H.L.”的合理性.(重点)
2.掌握“H.L.”定理,能正确应用“H.L.”定理证明两个三角形全
等.(难点)
3.能正确应用所学的全等三角形的判定定理解决问题.(难点)
学习目标
导入新课
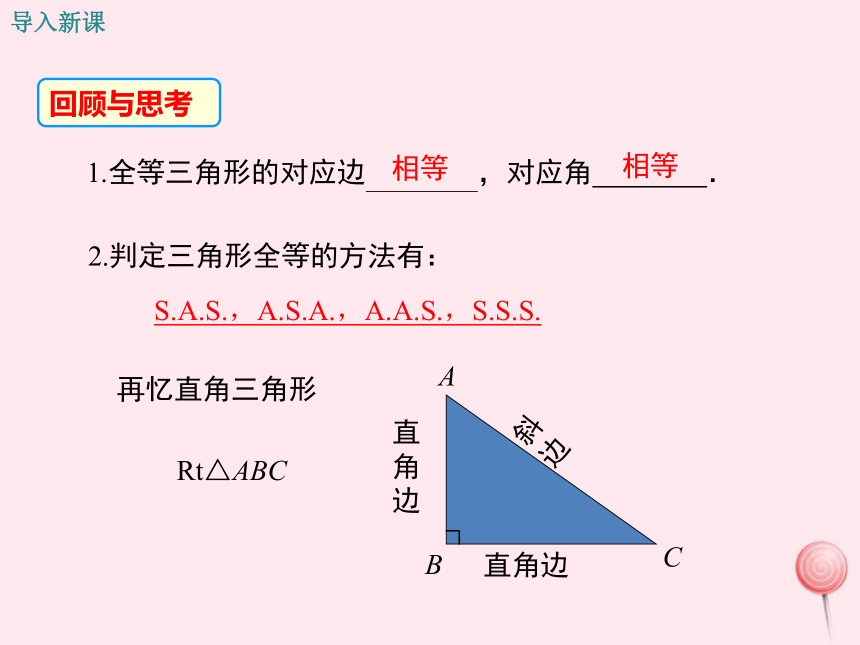
回顾与思考
1.全等三角形的对应边 ,对应角 .
相等
相等
2.判定三角形全等的方法有:
S.A.S.,A.S.A.,A.A.S.,S.S.S.
再忆直角三角形
Rt△ABC
直角边
斜边
A
B
C
直角边
讲授新课
舞台背景的形状是两个直角三角形,工作人员想知道两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住,无法测量.
(1) 你能帮他想个办法吗?
根据“S.A.S.”可测量其余两边与这两边的夹角.
根据“A.S.A.”,“A.A.S.”可测量对应一边和一锐角.
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等.于是,他就肯定“两个直角三角形是全等的”.
你相信这个结论吗?
(2)如果他只带一个卷尺,能完成这个任务吗?
下面,让我们来验证这个结论.
斜边和一条直角边对应相等→两个直角三角形全等?.
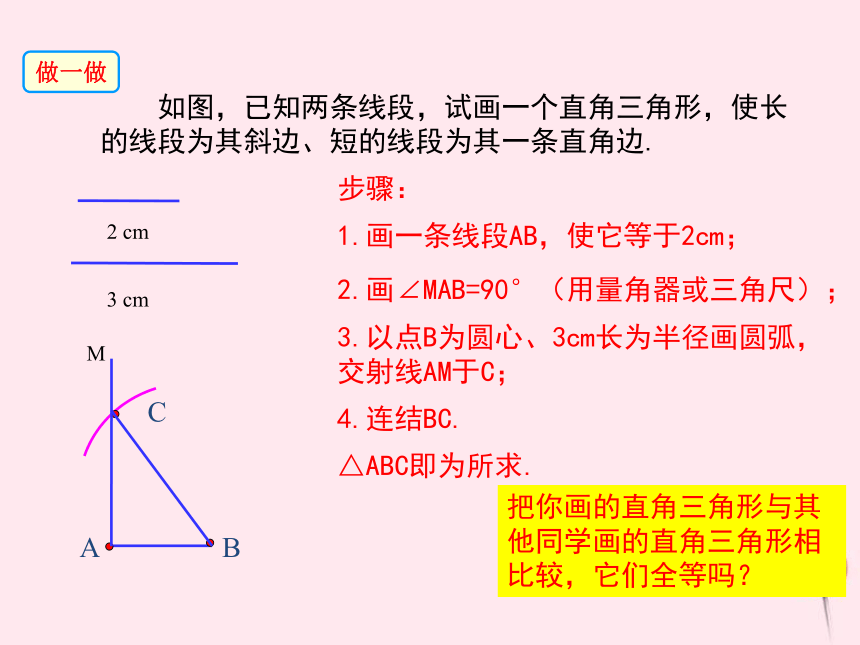
2 cm
3 cm
步骤:
1.画一条线段AB,使它等于2cm;
2.画∠MAB=90°(用量角器或三角尺);
3.以点B为圆心、3cm长为半径画圆弧,交射线AM于C;
△ABC即为所求.
把你画的直角三角形与其他同学画的直角三角形相比较,它们全等吗?
做一做
如图,已知两条线段,试画一个直角三角形,使长的线段为其斜边、短的线段为其一条直角边.
4.连结BC.
“斜边直角边”判定方法
文字语言:
斜边和一条直角边分别相等的两个直角三角形全等
(简写成“斜边直角边”或“H.L.”).
几何语言:
∴在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (H.L.).
∵∠C=∠C′=90°,
例 如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD.
证明: ∵ AC⊥BC, BD⊥AD,
∴∠C与∠D都是直角.
在 Rt△ABC 和Rt△BAD 中,
∴ Rt△ABC≌Rt△BAD (H.L.).
∴ BC﹦AD(全等三角形的对应边相等).
典例精析
当堂练习
1. 如图,∠B=∠D=90°,要证明△ABC 与△ADC全等,
还需要补充的条件是 (写出一个即可).
答案: AB=AD 或 BC=DC 或
∠BAC=∠DAC 或 ∠ACB=∠ACD
C
2.如图,在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE.求证:△EBC≌△DCB.
证明: ∵ BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中,
∴ Rt△EBC≌Rt△DCB (H.L.).
3.如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:BF=DE.
证明: ∵ BF⊥AC,DE⊥AC, ∴∠BFA=∠DEC=90 °.
∵AE=CF, ∴AE+EF=CF+EF,
即AF=CE.
在Rt△ABF和Rt△CDE中,
∴ Rt△ABF≌Rt△CDE(H.L.).
课堂小结
“斜边直角边”
内容
斜边和一条直角边分别相等的两个直角三角形全等.
前提条件
在直角三角形中
使用方法
只须找除直角外的两个条件即可
(两个条件中至少有一个条件是一组对应边相等)
13.2 三角形全等的判定
第13章 全等三角形
导入新课
讲授新课
当堂练习
课堂小结
6.斜边直角边
1.已知斜边、直角边会画直角三角形,经历画直角三角形探究
得到“H.L.”定理,体会“H.L.”的合理性.(重点)
2.掌握“H.L.”定理,能正确应用“H.L.”定理证明两个三角形全
等.(难点)
3.能正确应用所学的全等三角形的判定定理解决问题.(难点)
学习目标
导入新课
回顾与思考
1.全等三角形的对应边 ,对应角 .
相等
相等
2.判定三角形全等的方法有:
S.A.S.,A.S.A.,A.A.S.,S.S.S.
再忆直角三角形
Rt△ABC
直角边
斜边
A
B
C
直角边
讲授新课
舞台背景的形状是两个直角三角形,工作人员想知道两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住,无法测量.
(1) 你能帮他想个办法吗?
根据“S.A.S.”可测量其余两边与这两边的夹角.
根据“A.S.A.”,“A.A.S.”可测量对应一边和一锐角.
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等.于是,他就肯定“两个直角三角形是全等的”.
你相信这个结论吗?
(2)如果他只带一个卷尺,能完成这个任务吗?
下面,让我们来验证这个结论.
斜边和一条直角边对应相等→两个直角三角形全等?.
2 cm
3 cm
步骤:
1.画一条线段AB,使它等于2cm;
2.画∠MAB=90°(用量角器或三角尺);
3.以点B为圆心、3cm长为半径画圆弧,交射线AM于C;
△ABC即为所求.
把你画的直角三角形与其他同学画的直角三角形相比较,它们全等吗?
做一做
如图,已知两条线段,试画一个直角三角形,使长的线段为其斜边、短的线段为其一条直角边.
4.连结BC.
“斜边直角边”判定方法
文字语言:
斜边和一条直角边分别相等的两个直角三角形全等
(简写成“斜边直角边”或“H.L.”).
几何语言:
∴在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (H.L.).
∵∠C=∠C′=90°,
例 如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD.
证明: ∵ AC⊥BC, BD⊥AD,
∴∠C与∠D都是直角.
在 Rt△ABC 和Rt△BAD 中,
∴ Rt△ABC≌Rt△BAD (H.L.).
∴ BC﹦AD(全等三角形的对应边相等).
典例精析
当堂练习
1. 如图,∠B=∠D=90°,要证明△ABC 与△ADC全等,
还需要补充的条件是 (写出一个即可).
答案: AB=AD 或 BC=DC 或
∠BAC=∠DAC 或 ∠ACB=∠ACD
C
2.如图,在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE.求证:△EBC≌△DCB.
证明: ∵ BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中,
∴ Rt△EBC≌Rt△DCB (H.L.).
3.如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:BF=DE.
证明: ∵ BF⊥AC,DE⊥AC, ∴∠BFA=∠DEC=90 °.
∵AE=CF, ∴AE+EF=CF+EF,
即AF=CE.
在Rt△ABF和Rt△CDE中,
∴ Rt△ABF≌Rt△CDE(H.L.).
课堂小结
“斜边直角边”
内容
斜边和一条直角边分别相等的两个直角三角形全等.
前提条件
在直角三角形中
使用方法
只须找除直角外的两个条件即可
(两个条件中至少有一个条件是一组对应边相等)
