6.3 实数 课件
图片预览






文档简介
(共22张PPT)
人教版 初中数学
第五章 相交线与平行线
6.3 实数
问题引入
把有理数 写成小数的形式,它们有什么特征?
发现上面的分数都可以写成有限小数或者无限循环小数的形式。
问题引入
归纳:任何一个有理数(整数或分数)都可以写成有限小数或者无限循环小数的形式,反过来,任何有限小数或者无限循环小数也都是有理数。
探究新知
我们学过的数是否都具有问题1中数的特征?请举例说明.
一、无理数的概念
探究新知
思考: 是无理数吗?1.010 010 001 000 01…是无
理数吗?
1.01001000100001…
(1)含 的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001…
二、常见的无理数的三种形式
探究新知
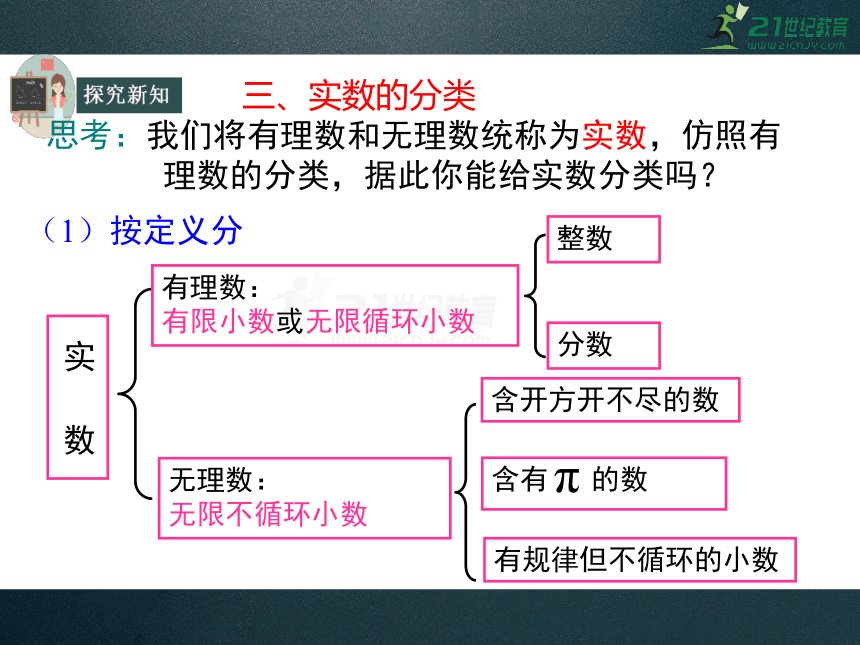
思考:我们将有理数和无理数统称为实数,仿照有
理数的分类,据此你能给实数分类吗?
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
(1)按定义分
分数
整数
含开方开不尽的数
有规律但不循环的小数
含有 的数
三、实数的分类
探究新知
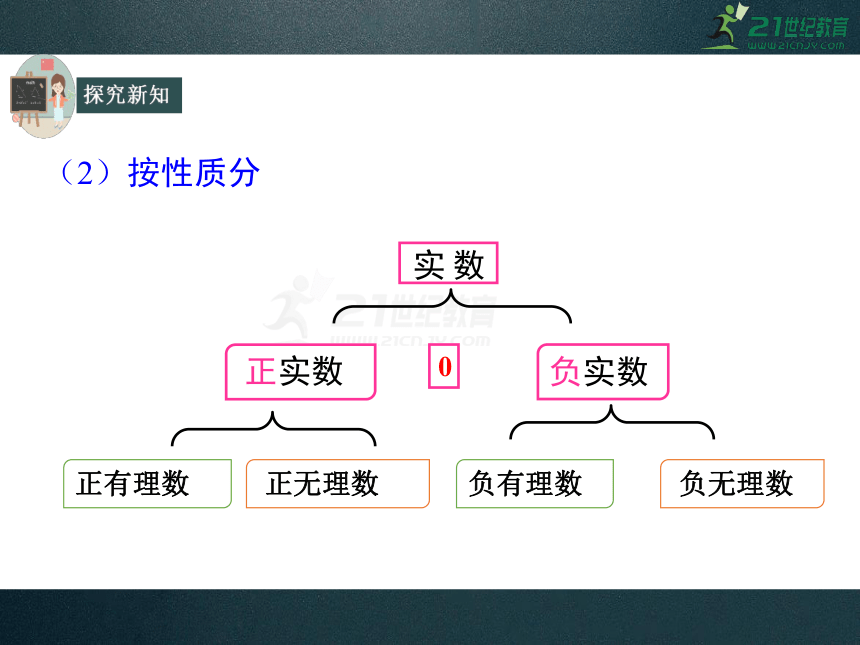
负实数
正实数
数实
正有理数
负有理数
(2)按性质分
0
正无理数
负无理数
探究新知
无理数:
有理数:
负实数:
正实数:
将下列各数分别填入下列相应的括号内:
注意:对每个数都要进行判断,分类标准不同结果不同。
探究新知
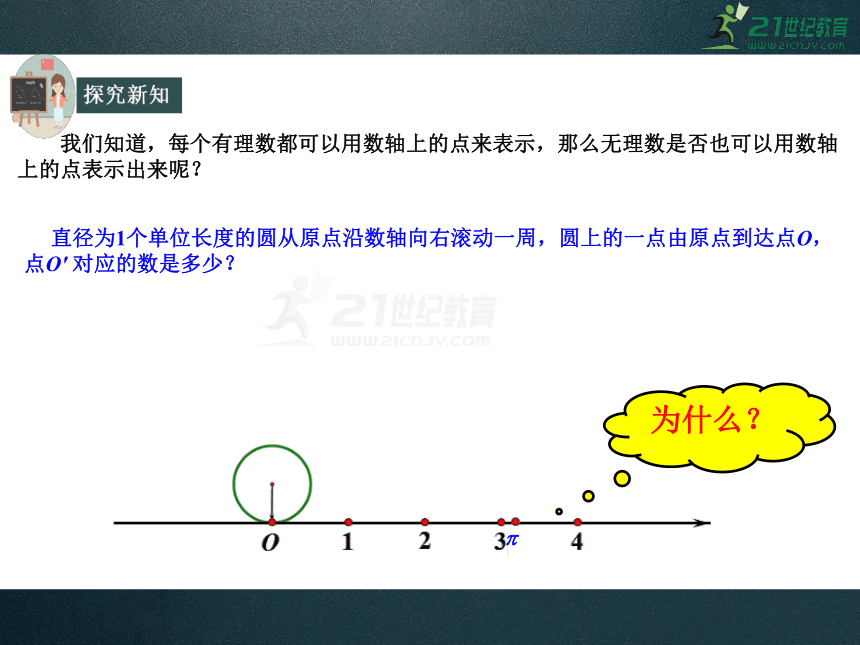
我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?
直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O,点O' 对应的数是多少?
p
为什么?
探究新知
我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?
直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O,点O' 对应的数是多少?
p
为什么?
探究新知
能否用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形?
小正方形对角线的长为_______dm。
探究新知
你能在数轴上找到表示 和 的点吗?
以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正半轴的交点表示什么?与负半轴的交点表示什么?
答:与正半轴的交点表示 ,
与负半轴的交点表示 。
每一个无理数都可以用数轴上的一个点表示出来.
实数与数轴上的点是一一对应的关系.
数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大。
探究新知
有理数关于相反数、绝对值的意义同样适合于实数
你能解答下列问题吗?
(1) 的相反数是______,-p 的相反数是______,
0 的相反数是______ ;
(2) = ____ ,|-p | = ____ ,| 0 | = ____ 。
p
0
p
0
实数a的相反数是-a
一个正实数的绝对值是它本身;一个负实数的绝对值是它的相反数; 0的绝对值是0.
练一练
(1) 的相反数是___; 的相反数是_______;
(2)____的相反数是 ; _____的相反数是 ;
(3) 的值是________;绝对值是________;
(4)一个数的绝对值是 ,那么这个数是________。
填空:
探究新知
有理数运算法则及运算性质同样适合于实数的运算.
1.计算下列各式的值:
(1) (2)
解:(1)
加法结合律
分配律
(2)
探究新知
2. 计算(结果保留小数点后两位):
解:(1)
(2)
随堂训练
1.下列说法正确的是( )
A.b一定是正实数
B. 是有理数
C. 是有理数
D.数轴上任一点都对应一个有理数
B
随堂训练
2.判断。
(1)实数不是有理数就是无理数。 ( )
(2)无理数都是无限不循环小数。 ( )
(4)无理数都是无限小数。 ( )
(3)带根号的数都是无理数。 ( )
(5)无理数一定都带根号。 ( )
×
×
随堂训练
3.计算
(1)
(2)
拓展延伸
计算
=4
课堂小结
今天我们学习了哪些知识?
1、举例说明有理数和无理数的特点是什么?
2、实数是由哪些数组成的?
3、实数与数轴上的点有什么关系?
4、什么是实数的相反数和绝对值?
https://www.21cnjy.com/help/help_extract.php
人教版 初中数学
第五章 相交线与平行线
6.3 实数
问题引入
把有理数 写成小数的形式,它们有什么特征?
发现上面的分数都可以写成有限小数或者无限循环小数的形式。
问题引入
归纳:任何一个有理数(整数或分数)都可以写成有限小数或者无限循环小数的形式,反过来,任何有限小数或者无限循环小数也都是有理数。
探究新知
我们学过的数是否都具有问题1中数的特征?请举例说明.
一、无理数的概念
探究新知
思考: 是无理数吗?1.010 010 001 000 01…是无
理数吗?
1.01001000100001…
(1)含 的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001…
二、常见的无理数的三种形式
探究新知
思考:我们将有理数和无理数统称为实数,仿照有
理数的分类,据此你能给实数分类吗?
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
(1)按定义分
分数
整数
含开方开不尽的数
有规律但不循环的小数
含有 的数
三、实数的分类
探究新知
负实数
正实数
数实
正有理数
负有理数
(2)按性质分
0
正无理数
负无理数
探究新知
无理数:
有理数:
负实数:
正实数:
将下列各数分别填入下列相应的括号内:
注意:对每个数都要进行判断,分类标准不同结果不同。
探究新知
我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?
直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O,点O' 对应的数是多少?
p
为什么?
探究新知
我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?
直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O,点O' 对应的数是多少?
p
为什么?
探究新知
能否用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形?
小正方形对角线的长为_______dm。
探究新知
你能在数轴上找到表示 和 的点吗?
以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正半轴的交点表示什么?与负半轴的交点表示什么?
答:与正半轴的交点表示 ,
与负半轴的交点表示 。
每一个无理数都可以用数轴上的一个点表示出来.
实数与数轴上的点是一一对应的关系.
数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大。
探究新知
有理数关于相反数、绝对值的意义同样适合于实数
你能解答下列问题吗?
(1) 的相反数是______,-p 的相反数是______,
0 的相反数是______ ;
(2) = ____ ,|-p | = ____ ,| 0 | = ____ 。
p
0
p
0
实数a的相反数是-a
一个正实数的绝对值是它本身;一个负实数的绝对值是它的相反数; 0的绝对值是0.
练一练
(1) 的相反数是___; 的相反数是_______;
(2)____的相反数是 ; _____的相反数是 ;
(3) 的值是________;绝对值是________;
(4)一个数的绝对值是 ,那么这个数是________。
填空:
探究新知
有理数运算法则及运算性质同样适合于实数的运算.
1.计算下列各式的值:
(1) (2)
解:(1)
加法结合律
分配律
(2)
探究新知
2. 计算(结果保留小数点后两位):
解:(1)
(2)
随堂训练
1.下列说法正确的是( )
A.b一定是正实数
B. 是有理数
C. 是有理数
D.数轴上任一点都对应一个有理数
B
随堂训练
2.判断。
(1)实数不是有理数就是无理数。 ( )
(2)无理数都是无限不循环小数。 ( )
(4)无理数都是无限小数。 ( )
(3)带根号的数都是无理数。 ( )
(5)无理数一定都带根号。 ( )
×
×
随堂训练
3.计算
(1)
(2)
拓展延伸
计算
=4
课堂小结
今天我们学习了哪些知识?
1、举例说明有理数和无理数的特点是什么?
2、实数是由哪些数组成的?
3、实数与数轴上的点有什么关系?
4、什么是实数的相反数和绝对值?
https://www.21cnjy.com/help/help_extract.php
