人教版八年级上数学教学讲义,复习补习资料(巩固练习):58【提高】《分式》全章复习与巩固含答案
文档属性
| 名称 | 人教版八年级上数学教学讲义,复习补习资料(巩固练习):58【提高】《分式》全章复习与巩固含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 128.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-10 00:00:00 | ||
图片预览



文档简介
分式全章复习与巩固(提高)
【学习目标】
1. 理解分式的概念,能求出使分式有意义、分式无意义、分式值为0的条件.
2.了解分式的基本性质,掌握分式的约分和通分法则.
3.掌握分式的四则运算.
4.结合分式的运算,将指数的讨论范围从正整数扩大到全体整数,构建和发展相互联系的 知识体系.
5.结合分析和解决实际问题,讨论可以化为一元一次方程的分式方程,掌握这种方程的解法,体会解方程中的化归思想.
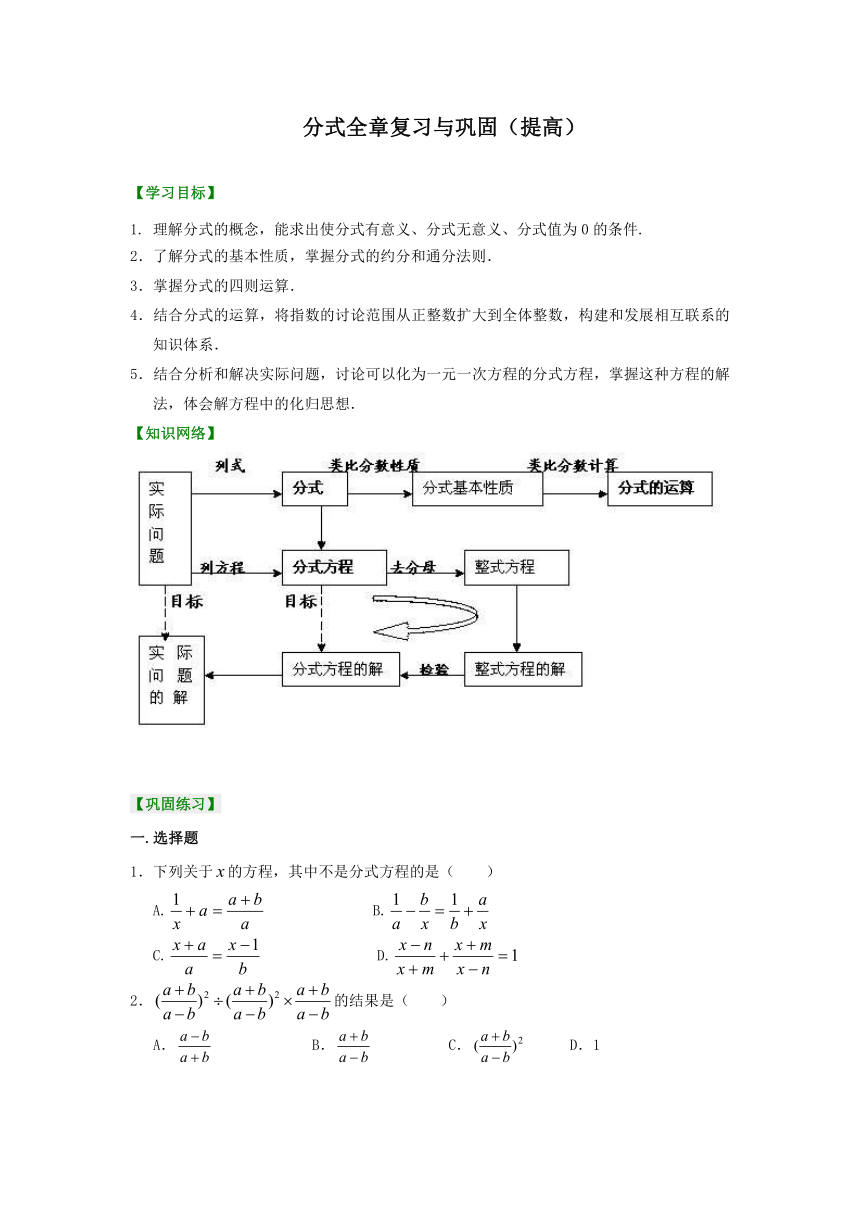
【知识网络】
【巩固练习】
一.选择题
1.下列关于的方程,其中不是分式方程的是( )
A. B.
C. D.
2.的结果是( )
A. B. C. D.1
3.分式方程的解是( )
A.0 B.2 C.0或2 D.无解
4.(2019?周口校级一模)若关于x的分式方程有增根,则m的值是( )
A.m=﹣1 B.m=2 C.m=3 D.m=0或m=3
5.某农场挖一条480米的渠道,开工后,每天比原计划多挖20米,结果提前4天完成任务,若设原计划每天挖米,那么下列方程正确的是( )
A. B.
C. D.
6.化简的结果是( ).
A. B. C. D.
7.若关于的方程有增根,则的值为( ).
A.13 B.-11 C.9 D.3
8. 甲、乙两人分别从两地同时出发,若相向而行,则经过相遇;若同向而行,则经过 甲追上乙.那么甲的速度是乙的( )
A.倍 B.倍 C.倍 D.倍
二.填空题
9.若分式的值为0,则的值为______.
10.若,且>0,则分式的值为______.
11.化简______;=______.
12.______.
13.(2019春?成都期末)计算:= _____(结果化为只含正整数指数幂的形式).
14.(沧浪区校级期中)已知,则= .
15.若分式方程的解是,则______.
16.个人天可做个零件(设每人速度一样),则个人用同样速度做个零件所需天数是________.
三.解答题
17.(1)已知,求,的值;
(2)已知,求的值.
18.(北京校级期中)已知x2﹣x﹣6=0,求的值.
19.为何值时,关于的方程会产生增根?
20. 某文化用品商店用2000元购进一批学生书包,上市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
【答案与解析】
一.选择题
1. 【答案】C;
【解析】分式方程是分母含有未知数的等式.
2. 【答案】B;
【解析】.
3. 【答案】D;
【解析】去分母得,,解得是增根.
4. 【答案】C;
【解析】解:分式方程去分母得:,
由分式方程有增根,得到,即,
把代入整式方程得:.
故选C.
5. 【答案】A;
【解析】原计划所用时间为,实际所用时间为,选A.
6. 【答案】B;
【解析】.
7. 【答案】D;
【解析】因为所给的关于的方程有增根,即有,所以增根是.而 一定是整式方程的根,将其代入得,所以.
8. 【答案】C;
【解析】不妨设甲乙两人开始时相距s千米,甲的速度为,乙的速度为,
则根据题意有于是 ,
所以 ,即.甲的速度是乙的倍.
二.填空题
9. 【答案】0;
【解析】由题意且,解得.
10.【答案】1;
【解析】由得,因为>0,所以,代入原式得.
11.【答案】;;
【解析】;.
12.【答案】4;
【解析】.
13.【答案】;
【解析】.
14.【答案】;
【解析】解:设=k,则x=2k,y=3k,z=4k,则===.
15.【答案】7;
【解析】将代入原方程,解得.
16.【答案】;
【解析】每人每天做个零件,个人用同样速度做个零件所需天数是
.
三.解答题
17.【解析】
解:(1)因为,所以,
所以,所以.
所以.同理可得.
(2)因为,所以,
所以,所以.
18.【解析】
解:∵x2﹣x﹣6=0,
∴x2=x+6,
∴把x2=x+6代入:
原式=
=
=
=
=
=
所以原式的值是.
19.【解析】
解:方程两边都乘以,得.
整理得.
当时,方程无解.
当时,.
如果方程有增根,那么,即,或.
当时,,所以;
当时,,所以.
所以当或时,原方程会产生增根.
20.【解析】
解:(1)设第一批购进书包的单价为元,则第二批购进书包的单价为元,第一批购进书包个,第二批购进书包个.
依题意,得,
整理,得,解得.经检验是原方程的根.
(2)(元).
答:第一批购进书包的单价为80元.商店共盈利3700元.
【学习目标】
1. 理解分式的概念,能求出使分式有意义、分式无意义、分式值为0的条件.
2.了解分式的基本性质,掌握分式的约分和通分法则.
3.掌握分式的四则运算.
4.结合分式的运算,将指数的讨论范围从正整数扩大到全体整数,构建和发展相互联系的 知识体系.
5.结合分析和解决实际问题,讨论可以化为一元一次方程的分式方程,掌握这种方程的解法,体会解方程中的化归思想.
【知识网络】
【巩固练习】
一.选择题
1.下列关于的方程,其中不是分式方程的是( )
A. B.
C. D.
2.的结果是( )
A. B. C. D.1
3.分式方程的解是( )
A.0 B.2 C.0或2 D.无解
4.(2019?周口校级一模)若关于x的分式方程有增根,则m的值是( )
A.m=﹣1 B.m=2 C.m=3 D.m=0或m=3
5.某农场挖一条480米的渠道,开工后,每天比原计划多挖20米,结果提前4天完成任务,若设原计划每天挖米,那么下列方程正确的是( )
A. B.
C. D.
6.化简的结果是( ).
A. B. C. D.
7.若关于的方程有增根,则的值为( ).
A.13 B.-11 C.9 D.3
8. 甲、乙两人分别从两地同时出发,若相向而行,则经过相遇;若同向而行,则经过 甲追上乙.那么甲的速度是乙的( )
A.倍 B.倍 C.倍 D.倍
二.填空题
9.若分式的值为0,则的值为______.
10.若,且>0,则分式的值为______.
11.化简______;=______.
12.______.
13.(2019春?成都期末)计算:= _____(结果化为只含正整数指数幂的形式).
14.(沧浪区校级期中)已知,则= .
15.若分式方程的解是,则______.
16.个人天可做个零件(设每人速度一样),则个人用同样速度做个零件所需天数是________.
三.解答题
17.(1)已知,求,的值;
(2)已知,求的值.
18.(北京校级期中)已知x2﹣x﹣6=0,求的值.
19.为何值时,关于的方程会产生增根?
20. 某文化用品商店用2000元购进一批学生书包,上市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
【答案与解析】
一.选择题
1. 【答案】C;
【解析】分式方程是分母含有未知数的等式.
2. 【答案】B;
【解析】.
3. 【答案】D;
【解析】去分母得,,解得是增根.
4. 【答案】C;
【解析】解:分式方程去分母得:,
由分式方程有增根,得到,即,
把代入整式方程得:.
故选C.
5. 【答案】A;
【解析】原计划所用时间为,实际所用时间为,选A.
6. 【答案】B;
【解析】.
7. 【答案】D;
【解析】因为所给的关于的方程有增根,即有,所以增根是.而 一定是整式方程的根,将其代入得,所以.
8. 【答案】C;
【解析】不妨设甲乙两人开始时相距s千米,甲的速度为,乙的速度为,
则根据题意有于是 ,
所以 ,即.甲的速度是乙的倍.
二.填空题
9. 【答案】0;
【解析】由题意且,解得.
10.【答案】1;
【解析】由得,因为>0,所以,代入原式得.
11.【答案】;;
【解析】;.
12.【答案】4;
【解析】.
13.【答案】;
【解析】.
14.【答案】;
【解析】解:设=k,则x=2k,y=3k,z=4k,则===.
15.【答案】7;
【解析】将代入原方程,解得.
16.【答案】;
【解析】每人每天做个零件,个人用同样速度做个零件所需天数是
.
三.解答题
17.【解析】
解:(1)因为,所以,
所以,所以.
所以.同理可得.
(2)因为,所以,
所以,所以.
18.【解析】
解:∵x2﹣x﹣6=0,
∴x2=x+6,
∴把x2=x+6代入:
原式=
=
=
=
=
=
所以原式的值是.
19.【解析】
解:方程两边都乘以,得.
整理得.
当时,方程无解.
当时,.
如果方程有增根,那么,即,或.
当时,,所以;
当时,,所以.
所以当或时,原方程会产生增根.
20.【解析】
解:(1)设第一批购进书包的单价为元,则第二批购进书包的单价为元,第一批购进书包个,第二批购进书包个.
依题意,得,
整理,得,解得.经检验是原方程的根.
(2)(元).
答:第一批购进书包的单价为80元.商店共盈利3700元.
