人教版八年级数学上册课件:11.2.2 三角形的外角 (共19张PPT)
文档属性
| 名称 | 人教版八年级数学上册课件:11.2.2 三角形的外角 (共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 237.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-13 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
11.2 与三角形有关的角
11.2.2 三角形的外角
2 . 在△ABC中,
(1)∠C=90°,∠A=20 ° ,则∠B= ;
(2)∠A=40 ° ,∠B=∠C,则∠B= .
1 . 三角形三个内角的和等于多少度?
70°
70°
三角形的内角和等于180度
(一)知识回顾,温故知新
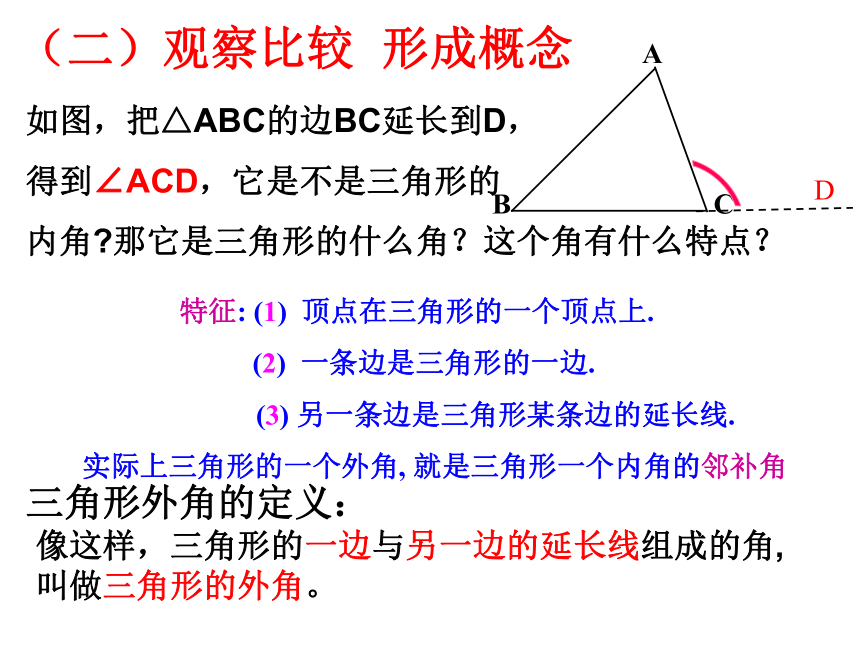
(二)观察比较 形成概念
A
B
C
三角形外角的定义:
如图,把△ABC的边BC延长到D,
得到∠ACD,它是不是三角形的
内角?那它是三角形的什么角?这个角有什么特点?
D
像这样,三角形的一边与另一边的延长线组成的角,
叫做三角形的外角。
特征: (1) 顶点在三角形的一个顶点上.
(2) 一条边是三角形的一边.
(3) 另一条边是三角形某条边的延长线.
实际上三角形的一个外角, 就是三角形一个内角的邻补角
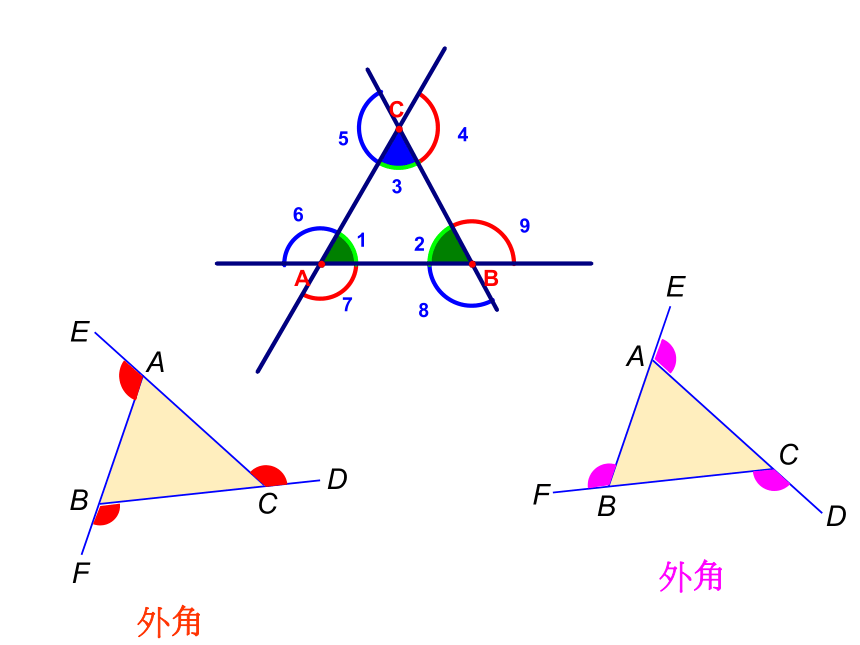
任意画一个三角形,再画出它所有的外角,请动手试一试。
想一想:
1.每一个三角形有几个外角?
2.每一个顶点处相对应的外角有几个?
3.这些外角中有几对外角相等?
4.三角形的每一个外角与三角形的三个内角有什么位置关系?
画图并思考
A
B
D
E
F
C
外角
A
B
D
E
F
C
外角
归纳:
1.每一个三角形都有____个外角;
2.每一个顶点相对应的外角都有___个。
4.一个三角形的每一个外角对应一个
_____________和两个______________.
3.这6个外角中有_____对外角相等。
6
2
3
相邻的内角
不相邻的内角
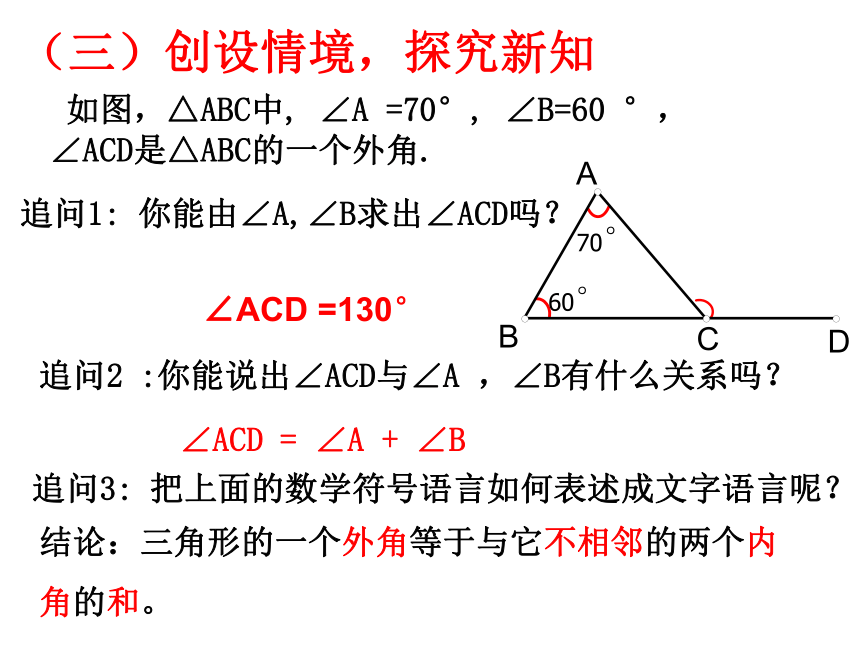
(三)创设情境,探究新知
如图,△ABC中, ∠A =70°, ∠B=60 °,
∠ACD是△ABC的一个外角.
70°
60°
追问1: 你能由∠A,∠B求出∠ACD吗?
∠ACD =130°
追问2 :你能说出∠ACD与∠A ,∠B有什么关系吗?
∠ACD = ∠A + ∠B
追问3: 把上面的数学符号语言如何表述成文字语言呢?
结论:三角形的一个外角等于与它不相邻的两个内
角的和。
通过上题的计算,任意一个三角形的外角与它不相邻的两个内角是否都有这种关系?请你试着去证明.
想一想:
已知 △ABC,∠ACD是△ABC的一个外角.
求证 ∠ACD = ∠A + ∠B
D
证明:过C作CE平行于AB
A
B
C
1
2
∴ ∠1= ∠B
(两直线平行,同位角相等)
∠2= ∠A
(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B
E
性质1 三角形的一个外角等于与它不相邻的两个内角的和
D
A
C
B
∵∠ACD= ∠A+ ∠B
∴∠ACD﹥∠A
∠ACD﹥ ∠B
在上图中,由加数与和的关系你还能知道什么?∠ACD大于∠A吗?大于∠B吗?
性质2 三角形的一个外角大于任何一个与
它不相邻的内角。
性质1、三角形的一个外角等于
与它不相邻的两个内角的
和。∠ACD =∠A+∠B
性质2、三角形的一个外角大于任何
一个与它不相邻的内角。
∠ACD > ∠A, ∠ACD > ∠B
A
C
B
D
三角形外角的性质:
A
B
C
1
2
3
解:
∵∠1=∠ABC+∠ACB,
∠2=∠BAC+∠ACB,
∠3=∠BAC+∠ABC,
∴∠1+∠2+∠3=2(∠ABC+∠BAC+∠ACB)
又∵ ∠ABC+∠BAC+∠ACB=1800
∴∠1+∠2+∠3=3600
结论:
三角形的外角和是3600。
例4.如图,∠1、∠2、∠3是△ABC的三个外角,
问∠1+∠2+∠3=?
(四) 解决问题,巩固新知
说一说 求出下列图形中∠1、∠2的度数。
(五)变式训练,拓展提升
(1) (2) (3)
(4)CE平分∠BCD
(5) (6)
(5)
(6)
(1)∠1=40°∠2=140°
(2)∠1=110°∠2=70°
(3)∠1=50°∠2=140°
(5)∠1=80°∠2=40°
(4)∠1=55°∠2=70°
(6)∠1=60°∠2=30°
判断题:
1.三角形的外角和是指三角形所有外角的和。( )
2.三角形的外角和等于它内角和的2倍。( )
3.三角形的一个外角等于两个内角的和。( )
4.三角形的一个外角等于与它不相邻的
两个内角的和。( )
5.三角形的一个外角大于任何一个内角。( )
6.三角形的一个内角小于任何一个与它
不相邻的外角。( )
把图中∠1、 ∠2、 ∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
练一练
通过这节课的学习,你有什么收获?
3.三角形的一个外角等于与它不相邻的两个内角的和。
三角形的一个外角大于与它不相邻的任何一个内角。
4.三角形的外角和为360°。
(六)回顾反思,分享收获
1.三角形的外角:
三角形的一边与另一边的延长线组成的角。
特征: (1) 顶点在三角形的一个顶点上;(2) 一条边是三角形的一边;(3)另一边是三角形某条边的延长线.
2.三角形的一个外角与它相邻的内角互补。
(七)分层作业,巩固提高
P17 习题11.2
必做题:第5、6题。
选做题:第11题.
谢谢
已知:国旗上的正五角星形如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
挑战自己
A
B
C
D
E
F
1
H
2
11.2 与三角形有关的角
11.2.2 三角形的外角
2 . 在△ABC中,
(1)∠C=90°,∠A=20 ° ,则∠B= ;
(2)∠A=40 ° ,∠B=∠C,则∠B= .
1 . 三角形三个内角的和等于多少度?
70°
70°
三角形的内角和等于180度
(一)知识回顾,温故知新
(二)观察比较 形成概念
A
B
C
三角形外角的定义:
如图,把△ABC的边BC延长到D,
得到∠ACD,它是不是三角形的
内角?那它是三角形的什么角?这个角有什么特点?
D
像这样,三角形的一边与另一边的延长线组成的角,
叫做三角形的外角。
特征: (1) 顶点在三角形的一个顶点上.
(2) 一条边是三角形的一边.
(3) 另一条边是三角形某条边的延长线.
实际上三角形的一个外角, 就是三角形一个内角的邻补角
任意画一个三角形,再画出它所有的外角,请动手试一试。
想一想:
1.每一个三角形有几个外角?
2.每一个顶点处相对应的外角有几个?
3.这些外角中有几对外角相等?
4.三角形的每一个外角与三角形的三个内角有什么位置关系?
画图并思考
A
B
D
E
F
C
外角
A
B
D
E
F
C
外角
归纳:
1.每一个三角形都有____个外角;
2.每一个顶点相对应的外角都有___个。
4.一个三角形的每一个外角对应一个
_____________和两个______________.
3.这6个外角中有_____对外角相等。
6
2
3
相邻的内角
不相邻的内角
(三)创设情境,探究新知
如图,△ABC中, ∠A =70°, ∠B=60 °,
∠ACD是△ABC的一个外角.
70°
60°
追问1: 你能由∠A,∠B求出∠ACD吗?
∠ACD =130°
追问2 :你能说出∠ACD与∠A ,∠B有什么关系吗?
∠ACD = ∠A + ∠B
追问3: 把上面的数学符号语言如何表述成文字语言呢?
结论:三角形的一个外角等于与它不相邻的两个内
角的和。
通过上题的计算,任意一个三角形的外角与它不相邻的两个内角是否都有这种关系?请你试着去证明.
想一想:
已知 △ABC,∠ACD是△ABC的一个外角.
求证 ∠ACD = ∠A + ∠B
D
证明:过C作CE平行于AB
A
B
C
1
2
∴ ∠1= ∠B
(两直线平行,同位角相等)
∠2= ∠A
(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B
E
性质1 三角形的一个外角等于与它不相邻的两个内角的和
D
A
C
B
∵∠ACD= ∠A+ ∠B
∴∠ACD﹥∠A
∠ACD﹥ ∠B
在上图中,由加数与和的关系你还能知道什么?∠ACD大于∠A吗?大于∠B吗?
性质2 三角形的一个外角大于任何一个与
它不相邻的内角。
性质1、三角形的一个外角等于
与它不相邻的两个内角的
和。∠ACD =∠A+∠B
性质2、三角形的一个外角大于任何
一个与它不相邻的内角。
∠ACD > ∠A, ∠ACD > ∠B
A
C
B
D
三角形外角的性质:
A
B
C
1
2
3
解:
∵∠1=∠ABC+∠ACB,
∠2=∠BAC+∠ACB,
∠3=∠BAC+∠ABC,
∴∠1+∠2+∠3=2(∠ABC+∠BAC+∠ACB)
又∵ ∠ABC+∠BAC+∠ACB=1800
∴∠1+∠2+∠3=3600
结论:
三角形的外角和是3600。
例4.如图,∠1、∠2、∠3是△ABC的三个外角,
问∠1+∠2+∠3=?
(四) 解决问题,巩固新知
说一说 求出下列图形中∠1、∠2的度数。
(五)变式训练,拓展提升
(1) (2) (3)
(4)CE平分∠BCD
(5) (6)
(5)
(6)
(1)∠1=40°∠2=140°
(2)∠1=110°∠2=70°
(3)∠1=50°∠2=140°
(5)∠1=80°∠2=40°
(4)∠1=55°∠2=70°
(6)∠1=60°∠2=30°
判断题:
1.三角形的外角和是指三角形所有外角的和。( )
2.三角形的外角和等于它内角和的2倍。( )
3.三角形的一个外角等于两个内角的和。( )
4.三角形的一个外角等于与它不相邻的
两个内角的和。( )
5.三角形的一个外角大于任何一个内角。( )
6.三角形的一个内角小于任何一个与它
不相邻的外角。( )
把图中∠1、 ∠2、 ∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
练一练
通过这节课的学习,你有什么收获?
3.三角形的一个外角等于与它不相邻的两个内角的和。
三角形的一个外角大于与它不相邻的任何一个内角。
4.三角形的外角和为360°。
(六)回顾反思,分享收获
1.三角形的外角:
三角形的一边与另一边的延长线组成的角。
特征: (1) 顶点在三角形的一个顶点上;(2) 一条边是三角形的一边;(3)另一边是三角形某条边的延长线.
2.三角形的一个外角与它相邻的内角互补。
(七)分层作业,巩固提高
P17 习题11.2
必做题:第5、6题。
选做题:第11题.
谢谢
已知:国旗上的正五角星形如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
挑战自己
A
B
C
D
E
F
1
H
2
