沪教版八上:19.10两点间的距离公式 教案
文档属性
| 名称 | 沪教版八上:19.10两点间的距离公式 教案 | 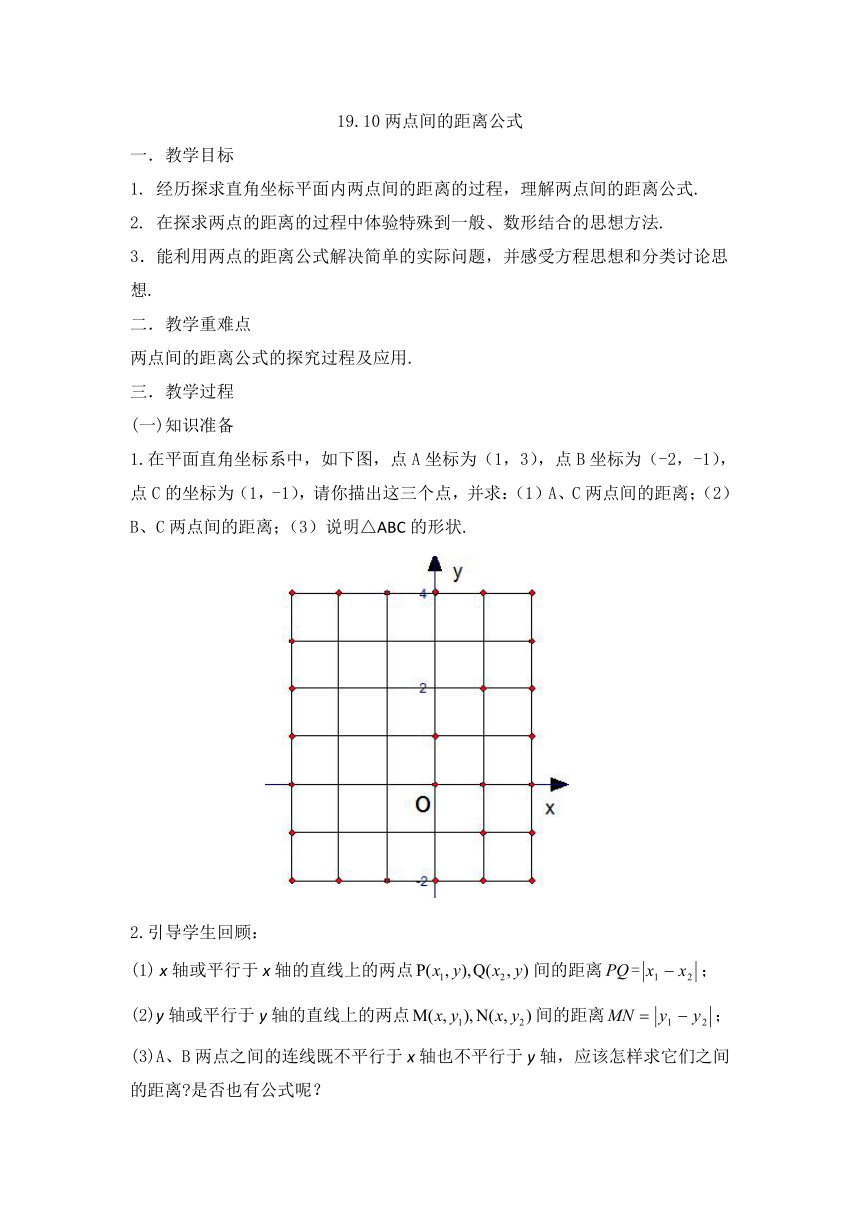 | |
| 格式 | zip | ||
| 文件大小 | 32.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 14:43:55 | ||
图片预览

文档简介
19.10两点间的距离公式
一.教学目标
1. 经历探求直角坐标平面内两点间的距离的过程,理解两点间的距离公式.
2. 在探求两点的距离的过程中体验特殊到一般、数形结合的思想方法.
3.能利用两点的距离公式解决简单的实际问题,并感受方程思想和分类讨论思想.
二.教学重难点
两点间的距离公式的探究过程及应用.
三.教学过程
(一)知识准备
1.在平面直角坐标系中,如下图,点A坐标为(1,3),点B坐标为(-2,-1),点C的坐标为(1,-1),请你描出这三个点,并求:(1)A、C两点间的距离;(2)B、C两点间的距离;(3)说明△ABC的形状.
2.引导学生回顾:
(1) x轴或平行于x轴的直线上的两点间的距离=;
(2)y轴或平行于y轴的直线上的两点间的距离;
(3)A、B两点之间的连线既不平行于x轴也不平行于y轴,应该怎样求它们之间的距离?是否也有公式呢?
【设计意图】:让学生复习特殊的两点之间的距离公式。通过感受三角形的形状,为后续构造直角三角形埋下伏笔.
(二)探索讨论
1.求(一)中的点A、B两点之间的距离.
【设计意图】让学生把AB放到直角三角形中运用勾股定理来求解,为一般情况下任意两点间距离(连线不与x轴、y轴平行)的计算时构造辅助线做铺垫.
2. 如果在直角坐标平面内有两点分别为A、B,那么A、B两点间的距离是多少呢?
=,
【设计意图】1.让学生在前面基础上互相讨论得出辅助线的作法,知道如何构造直角三角形;
2.对上述平行于y轴的线段AC、平行于x轴的线段BC的两点间距离公式与两点(它们的连线不与x轴、y轴平行)间距离公式统一性作说明。
(三)尝试解决
例题1:已知,直角坐标平面内,点A(-3,1), B(7,1), C(-1,-3),
(1)求下列两点间的距离:AB,AC,BC ; (2)判断△ABC的形状.
【设计意图】巩固公式的应用,并规范解题格式.
例题2:如图,在平面直角坐标系xOy中,点A(1,4),点B(5,1).
(1)求A、B两点间的距离;(2)在x轴上找一点M,使得△ABM是以AM为腰的等腰三角形,求出点M的坐标;(3)是否存在点P到A,B两点的距离相等,且到∠xOy的两边的距离相等.若有,点P的坐标为 .若没有,请说明理由.
【设计意图】体现方程、数形结合思想和分类讨论的方法。
(四)自我反馈
已知直角坐标平面内的两点A(3,0),B(6,4),
(1)点P在 轴上,且△PAB为等腰三角形,求点P的坐标。
(2)若△PAB为等边三角形,求点P的坐标。
【设计意图】1.等腰三角形的底和腰不确定时,可按任意选定一条边做底来分3类讨论;2.注意数形结合,问题(1)中用方程求解会出现三点共线的情况,需要从形上去检验。
(五)自我小结
让学生自己说,老师引导归纳梳理重要知识点、思想和方法。
(六)布置作业
1.书面作业:P134第1、2、3题
2.查找地理坐标在求两地距离上的应用方面的相关资料。
一.教学目标
1. 经历探求直角坐标平面内两点间的距离的过程,理解两点间的距离公式.
2. 在探求两点的距离的过程中体验特殊到一般、数形结合的思想方法.
3.能利用两点的距离公式解决简单的实际问题,并感受方程思想和分类讨论思想.
二.教学重难点
两点间的距离公式的探究过程及应用.
三.教学过程
(一)知识准备
1.在平面直角坐标系中,如下图,点A坐标为(1,3),点B坐标为(-2,-1),点C的坐标为(1,-1),请你描出这三个点,并求:(1)A、C两点间的距离;(2)B、C两点间的距离;(3)说明△ABC的形状.
2.引导学生回顾:
(1) x轴或平行于x轴的直线上的两点间的距离=;
(2)y轴或平行于y轴的直线上的两点间的距离;
(3)A、B两点之间的连线既不平行于x轴也不平行于y轴,应该怎样求它们之间的距离?是否也有公式呢?
【设计意图】:让学生复习特殊的两点之间的距离公式。通过感受三角形的形状,为后续构造直角三角形埋下伏笔.
(二)探索讨论
1.求(一)中的点A、B两点之间的距离.
【设计意图】让学生把AB放到直角三角形中运用勾股定理来求解,为一般情况下任意两点间距离(连线不与x轴、y轴平行)的计算时构造辅助线做铺垫.
2. 如果在直角坐标平面内有两点分别为A、B,那么A、B两点间的距离是多少呢?
=,
【设计意图】1.让学生在前面基础上互相讨论得出辅助线的作法,知道如何构造直角三角形;
2.对上述平行于y轴的线段AC、平行于x轴的线段BC的两点间距离公式与两点(它们的连线不与x轴、y轴平行)间距离公式统一性作说明。
(三)尝试解决
例题1:已知,直角坐标平面内,点A(-3,1), B(7,1), C(-1,-3),
(1)求下列两点间的距离:AB,AC,BC ; (2)判断△ABC的形状.
【设计意图】巩固公式的应用,并规范解题格式.
例题2:如图,在平面直角坐标系xOy中,点A(1,4),点B(5,1).
(1)求A、B两点间的距离;(2)在x轴上找一点M,使得△ABM是以AM为腰的等腰三角形,求出点M的坐标;(3)是否存在点P到A,B两点的距离相等,且到∠xOy的两边的距离相等.若有,点P的坐标为 .若没有,请说明理由.
【设计意图】体现方程、数形结合思想和分类讨论的方法。
(四)自我反馈
已知直角坐标平面内的两点A(3,0),B(6,4),
(1)点P在 轴上,且△PAB为等腰三角形,求点P的坐标。
(2)若△PAB为等边三角形,求点P的坐标。
【设计意图】1.等腰三角形的底和腰不确定时,可按任意选定一条边做底来分3类讨论;2.注意数形结合,问题(1)中用方程求解会出现三点共线的情况,需要从形上去检验。
(五)自我小结
让学生自己说,老师引导归纳梳理重要知识点、思想和方法。
(六)布置作业
1.书面作业:P134第1、2、3题
2.查找地理坐标在求两地距离上的应用方面的相关资料。
