沪教版八上:19.7 直角三角形全等的判定 课件(22张PPT)
文档属性
| 名称 | 沪教版八上:19.7 直角三角形全等的判定 课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 14:56:52 | ||
图片预览



文档简介
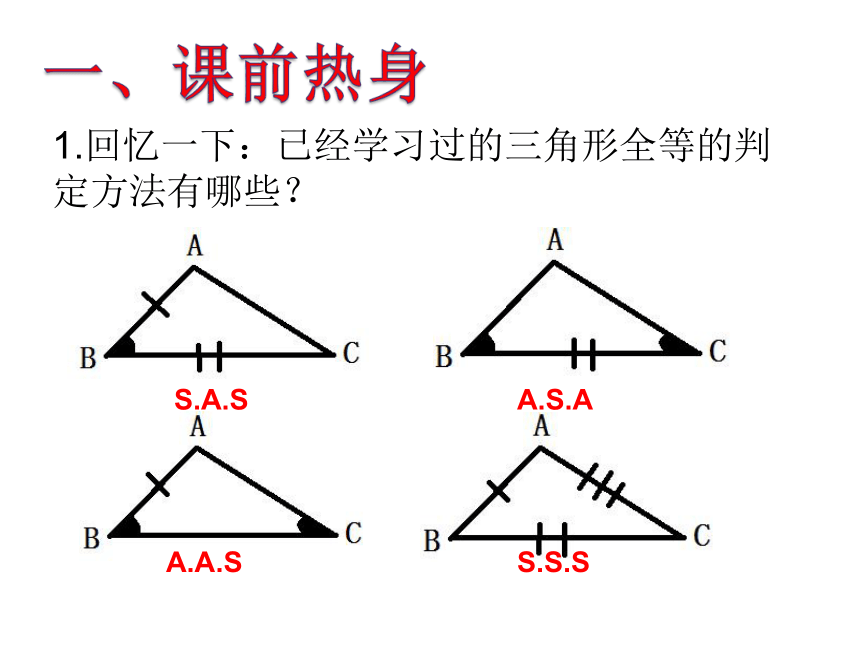
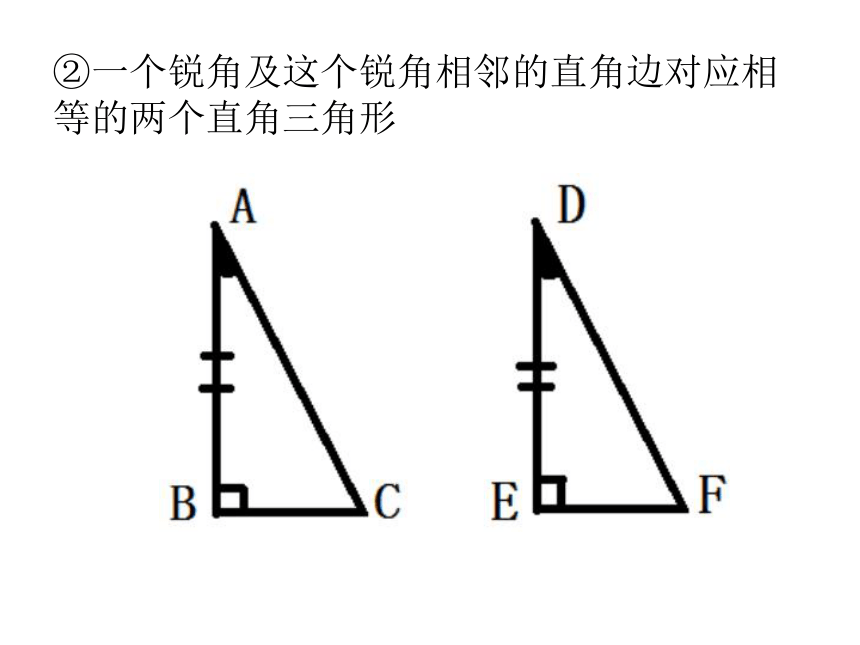
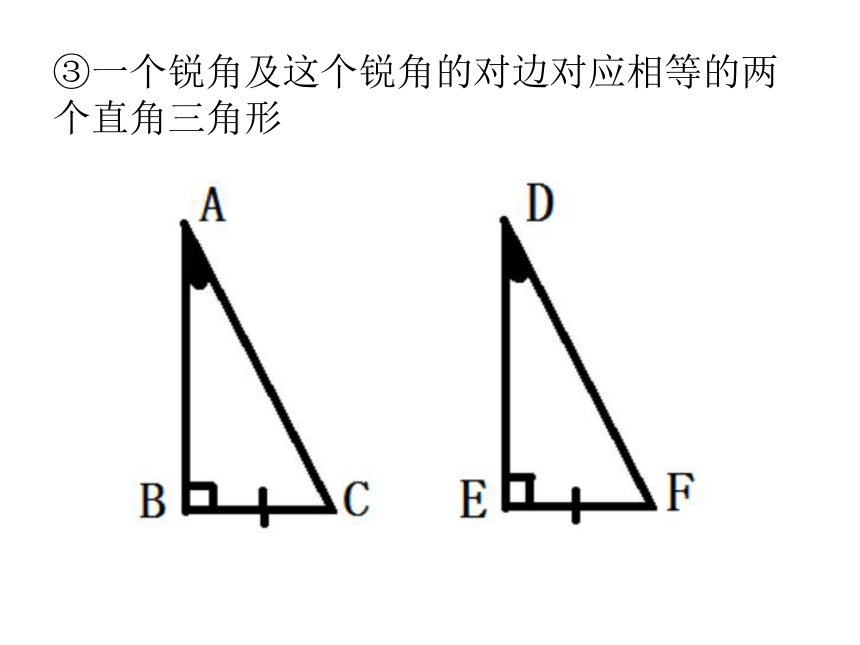
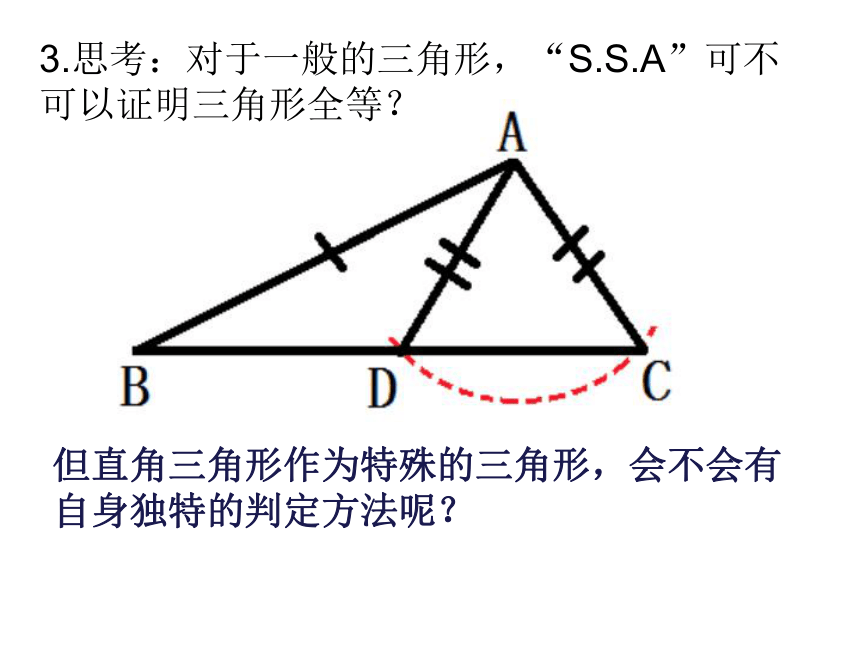
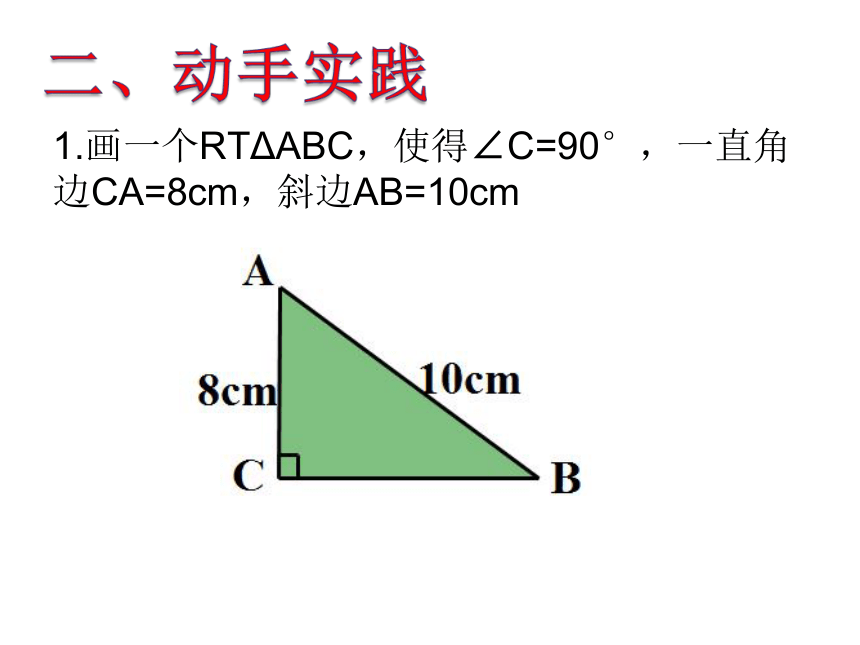
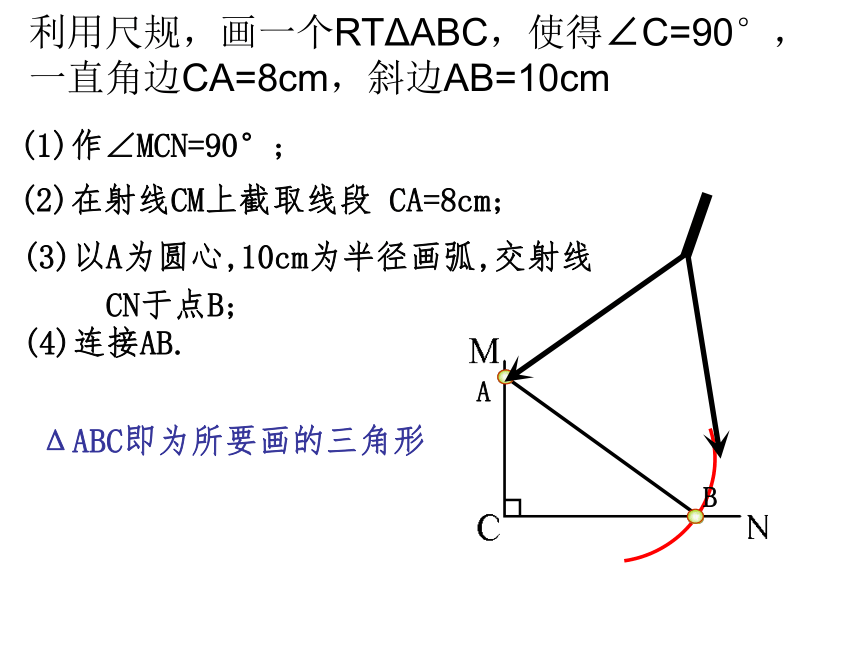
课件22张PPT。19.7直角三角形全等的判定1.回忆一下:已经学习过的三角形全等的判定方法有哪些?一、课前热身S.A.SA.S.AA.A.SS.S.S2.判断:满足下列条件的两个三角形是否全等?为什么?①两条直角边对应相等的两个直角三角形②一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形③一个锐角及这个锐角的对边对应相等的两个直角三角形④三边对应相等的直角三角形3.思考:对于一般的三角形,“S.S.A”可不可以证明三角形全等?但直角三角形作为特殊的三角形,会不会有自身独特的判定方法呢?1.画一个RTΔABC,使得∠C=90°,一直角边CA=8cm,斜边AB=10cm二、动手实践(1)作∠MCN=90°;(2)在射线CM上截取线段 CA=8cm;(3)以A为圆心,10cm为半径画弧,交射线
CN于点B; (4)连接AB.利用尺规,画一个RTΔABC,使得∠C=90°,一直角边CA=8cm,斜边AB=10cmΔABC即为所要画的三角形2.你发现了什么?如何证明?动手拼一拼两个三角形,你能拼出什么图形来帮助你的证明?动手拼一拼两个三角形,你能拼出什么图形来帮助你的证明?条件1,2用命题的方式来陈述我们刚刚证明的结论三、归纳新知如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等前提条件1条件1条件2直角三角形全等的判定定理:简写为“H.L”推理格式四、简单运用证:求证:在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.OABQDE五、角平分线性质定理逆定理的证明六、小结灵活运用各种方法证明直角三角形全等探究: 1:还需什么条件才能证明结论?探究:变式1:还需什么条件才能用H.L证明结论?探究:变式2:还需什么条件才能用H.L证明结论?还需什么条件才能证明结论?探究:变式3:1.图中有哪些全等三角形?
2.改变部分条件和结论是否仍然成立?3.在ΔACE向右平移的过程中,平分与全等的结论是否始终成立?进一步:谢谢!
CN于点B; (4)连接AB.利用尺规,画一个RTΔABC,使得∠C=90°,一直角边CA=8cm,斜边AB=10cmΔABC即为所要画的三角形2.你发现了什么?如何证明?动手拼一拼两个三角形,你能拼出什么图形来帮助你的证明?动手拼一拼两个三角形,你能拼出什么图形来帮助你的证明?条件1,2用命题的方式来陈述我们刚刚证明的结论三、归纳新知如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等前提条件1条件1条件2直角三角形全等的判定定理:简写为“H.L”推理格式四、简单运用证:求证:在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.OABQDE五、角平分线性质定理逆定理的证明六、小结灵活运用各种方法证明直角三角形全等探究: 1:还需什么条件才能证明结论?探究:变式1:还需什么条件才能用H.L证明结论?探究:变式2:还需什么条件才能用H.L证明结论?还需什么条件才能证明结论?探究:变式3:1.图中有哪些全等三角形?
2.改变部分条件和结论是否仍然成立?3.在ΔACE向右平移的过程中,平分与全等的结论是否始终成立?进一步:谢谢!
