沪教版八上:19.7 直角三角形全等的判定 课件(13张PPT)
文档属性
| 名称 | 沪教版八上:19.7 直角三角形全等的判定 课件(13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 477.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 14:56:52 | ||
图片预览




文档简介
课件13张PPT。19.7 直角三角形全等的判定(4)S.S.S:三条边对应相等的
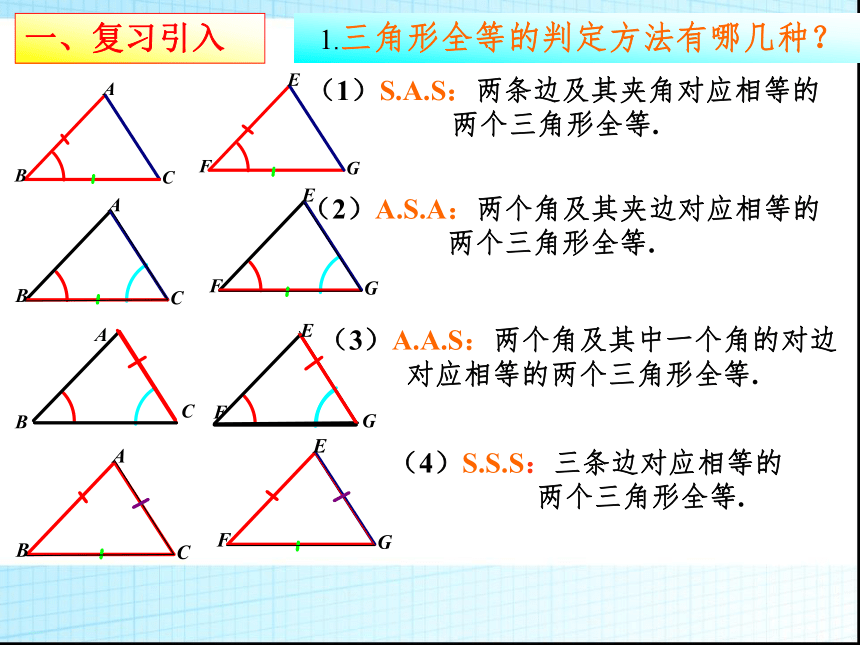
两个三角形全等. 1.三角形全等的判定方法有哪几种?一、复习引入(1)S.A.S:两条边及其夹角对应相等的
两个三角形全等.(2)A.S.A:两个角及其夹边对应相等的
两个三角形全等.(3)A.A.S:两个角及其中一个角的对边
对应相等的两个三角形全等.1.由题意作图形,标字母或符号;
2.三角形按角是怎样分类呢?三角形锐角三角形直角三角形钝角三角形问题 1:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。斜边和一条直角边对应相等的两个直角三角形是否全等?你能把这个问题用命题的形式来表述吗?问题2:证明一个命题是真命题,有哪几个步骤呢?2.由题设和结论,结合图形,写出“已知”和“求证”;3.先分析,写出证明过程。二、学习新知1、探究定理已知:如图,在△ABC与△A′B′C′中, 若AB=A′B′,AC=A′C′, ∠C=∠C′=90°.
求证:Rt△ABC≌Rt△A′B′C′.ABC分析:因为AC=A′C′,所以可通过图形的平移,使边AC与边A′C′重合,由于∠ACB=∠A′C′B′=90°,即∠BCB′=180°,因此点B、C、B′必在一条直线上,于是可以构造△ABB′是一个等腰三角形.证明:∵AB=A′B′∴∠B=∠B′(等边对等角).在△ABC与△A′B′C′中,
∠ACB=∠A′C′B′(已知),∠B=∠B′(已证),AB=A′B′(已知) ,∴Rt△ABC≌Rt△A′B′C′(A.A.S).(已知),把△ABC和△A′B′C′拼在一起,由于AC=A′C′,因此可使AC和A′C′重合;由于∠ACB=∠A′C′B′=90°,所以点B、C(C′)、B′三点必在一条直线上,于是得到△ABB′定理: 如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等(简记为H.L).ABCA′C′B′∟∟2、定理应用例题1 已知:如图,△ABC中,BD⊥AC,CE⊥AB,点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.证明:∵CE⊥AB,BD⊥AC(已知),∴△EBC和△DCB都是直角三角形.在Rt△EBC与Rt△DCB中,CE=BD (已知),BC=CB (公共边),∴Rt△EBC≌Rt△DCB(H.L).得∠EBC=∠DCB(全等三角形的对应角相等).∴AB=AC(等角对等边).即△ABC是等腰三角形.想一想还有其他的证明方法吗?F∟∟例题2 求证:在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.已知:如图,PC⊥OA,PD⊥OB,垂足分
别为点C、D,且PC=PD.
求证:点P在∠AOB的平分线上.证明:作射线OP.∵PC⊥OA,PD⊥OB(已知),∴∠PCO=∠PDO=90°(垂直的定义).在Rt△OPC与Rt△OPD中,PC=PDOP=(公共边),∴Rt△OPC≌Rt△OPD(H.L).得 ∠2=∠1(全等三角形的对应角相等),(已知),OP即OP是∠AOB的平分线(角平分线的定义).∴点P在∠AOB的平分线上.12分析:要证明点P在∠AOB的平分线上,那就要作出射线OP,只要证明∠POC=∠POD(即∠1=∠2).∟∟三、课堂反馈练习1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为点E、F.
求证:EB=FC.证明:∵AD是∠BAC的平分线, DE⊥AB, DF⊥AC (已知),∴DE=DF (在角的平分线上的点到这个角的两边的距离相等). △BDE和△CDF都是直角三角形.在Rt△BDE和Rt △CDF中,BD=CD(已知), DE=DF (已证),∴Rt△BDE≌Rt△CDF(H.L).∴EB=FC(全等三角形的对应边相等).ADFBE4、已知:如图,AD⊥CD,BC⊥CD,D、C分别为垂足,AB的垂直平分线EF交AB于点E,交CD于点F,BC=DF.
求证:AD=FC.C 四、课堂小结
通过本节课的学习你得到了哪些新知识,又有哪些收获?1.直角三角形全等的特殊的判定——“HL”定理.(注意:一般三角形全等的四种判定方法对直角三角形都适用)
2.运用“HL”定理时,前提条件必须是直角三角形,然后依据斜边和一条直角边对应相等,再证明两个直角三角形全等.五、作业布置
练习册 19.7
两个三角形全等. 1.三角形全等的判定方法有哪几种?一、复习引入(1)S.A.S:两条边及其夹角对应相等的
两个三角形全等.(2)A.S.A:两个角及其夹边对应相等的
两个三角形全等.(3)A.A.S:两个角及其中一个角的对边
对应相等的两个三角形全等.1.由题意作图形,标字母或符号;
2.三角形按角是怎样分类呢?三角形锐角三角形直角三角形钝角三角形问题 1:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。斜边和一条直角边对应相等的两个直角三角形是否全等?你能把这个问题用命题的形式来表述吗?问题2:证明一个命题是真命题,有哪几个步骤呢?2.由题设和结论,结合图形,写出“已知”和“求证”;3.先分析,写出证明过程。二、学习新知1、探究定理已知:如图,在△ABC与△A′B′C′中, 若AB=A′B′,AC=A′C′, ∠C=∠C′=90°.
求证:Rt△ABC≌Rt△A′B′C′.ABC分析:因为AC=A′C′,所以可通过图形的平移,使边AC与边A′C′重合,由于∠ACB=∠A′C′B′=90°,即∠BCB′=180°,因此点B、C、B′必在一条直线上,于是可以构造△ABB′是一个等腰三角形.证明:∵AB=A′B′∴∠B=∠B′(等边对等角).在△ABC与△A′B′C′中,
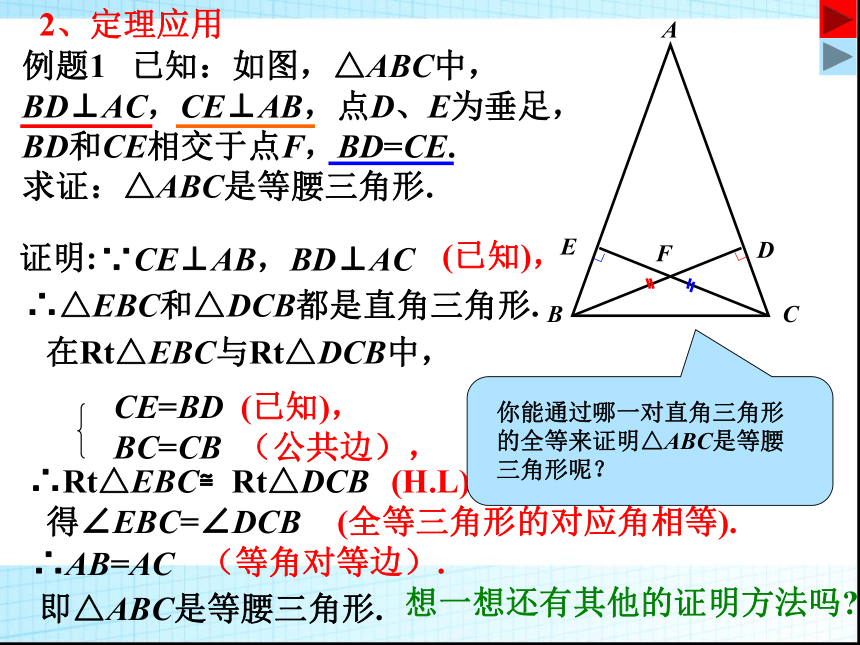
∠ACB=∠A′C′B′(已知),∠B=∠B′(已证),AB=A′B′(已知) ,∴Rt△ABC≌Rt△A′B′C′(A.A.S).(已知),把△ABC和△A′B′C′拼在一起,由于AC=A′C′,因此可使AC和A′C′重合;由于∠ACB=∠A′C′B′=90°,所以点B、C(C′)、B′三点必在一条直线上,于是得到△ABB′定理: 如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等(简记为H.L).ABCA′C′B′∟∟2、定理应用例题1 已知:如图,△ABC中,BD⊥AC,CE⊥AB,点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.证明:∵CE⊥AB,BD⊥AC(已知),∴△EBC和△DCB都是直角三角形.在Rt△EBC与Rt△DCB中,CE=BD (已知),BC=CB (公共边),∴Rt△EBC≌Rt△DCB(H.L).得∠EBC=∠DCB(全等三角形的对应角相等).∴AB=AC(等角对等边).即△ABC是等腰三角形.想一想还有其他的证明方法吗?F∟∟例题2 求证:在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.已知:如图,PC⊥OA,PD⊥OB,垂足分
别为点C、D,且PC=PD.
求证:点P在∠AOB的平分线上.证明:作射线OP.∵PC⊥OA,PD⊥OB(已知),∴∠PCO=∠PDO=90°(垂直的定义).在Rt△OPC与Rt△OPD中,PC=PDOP=(公共边),∴Rt△OPC≌Rt△OPD(H.L).得 ∠2=∠1(全等三角形的对应角相等),(已知),OP即OP是∠AOB的平分线(角平分线的定义).∴点P在∠AOB的平分线上.12分析:要证明点P在∠AOB的平分线上,那就要作出射线OP,只要证明∠POC=∠POD(即∠1=∠2).∟∟三、课堂反馈练习1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为点E、F.
求证:EB=FC.证明:∵AD是∠BAC的平分线, DE⊥AB, DF⊥AC (已知),∴DE=DF (在角的平分线上的点到这个角的两边的距离相等). △BDE和△CDF都是直角三角形.在Rt△BDE和Rt △CDF中,BD=CD(已知), DE=DF (已证),∴Rt△BDE≌Rt△CDF(H.L).∴EB=FC(全等三角形的对应边相等).ADFBE4、已知:如图,AD⊥CD,BC⊥CD,D、C分别为垂足,AB的垂直平分线EF交AB于点E,交CD于点F,BC=DF.
求证:AD=FC.C 四、课堂小结
通过本节课的学习你得到了哪些新知识,又有哪些收获?1.直角三角形全等的特殊的判定——“HL”定理.(注意:一般三角形全等的四种判定方法对直角三角形都适用)
2.运用“HL”定理时,前提条件必须是直角三角形,然后依据斜边和一条直角边对应相等,再证明两个直角三角形全等.五、作业布置
练习册 19.7
