沪教版(五四学制)八年级数学上册19.9 勾股定理 课件(21张PPT)
文档属性
| 名称 | 沪教版(五四学制)八年级数学上册19.9 勾股定理 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-15 19:54:53 | ||
图片预览







文档简介
课件21张PPT。九年制义务教育数学八年级(上册)(上教版)勾股定理学程学习检测学习目标导引学习流程设计学习效果检测知识拓展应用主要检测题型:口答;
笔答:A填空题,B判断题,C选择题,D计算题,E作图题,F证明题,G综合题 直角三角形两直角边的平方和等于斜边的平方。
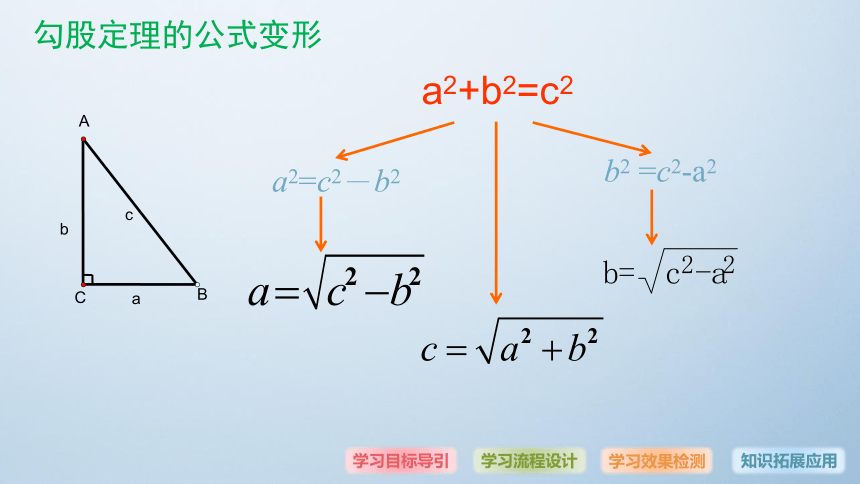
我们把这个定理叫勾股定理。一、复习旧知a2+b2=c2勾股定理的公式变形a2+b2=c2
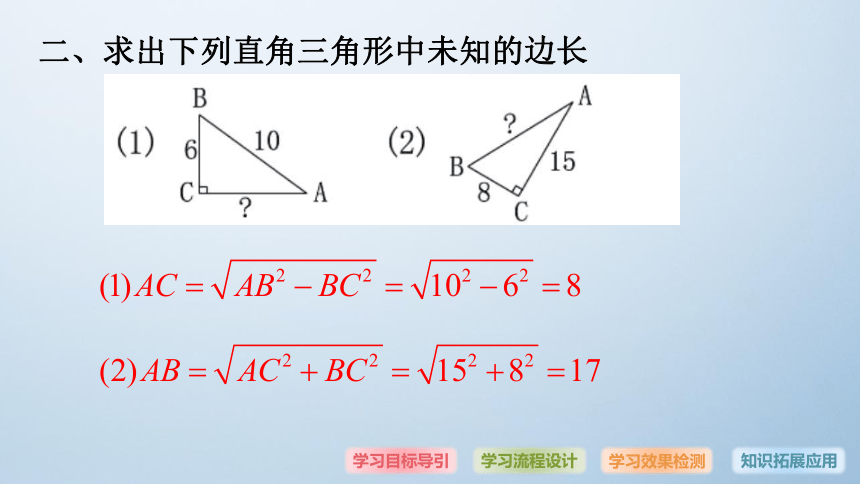
二、求出下列直角三角形中未知的边长三.运用勾股定理例题1一个门框的尺寸如图所示:
(1) 有一块长3米,宽0.8米的薄板能从门框内通过吗?
(2) 若薄木板长3米,宽1.5米呢?
(3) 若薄木板长3米,宽2.2米呢?
解:(1)能;0.8<1
(2)能;1.5<2
本题已将立体问题平面化,从而可以用平面几何方法解决问题。你知道能通过这个门框的最宽的木条吗?我国古代对勾股定理的应用就十分注重,在古代数学书籍中有不少相关记载.例如《九章算术》中的勾股问题,是具有历史地位的世界著名算题.例2:《九章算术》勾股章第6题“引葭赴岸”
“今有池方一丈,葭生其中央,出不一尺,引葭赴岸,适与岸齐.问水深,葭长各几何.”
分析:先把实际问题转化成数学问题。
解:BC=BD=(AB+1)
在Rt△ABC中:∠BAC= 90o
所以水深12尺,葭长13尺已知:AD = 1 尺, AC = 5尺,且∠CAB = 90o, BD =BC,求AB、BD的长.练习:一条小虫子从长方体三条边分别为3.4.5一个顶点A爬到另一个顶点C1,怎么爬最近?从表面上爬最短是多少?从表面上爬最短是如果这条虫子会钻洞是多少?四、利用勾股定理作长为无理数的线段探究:任何有理数都可以用数轴上的点把它表示出来.同样,任何无理数也都可以用数轴上的点把它表示出来.你能在数轴上画出表示 的点么?你能构造边长为 的线段吗? 可以看成以哪两个正整数为直角边的直角三角形的斜边?
在数轴上画出表示
步骤:1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
3、以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。
01A234BC-1C1、如图,在△ABC中,三边a,b,c的大小关系是( )
a8六、知识拓展应用2、一条小虫子从圆柱体表面的一个顶点A爬到另一个顶点B,怎么爬最近?如果这条小虫子会钻洞,所爬距离最近是多少?3、欣赏一颗下面美丽而神奇的勾股树。它是由古希腊数学家毕达哥拉斯根据勾股定理所画出来的勾股树也称为“毕达哥拉斯树”。它使我们大家深刻的感受到了几何之美。在欣赏之余思考最外围所有小正方形的面积之和与哪个正方形的面积相等?
希腊的著名数学家毕达哥拉斯发现了这个定理,因此世界上许多国家都称勾股定理为“毕达哥拉斯”定理。为了庆祝这一定理的发现,毕达哥拉斯学派杀了一百头牛酬谢供奉神灵,因此这个定理又有人叫做“百牛定理”. 我们可以先来看下列前三个图形中最外围所有小正方形的面积之和与哪个正方形的面积相等。
我们可以看到前三个图形的最外围所有小正方形的面积之和都与最大的那个正方形面积相等。
由此我们可以推理归纳得到“毕达哥拉斯树”的最外围所
有小正方形的面积之和也与那个最大的正方形面积相等。谢谢
笔答:A填空题,B判断题,C选择题,D计算题,E作图题,F证明题,G综合题 直角三角形两直角边的平方和等于斜边的平方。
我们把这个定理叫勾股定理。一、复习旧知a2+b2=c2勾股定理的公式变形a2+b2=c2
二、求出下列直角三角形中未知的边长三.运用勾股定理例题1一个门框的尺寸如图所示:
(1) 有一块长3米,宽0.8米的薄板能从门框内通过吗?
(2) 若薄木板长3米,宽1.5米呢?
(3) 若薄木板长3米,宽2.2米呢?
解:(1)能;0.8<1
(2)能;1.5<2
本题已将立体问题平面化,从而可以用平面几何方法解决问题。你知道能通过这个门框的最宽的木条吗?我国古代对勾股定理的应用就十分注重,在古代数学书籍中有不少相关记载.例如《九章算术》中的勾股问题,是具有历史地位的世界著名算题.例2:《九章算术》勾股章第6题“引葭赴岸”
“今有池方一丈,葭生其中央,出不一尺,引葭赴岸,适与岸齐.问水深,葭长各几何.”
分析:先把实际问题转化成数学问题。
解:BC=BD=(AB+1)
在Rt△ABC中:∠BAC= 90o
所以水深12尺,葭长13尺已知:AD = 1 尺, AC = 5尺,且∠CAB = 90o, BD =BC,求AB、BD的长.练习:一条小虫子从长方体三条边分别为3.4.5一个顶点A爬到另一个顶点C1,怎么爬最近?从表面上爬最短是多少?从表面上爬最短是如果这条虫子会钻洞是多少?四、利用勾股定理作长为无理数的线段探究:任何有理数都可以用数轴上的点把它表示出来.同样,任何无理数也都可以用数轴上的点把它表示出来.你能在数轴上画出表示 的点么?你能构造边长为 的线段吗? 可以看成以哪两个正整数为直角边的直角三角形的斜边?
在数轴上画出表示
步骤:1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
3、以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。
01A234BC-1C1、如图,在△ABC中,三边a,b,c的大小关系是( )
a
希腊的著名数学家毕达哥拉斯发现了这个定理,因此世界上许多国家都称勾股定理为“毕达哥拉斯”定理。为了庆祝这一定理的发现,毕达哥拉斯学派杀了一百头牛酬谢供奉神灵,因此这个定理又有人叫做“百牛定理”. 我们可以先来看下列前三个图形中最外围所有小正方形的面积之和与哪个正方形的面积相等。
我们可以看到前三个图形的最外围所有小正方形的面积之和都与最大的那个正方形面积相等。
由此我们可以推理归纳得到“毕达哥拉斯树”的最外围所
有小正方形的面积之和也与那个最大的正方形面积相等。谢谢
