沪教版(五四学制)八年级数学上册19.10 两点的距离公式 课件(19张PPT)
文档属性
| 名称 | 沪教版(五四学制)八年级数学上册19.10 两点的距离公式 课件(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 515.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-15 20:03:34 | ||
图片预览






文档简介
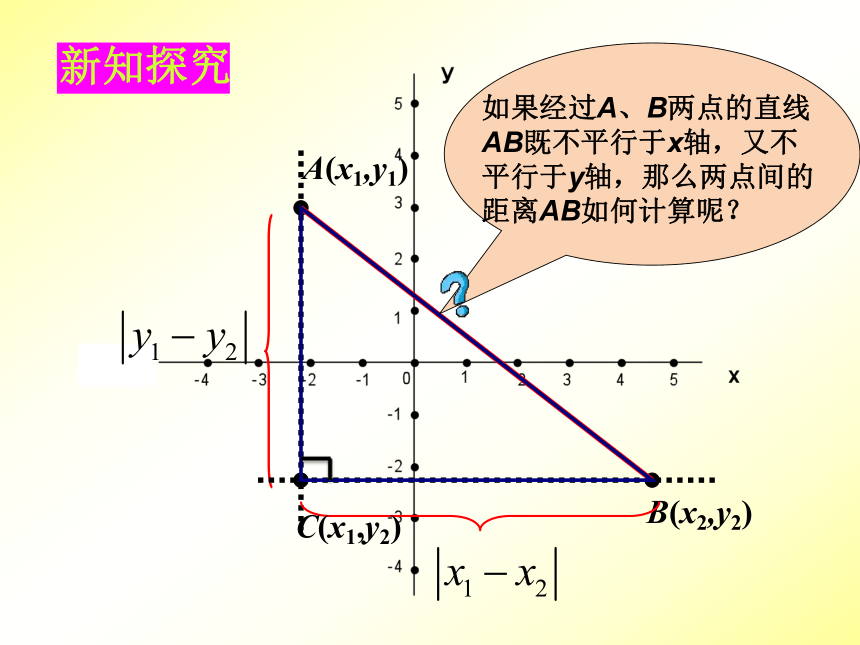
课件19张PPT。19.10 两点的距离公式 复习引入 在直角坐标平面内, A(x , y1) 、B(x ,y2),那么A、B两点间的距离公式是什么?AB= (1) y轴或平行于y轴的直线上的点的坐标有什么特征? 点的横坐标相同复习引入 在直角坐标平面内, A(x , y1) 、B(x ,y2),那么A、B两点间的距离公式是什么?AB= (1) y轴或平行于y轴的直线上的点的坐标有什么特征? (2) x轴或平行于x轴的直线上的点的坐标有什么特征? C(x1,y) 、D(x2,y),那么C、D两点间的距离公式是什么?CD=点的纵坐标相同B(x2,y2)如果经过A、B两点的直线AB既不平行于x轴,又不平行于y轴,那么两点间的距离AB如何计算呢?A(x1,y1)C(x1,y2)新知探究新课:在直角坐标平面内, AB两点间距离公式:若有两点同在x轴或y轴上,或者所在的直线平行于坐标轴时,这个公式适用吗?当两点同在x轴或平行于x轴的直线上时公式照样适用y1=y2当两点同在y轴或平行于y轴的直线上时x1=x2,AB= AB=
已知直角坐标平面内的两点分别为A(-3,2),B(1,-1),
求A、B两点的距离.例题1解:∵ ∴ (两点距离公式)试一试:1. 求下列两点的距离: 2) C (-3,5) D (7,-2)1) A(1,2) B(4,6)3) E(-4,3) F(1,3)4) G(-5,6) H(-3,-4)已知直角坐标平面内的△ABC三个顶点A、B、C的坐标分别为(-1,4)、(-4,-2)、(2,-5),试判断△ABC的形状. 分析:要判断△ABC的形状需先求出什么?如何判断? 解:∵ (两点距离公式) ∴AB=BC (等量代换) ∴(等量代换) ∴∠B=90°(勾股定理的逆定理).
∴△ABC是等腰直角三角形(等腰直角三角形定义)例题2试一试:已知三角形三个顶点的坐标,判断的三角形的形状1)解:(两点的距离公式)所以, △ABC 既不是等腰三角形也不是直角三角形.(1)A(-3,1)、B(1,4)、C(-6,-4);(2)E(4,3)、F(1,2)、G(3,-4);2)解:(两点的距离公式)所以 所以, △ABC是直角三角形。(勾股定理逆定理)(2)E(4,3)、F(1,2)、G(3,-4);试一试:已知直角坐标平面内y轴上有一点A到点B(4,1) 的距离为5,求点A坐标。思考题1: 解:设点A(0,y).
∵ (两点距离公式),
∵ B(4,1),AB=5.
∴ y=4或y=-2
∴ A(0,4)或A(0,-2)解:点P在x轴上,可设点P的坐标为(m,0).得(两点距离公式).
∵PA=PB(已知),
∴即=解得
已知直角坐标平面内的两点分别为A(3,3),
B(6,1),点P在x轴上,且PA=PB,求点P的坐标. ∴点P的坐标是 例题分析例题3思考题:
已知直角坐标平面内的两点分别为A(3,3),
B(6,1),点P在x轴上,
点P有几个?如何求出点P的坐标? △PAB是等腰三角形 分析:此时△PAB中并未指明那两条边相等,因而需要分类讨论,按照“PA=PB”、“ PA=AB”、“ PB=AB”三种情况讨论 小组讨论 思考题:
已知直角坐标平面内的两点分别为A(3,3),B(6,1),点P在x轴上,且△PAB是等腰三角形,你如何求出点P的坐标? 小组讨论得=13解得此时点P的坐标是...得=13解得此时点P的坐是 .
∴点P的坐标是 ,
.
已知直角坐标平面内的两点分别为A(3,3),B(6,1),点P在y轴上,且△PAB是等腰三角形,你如何求出点P的坐标? 试一试:试一试:已知等边三角形ABC的顶点B、C的坐标分别为
(0,0)和(4,0),求顶点A的坐标.如果直角坐标平面内有两点,那么 、
两点的距离.自主小结 2.本节课中所涉及到的数学思想? 数形结合、分类讨论、方程思想回家作业1、思考题、试一试
2、练习册 习题19.10 今天的课就上到这里
已知直角坐标平面内的两点分别为A(-3,2),B(1,-1),
求A、B两点的距离.例题1解:∵ ∴ (两点距离公式)试一试:1. 求下列两点的距离: 2) C (-3,5) D (7,-2)1) A(1,2) B(4,6)3) E(-4,3) F(1,3)4) G(-5,6) H(-3,-4)已知直角坐标平面内的△ABC三个顶点A、B、C的坐标分别为(-1,4)、(-4,-2)、(2,-5),试判断△ABC的形状. 分析:要判断△ABC的形状需先求出什么?如何判断? 解:∵ (两点距离公式) ∴AB=BC (等量代换) ∴(等量代换) ∴∠B=90°(勾股定理的逆定理).
∴△ABC是等腰直角三角形(等腰直角三角形定义)例题2试一试:已知三角形三个顶点的坐标,判断的三角形的形状1)解:(两点的距离公式)所以, △ABC 既不是等腰三角形也不是直角三角形.(1)A(-3,1)、B(1,4)、C(-6,-4);(2)E(4,3)、F(1,2)、G(3,-4);2)解:(两点的距离公式)所以 所以, △ABC是直角三角形。(勾股定理逆定理)(2)E(4,3)、F(1,2)、G(3,-4);试一试:已知直角坐标平面内y轴上有一点A到点B(4,1) 的距离为5,求点A坐标。思考题1: 解:设点A(0,y).
∵ (两点距离公式),
∵ B(4,1),AB=5.
∴ y=4或y=-2
∴ A(0,4)或A(0,-2)解:点P在x轴上,可设点P的坐标为(m,0).得(两点距离公式).
∵PA=PB(已知),
∴即=解得
已知直角坐标平面内的两点分别为A(3,3),
B(6,1),点P在x轴上,且PA=PB,求点P的坐标. ∴点P的坐标是 例题分析例题3思考题:
已知直角坐标平面内的两点分别为A(3,3),
B(6,1),点P在x轴上,
点P有几个?如何求出点P的坐标? △PAB是等腰三角形 分析:此时△PAB中并未指明那两条边相等,因而需要分类讨论,按照“PA=PB”、“ PA=AB”、“ PB=AB”三种情况讨论 小组讨论 思考题:
已知直角坐标平面内的两点分别为A(3,3),B(6,1),点P在x轴上,且△PAB是等腰三角形,你如何求出点P的坐标? 小组讨论得=13解得此时点P的坐标是...得=13解得此时点P的坐是 .
∴点P的坐标是 ,
.
已知直角坐标平面内的两点分别为A(3,3),B(6,1),点P在y轴上,且△PAB是等腰三角形,你如何求出点P的坐标? 试一试:试一试:已知等边三角形ABC的顶点B、C的坐标分别为
(0,0)和(4,0),求顶点A的坐标.如果直角坐标平面内有两点,那么 、
两点的距离.自主小结 2.本节课中所涉及到的数学思想? 数形结合、分类讨论、方程思想回家作业1、思考题、试一试
2、练习册 习题19.10 今天的课就上到这里
