人教版小学六年级数学上册 第8章 数学广角-数与形 单元测试题(有答案)
文档属性
| 名称 | 人教版小学六年级数学上册 第8章 数学广角-数与形 单元测试题(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 166.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-12 15:30:42 | ||
图片预览



文档简介
人教版小学六年级数学上册 第8章 数学广角-数与形 单元测试题
一.选择题(共8小题)
1.巍巍宝塔共七层,红光点点倍加增.塔尖若有n盏灯,七层共需灯几盏?这首古诗的意思是:一座七层的宝塔,从上到下每层灯的数量都是上面一层的2倍.如果最上面塔尖这一层有n盏灯,那么这座宝塔一共有( )盏灯.
A.2n B.7n C.49n D.127n
2.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆…依此规律,第10个图形中小圆的个数为( )
A.136 B.114 C.112 D.106
3.仔细观察37×3=111;37×6=222;37×9=333;请你推算出37×21的得数是( )
A.444 B.555 C.777
4.根据你发现的规律,算式1234567×8+7的得数是( )
A.9876 B.98765 C.987654 D.9876543
5.在100、95、90、……、15、10、5这列数中,第11个数是( )
A.55 B.50 C.45 D.60
6.1、2、3、2、3、4、3、4、5、4、5、6…,照这样从左数第50个数是( )
A.50 B.17 C.18 D.19
7.0.123412341234…,小数点后第100个数字是( )
A.1 B.2 C.3 D.4
8.2. 0小数部分的第100位数字是( )
A.5 B.0 C.4
二.填空题(共9小题)
9.阴影部分表示38,如图所示的长方形表示 .
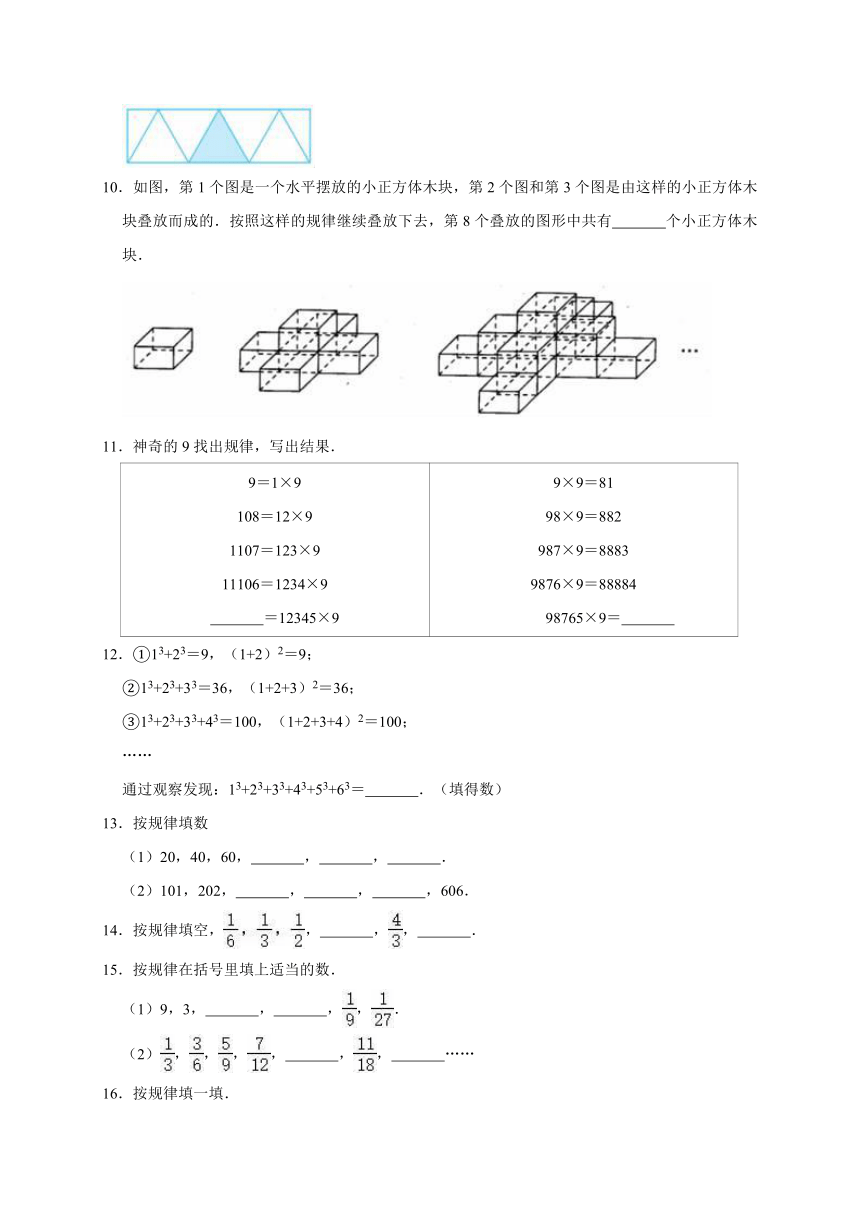
10.如图,第1个图是一个水平摆放的小正方体木块,第2个图和第3个图是由这样的小正方体木块叠放而成的.按照这样的规律继续叠放下去,第8个叠放的图形中共有 个小正方体木块.
11.神奇的9找出规律,写出结果.
9=1×9108=12×91107=123×911106=1234×9 =12345×9 9×9=8198×9=882987×9=88839876×9=8888498765×9=
12.①13+23=9,(1+2)2=9;
②13+23+33=36,(1+2+3)2=36;
③13+23+33+43=100,(1+2+3+4)2=100;
……
通过观察发现:13+23+33+43+53+63= .(填得数)
13.按规律填数
(1)20,40,60, , , .
(2)101,202, , , ,606.
14.按规律填空,, ,, .
15.按规律在括号里填上适当的数.
(1)9,3, , ,,.
(2),,,, ,, ……
16.按规律填一填.
(1)4001,5002,6003, ,8005.
(2)8600,8400,8200,8000, .
17.如图所示的运算程序中,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2014次输出的结果为 .
三.判断题(共5小题)
18.1除以111的商的小数部分第15位数字是0 .(判断对错)
19.按1、8、27、 、125、216的规律排,横线中的数应为64. .(判断对错)
20.44×9=396,444×9=3996,由此可得44444×9=399996. (判断对错)
21.如图,如果一个小三角形的边长为1cm,第五个图形的周长是15cm. .(判断对错)
22.如图:
那么第7个点阵有45个点. .(判断对错)
四.计算题(共1小题)
23.看算式,找规律,填答案.
①88.2÷9=9.8 ②88.83÷9=9.87 ③88.884÷9=9.876
④88.8885÷9= ⑤88.88886÷9= ⑥88.888887÷9=
五.应用题(共2小题)
24.在六一联欢晚会上,有一个“亲子互动”节目,用火柴棒摆“金鱼”比赛.如图所示,按照下面的规律摆下去.
(1)摆4条“金鱼”需要多少根火柴棒?
(2)用122根火柴棒可以摆多少条“金鱼”?
25.如图,一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人……照这样,10张桌子并成一排可以坐多少人?如果一共要坐62人,需要并多少张桌子才能坐下?
参考答案与试题解析
一.选择题(共8小题)
1.解:假设最上边的一层是n盏灯,
则:n+2n+4n+8n+16n+32n+64n=127n(盏)
答:这座宝塔一共有127n盏灯.
故选:D.
2.解:10×11+4
=110+4
=114(个)
答:第10个图形中小圆的个数为114个.
故选:B.
3.解:37×21=37×3×7=111×7=777
故选:C.
4.解:1+9=2+8=3+7=4+6=5+5=6+4=7+3,
算式1234567×8+7=9876543.
故选:D.
5.解:在100、95、90、……、15、10、5这列数中,第11个数是50.
故选:B.
6.解:这个数列每三个数看成一组,那么:
50÷3=16…2;
50就是第17组数中的第二个;
它是:17+1=18;
故选:C.
7.解:小数0.123412341234…循环节为1234,共4位数.
100÷4=25,
小数点后第100个数字是4.
故选:D.
8.解:因为2. 0的循环节是504,100÷3=33…1,
所以第100个数字是5.
故选:A.
二.填空题(共9小题)
9.解:38
=38×
=456
答:长方形表示 456.
10.解:根据题干分析可得:前几个图形依次增加的小正方体方块的个数分别是12+4、32+4、52+4、72+4,…,
所以第8个叠放的图形中共有1+12+4+32+4+52+4+72+4+92+4+112+4+132+4
=1+1+4+9+4+25+4+49+4+81+4+121+4+169+4
=484(个)
答:第8个叠放的图形中共有 484个小正方体木块.
故答案为:484.
11.解:
9=1×9108=12×91107=123×911106=1234×9111105=12345×9 9×9=8198×9=882987×9=88839876×9=8888498765×9=888885
故答案为:111105,888885.
12.解:13+23+33+43+53+63
=(1+2+3+4+5+6)2
=212
=441
即通过观察发现:13+23+33+43+53+63=441.
故答案为:441.
13.解:(1)60+20=80
80+20=100
100+20=120
即20,40,60,80,100,120.
(2)202+101=303
303+101=404
404+101=505
即101,202,303,404,505,606.
故答案为:80,100,120;303,404,505.
14.解:=,=,=,
=
=
故答案为:;.
15.解:根据分析可得,
(1)3÷3=1
1÷3=
(2)=
=
故答案为:1,;,.
16.解:根据分析可得,
(1)6003+1001=7004
(2)8000﹣200=7800
故答案为:7004,7800.
17.解:当输入x=48时,第一次输出48×=24;当输入x=24时,第二次输出24×=12;
当输入x=12时,第三次输出12×=6;
当输入x=6时,第四次输出6×=3;
当输入x=3时,第五次输出3+3=6;
当输入x=6时,第六次输出6×=3;
…
故第2014次输出的结果为3,
故答案为:3
三.判断题(共5小题)
18.解:1÷111=0.009009…,循环节是009,三位,15÷3=5,所以商的小数部分第15位数字是9.
故答案为:×.
19.解:13=1;23=8;3 3=27;43=64;5 3=125; 63=216.
由此发现规律:以上数列是按1、2、3、4、5、6的立方顺序排列的,43=64.
故答案为:正确.
20.解:因为44×9=396
444×9=3996
所以44444×9=399996.
故答案为:√.
21.解:根据题干分析可得:当有n个三角形时,图形周长=边长×(n+2),
当n=5时,图形周长是:1×(5+2)=7(cm),
答:第五个图形的周长是7cm.
故答案为:×.
22.解:1+4+6+8+10+12+14=55
55>45
所以第7个点阵有45个点的说法是错误的;
故答案为:×.
四.计算题(共1小题)
23.解:看算式,找规律,填答案.
①88.2÷9=9.8
②88.83÷9=9.87
③88.884÷9=9.876
④88.8885÷9=9.8765
⑤88.88886÷9=9.87654
⑥88.888887÷9=9.876543.
故答案为:9.8765,9.87654,9.876543.
五.应用题(共2小题)
24.解:摆1条“金鱼”需要火柴棒:8根;
摆2条“金鱼”需要火柴棒:8+6=14(根);
摆3条“金鱼”需要火柴棒:8+6+6=20(根);
……
摆n条“金鱼”需要火柴棒:8+6(n﹣1)=(6n+2)根.
(1)摆4条“金鱼”需要火柴棒:
4×6+2
=24+2
=26(根)
答:摆4条“金鱼”需要26根火柴棒.
(2)6n+2=122
6n=120
n=20
答:用122根火柴棒可以摆2条“金鱼”.
25.解:根据题意得:n张桌子并起来坐(2+4n)人;
10张桌子并成一排可以坐的人数:
2+4×10
=2+40
=42(人)
要坐62人,要求需要并多少张桌子,运用关系式:2+4n=62,
可得桌子数:
(62﹣2)÷4
=60÷4
=15(张)
答:10张桌子并成一排可以坐42人,如果一共要坐62人,需要并15张桌子才能坐下.
一.选择题(共8小题)
1.巍巍宝塔共七层,红光点点倍加增.塔尖若有n盏灯,七层共需灯几盏?这首古诗的意思是:一座七层的宝塔,从上到下每层灯的数量都是上面一层的2倍.如果最上面塔尖这一层有n盏灯,那么这座宝塔一共有( )盏灯.
A.2n B.7n C.49n D.127n
2.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆…依此规律,第10个图形中小圆的个数为( )
A.136 B.114 C.112 D.106
3.仔细观察37×3=111;37×6=222;37×9=333;请你推算出37×21的得数是( )
A.444 B.555 C.777
4.根据你发现的规律,算式1234567×8+7的得数是( )
A.9876 B.98765 C.987654 D.9876543
5.在100、95、90、……、15、10、5这列数中,第11个数是( )
A.55 B.50 C.45 D.60
6.1、2、3、2、3、4、3、4、5、4、5、6…,照这样从左数第50个数是( )
A.50 B.17 C.18 D.19
7.0.123412341234…,小数点后第100个数字是( )
A.1 B.2 C.3 D.4
8.2. 0小数部分的第100位数字是( )
A.5 B.0 C.4
二.填空题(共9小题)
9.阴影部分表示38,如图所示的长方形表示 .
10.如图,第1个图是一个水平摆放的小正方体木块,第2个图和第3个图是由这样的小正方体木块叠放而成的.按照这样的规律继续叠放下去,第8个叠放的图形中共有 个小正方体木块.
11.神奇的9找出规律,写出结果.
9=1×9108=12×91107=123×911106=1234×9 =12345×9 9×9=8198×9=882987×9=88839876×9=8888498765×9=
12.①13+23=9,(1+2)2=9;
②13+23+33=36,(1+2+3)2=36;
③13+23+33+43=100,(1+2+3+4)2=100;
……
通过观察发现:13+23+33+43+53+63= .(填得数)
13.按规律填数
(1)20,40,60, , , .
(2)101,202, , , ,606.
14.按规律填空,, ,, .
15.按规律在括号里填上适当的数.
(1)9,3, , ,,.
(2),,,, ,, ……
16.按规律填一填.
(1)4001,5002,6003, ,8005.
(2)8600,8400,8200,8000, .
17.如图所示的运算程序中,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2014次输出的结果为 .
三.判断题(共5小题)
18.1除以111的商的小数部分第15位数字是0 .(判断对错)
19.按1、8、27、 、125、216的规律排,横线中的数应为64. .(判断对错)
20.44×9=396,444×9=3996,由此可得44444×9=399996. (判断对错)
21.如图,如果一个小三角形的边长为1cm,第五个图形的周长是15cm. .(判断对错)
22.如图:
那么第7个点阵有45个点. .(判断对错)
四.计算题(共1小题)
23.看算式,找规律,填答案.
①88.2÷9=9.8 ②88.83÷9=9.87 ③88.884÷9=9.876
④88.8885÷9= ⑤88.88886÷9= ⑥88.888887÷9=
五.应用题(共2小题)
24.在六一联欢晚会上,有一个“亲子互动”节目,用火柴棒摆“金鱼”比赛.如图所示,按照下面的规律摆下去.
(1)摆4条“金鱼”需要多少根火柴棒?
(2)用122根火柴棒可以摆多少条“金鱼”?
25.如图,一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人……照这样,10张桌子并成一排可以坐多少人?如果一共要坐62人,需要并多少张桌子才能坐下?
参考答案与试题解析
一.选择题(共8小题)
1.解:假设最上边的一层是n盏灯,
则:n+2n+4n+8n+16n+32n+64n=127n(盏)
答:这座宝塔一共有127n盏灯.
故选:D.
2.解:10×11+4
=110+4
=114(个)
答:第10个图形中小圆的个数为114个.
故选:B.
3.解:37×21=37×3×7=111×7=777
故选:C.
4.解:1+9=2+8=3+7=4+6=5+5=6+4=7+3,
算式1234567×8+7=9876543.
故选:D.
5.解:在100、95、90、……、15、10、5这列数中,第11个数是50.
故选:B.
6.解:这个数列每三个数看成一组,那么:
50÷3=16…2;
50就是第17组数中的第二个;
它是:17+1=18;
故选:C.
7.解:小数0.123412341234…循环节为1234,共4位数.
100÷4=25,
小数点后第100个数字是4.
故选:D.
8.解:因为2. 0的循环节是504,100÷3=33…1,
所以第100个数字是5.
故选:A.
二.填空题(共9小题)
9.解:38
=38×
=456
答:长方形表示 456.
10.解:根据题干分析可得:前几个图形依次增加的小正方体方块的个数分别是12+4、32+4、52+4、72+4,…,
所以第8个叠放的图形中共有1+12+4+32+4+52+4+72+4+92+4+112+4+132+4
=1+1+4+9+4+25+4+49+4+81+4+121+4+169+4
=484(个)
答:第8个叠放的图形中共有 484个小正方体木块.
故答案为:484.
11.解:
9=1×9108=12×91107=123×911106=1234×9111105=12345×9 9×9=8198×9=882987×9=88839876×9=8888498765×9=888885
故答案为:111105,888885.
12.解:13+23+33+43+53+63
=(1+2+3+4+5+6)2
=212
=441
即通过观察发现:13+23+33+43+53+63=441.
故答案为:441.
13.解:(1)60+20=80
80+20=100
100+20=120
即20,40,60,80,100,120.
(2)202+101=303
303+101=404
404+101=505
即101,202,303,404,505,606.
故答案为:80,100,120;303,404,505.
14.解:=,=,=,
=
=
故答案为:;.
15.解:根据分析可得,
(1)3÷3=1
1÷3=
(2)=
=
故答案为:1,;,.
16.解:根据分析可得,
(1)6003+1001=7004
(2)8000﹣200=7800
故答案为:7004,7800.
17.解:当输入x=48时,第一次输出48×=24;当输入x=24时,第二次输出24×=12;
当输入x=12时,第三次输出12×=6;
当输入x=6时,第四次输出6×=3;
当输入x=3时,第五次输出3+3=6;
当输入x=6时,第六次输出6×=3;
…
故第2014次输出的结果为3,
故答案为:3
三.判断题(共5小题)
18.解:1÷111=0.009009…,循环节是009,三位,15÷3=5,所以商的小数部分第15位数字是9.
故答案为:×.
19.解:13=1;23=8;3 3=27;43=64;5 3=125; 63=216.
由此发现规律:以上数列是按1、2、3、4、5、6的立方顺序排列的,43=64.
故答案为:正确.
20.解:因为44×9=396
444×9=3996
所以44444×9=399996.
故答案为:√.
21.解:根据题干分析可得:当有n个三角形时,图形周长=边长×(n+2),
当n=5时,图形周长是:1×(5+2)=7(cm),
答:第五个图形的周长是7cm.
故答案为:×.
22.解:1+4+6+8+10+12+14=55
55>45
所以第7个点阵有45个点的说法是错误的;
故答案为:×.
四.计算题(共1小题)
23.解:看算式,找规律,填答案.
①88.2÷9=9.8
②88.83÷9=9.87
③88.884÷9=9.876
④88.8885÷9=9.8765
⑤88.88886÷9=9.87654
⑥88.888887÷9=9.876543.
故答案为:9.8765,9.87654,9.876543.
五.应用题(共2小题)
24.解:摆1条“金鱼”需要火柴棒:8根;
摆2条“金鱼”需要火柴棒:8+6=14(根);
摆3条“金鱼”需要火柴棒:8+6+6=20(根);
……
摆n条“金鱼”需要火柴棒:8+6(n﹣1)=(6n+2)根.
(1)摆4条“金鱼”需要火柴棒:
4×6+2
=24+2
=26(根)
答:摆4条“金鱼”需要26根火柴棒.
(2)6n+2=122
6n=120
n=20
答:用122根火柴棒可以摆2条“金鱼”.
25.解:根据题意得:n张桌子并起来坐(2+4n)人;
10张桌子并成一排可以坐的人数:
2+4×10
=2+40
=42(人)
要坐62人,要求需要并多少张桌子,运用关系式:2+4n=62,
可得桌子数:
(62﹣2)÷4
=60÷4
=15(张)
答:10张桌子并成一排可以坐42人,如果一共要坐62人,需要并15张桌子才能坐下.
