人教版小学六年级数学上册 第8章 数学广角-数与形 单元测试题1(有答案)
文档属性
| 名称 | 人教版小学六年级数学上册 第8章 数学广角-数与形 单元测试题1(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 122.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-12 15:37:11 | ||
图片预览



文档简介
人教版小学六年级数学上册 第8章 数学广角-数与形 单元测试题
一.选择题(共8小题)
1.观察下面的点阵图形,根据圆点的变化,探究其规律,则第8个图形中圆点的个数为( )
A.25 B.26 C.27 D.29
2.如表,照这样的规律摆下去,当图形中有17个圆时,正方形有( )个.
A.8 B.9 C.18 D.35
3.下面算式中,与1+3+5+7+9+7+5+3+1的得数相等的是( )
A.52+32 B.42+52 C.52﹣32
4.已知99×99=9801,999×999=9980019999×9999=99980001,下一个式子是( )
A.99999×99999=999800001
B.99999×99999=9999800001
C.99999×99999=9999980001
D.99999×99999=99999980001
5.找规律1,2,4,7,11,__,___,29.横线上应填( )
A.15,19 B.16,22 C.16,21
6.按数的顺序填空:41、40、( )、38.
A.39 B.42 C.37 D.40
7.根据3×4=12、33×34=1122、333×334=111222,推测3333×3334=( )
A.11111222 B.11122222 C.11112222 D.11111112
8.循环小数的小数部分的第50位上的数字是( )
A.5 B.6 C.7
二.填空题(共9小题)
9.小明在社会大课堂的研学活动中,发现中式建筑中的窗格
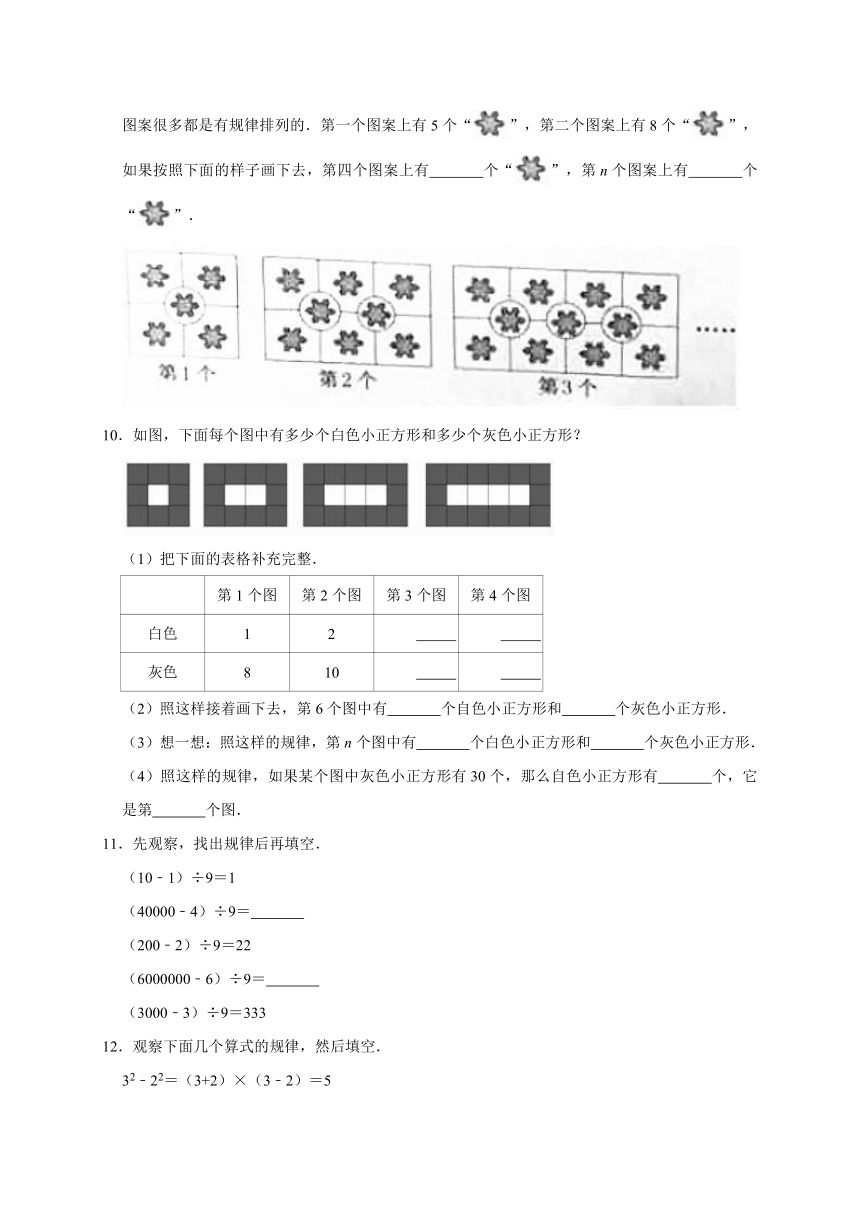
图案很多都是有规律排列的.第一个图案上有5个“”,第二个图案上有8个“”,如果按照下面的样子画下去,第四个图案上有 个“”,第n个图案上有 个“”.
10.如图,下面每个图中有多少个白色小正方形和多少个灰色小正方形?
(1)把下面的表格补充完整.
第1个图 第2个图 第3个图 第4个图
白色 1 2
灰色 8 10
(2)照这样接着画下去,第6个图中有 个自色小正方形和 个灰色小正方形.
(3)想一想:照这样的规律,第n个图中有 个白色小正方形和 个灰色小正方形.
(4)照这样的规律,如果某个图中灰色小正方形有30个,那么自色小正方形有 个,它是第 个图.
11.先观察,找出规律后再填空.
(10﹣1)÷9=1
(40000﹣4)÷9=
(200﹣2)÷9=22
(6000000﹣6)÷9=
(3000﹣3)÷9=333
12.观察下面几个算式的规律,然后填空.
32﹣22=(3+2)×(3﹣2)=5
42﹣32=(4+3)×(4﹣3)=7
52﹣42=(5+4)×(5﹣4)=9
62﹣52=(6+5)×(6﹣5)=11
……
20182﹣20172= = .
13.找规律填数:100,50,25, , .
14.图中各数之间存在一定的规律,根据规律可以知道a= .
15.按规律继续填数:
10、13、16、19、 、 、 .
18、27、36、45、 、 、 .
16.按规律填数
(1)1、2、5、 、17、26、37、50.
(2)1、1、2、3、5、8、 、21、34.
17.通过计算发现规律.
6543﹣2345=
9876﹣5678=
7654﹣3456=
按找到的规律,再写两个算式.
三.判断题(共5小题)
18.19.小数点后第80位上的数字是2. .(判断对错)
19.一个数列为:1,2,3,1,2,3,…按这样的顺序排下去,第20个数是3. (判断对错)
20.根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果. .(判断对错)
21.用小棒照图搭正方形,搭一个正方形用4根,搭两个正方形用7根,搭a个正方形有4a根. .(判断对错)
22.摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要31根小棒. .(判断对错)
四.计算题(共1小题)
23.先用计算器计算出横线里是几,再根据规律直接写出后两道题的结果.
1×9=9
2×99= 9
3×999= 99
4×9999= 999
5×99999=
6×999999=
五.应用题(共2小题)
24.小明用小棒搭房子.搭2间用9根,搭3间用13根.照这样计算,如果搭10间房子,需要用多少根小棒?
25.小明用面积为1cm2的正方形卡纸拼摆图形.
(1)像这样拼下去,第(5)个图形要用多少张小正方形卡纸?
(2)如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要多少厘米铁丝?
参考答案与试题解析
一.选择题(共8小题)
1.解:由分析可图可知,第n个图的点数是(4n﹣3)个
第8个图形中圆点的个数为:
4×8﹣3
=32﹣3
=29
答:第8个图形中圆点的个数为29.
故选:D.
2.解:根据题意得:n个正方形,就有(2n+1)个圆;
图形中有17个圆时,正方形有:
2n+1=17
2n=16
n=8
答:当图形中有17个圆时,正方形有8个.
故选:A.
3.解:1+3+5+7+9+7+5+3+1
=(1+3+5+7+9)+(1+3+5+7)
=52+42;
故选:B.
4.解:已知99×99=9801,999×999=998001 9999×9999=99980001,下一个式子是:
99999×99999=9999800001
故选:B.
5.解:11+5=16
16+6=22
故选:B.
6.解:40﹣1=39.
故选:A.
7.解:根据观察知:因数有3的个数与积中1的个数和2的个数相同.
3333×3334=11112222.
故选:C.
8.解:循环小数的小数部分的数字是6767…,每两个数(67)一个循环,
因为50÷2=25,
所以循环小数的小数部分的第50位上的数字是7.
故选:C.
二.填空题(共9小题)
9.解:第四个图案有:3×4+2=14(个),
第n个图案上有:3n+2(个).
故答案为:14,3n+2.
10.解:(1)观察可知,第1个图有1个白色小正方形和8个灰色小正方形,第2个图有2个白色小正方形和10个灰色小正方形,第3个图有3个白色小正方形和12个灰色小正方形,第4个图有4个白色小正方形和14个灰色小正方形.
(2)根据上题可推出第6个图中有6个自色小正方形和18个灰色小正方形;
(3)第n个图中有n个白色小正方形和2n+6个灰色小正方形;
(4)2n+6=30
2n=30﹣6
2n=24
n=24÷2
n=12
故答案为:(1)3,4,12,14;(2)6,18:;(3)n,2n+6;(4)12,12.
11.解:(10﹣1)÷9=1
(40000﹣4)÷9=4444
(200﹣2)÷9=22
(6000000﹣6)÷9=666666
(3000﹣3)÷9=333.
故答案为:4444,666666.
12.解:20182﹣20172
=(2018+2017)×(2018﹣2017)
=4035×1
=4035
故答案为:(2018+2017)×(2018﹣2017),4035.
13.解:25×0.5=12.5
12.5×0.5=6.25
即100,50,25,12.5,6.25.
故答案为:12.5,6.25.
14.解:48÷3=16;
故答案为:16.
15.解:(1)19+3=22
22+3=25
25+3=28;
(2)45+9=54
54+9=63
63+9=72;
故答案为:22,25,28;54,63,72.
16.解:(1)5+5=10;
(2)5+8=13
故答案为:10、13.
17.解:6543﹣2345=4198
9876﹣5678=4198
7654﹣3456=4198
另外两个算式:
8765﹣4567=4198
5432﹣1234=4198
故答案为:4198,4198,4198.
三.判断题(共5小题)
18.解:19.可以看出:循环从小数点后第一位就开始了,循环节是325,共3位;
80÷3=26…2,那么第80位的数字就是2.
故答案为:√.
19.解:20÷3=6(组)…2(个)
每组中的第2个是2,所以第20个数是2.
故答案为:×.
20.解:如
1×9=9
12×9=108
123×9=1107
…
根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果,这种说法正确.
故答案为:√.
21.解:观察第一个图得,搭一个正方形要火柴4根;
观察第二个图得,搭两个正方形要火柴(4+3)根,即7根;
观察第三个图得,搭三个正方形要火柴(4+3×2)根,即10根,
所以搭a个正方形要火柴4+3×(a﹣1)=3a+1根.
故答案为:×.
22.解:摆一个正方形要小棒4根;
摆两个正方形要小棒(4+3)根,即7根;
摆三个正方形要小棒(4+3×2)根,即10根,
…,
所以摆n个正方形要小棒:4+3×(n﹣1)=3n+1(根);
n=10,3×10+1=31(根);
答:摆10个正方形一共需要31根小棒.
原题说法正确.
故答案为:√.
四.计算题(共1小题)
23.解:1×9=9
2×99=198
3×999=2997
4×9999=39996
5×99999=499995
6×999999=5999994
故答案为:1,8;2,7;3,6;499995;5999994.
五.应用题(共2小题)
24.解:根据图示,
2间房:5+4=9(根)
3间房:5+4+4=13(根)
……
10间房:5+4×(10﹣1)=41(根)
答:搭10间房子,需要用41根小棒.
25.解:(1)由分析可知,第(5)个图形要用多少张小正方形卡纸是:
6+2×5
=6+10
=16(张)
答:第(5)个图形要用16张小正方形卡纸.
(2)由分析可知,第n个图形的周长是10+2n
因此,如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要(10+2n)厘米铁丝
答:至少需要(10+2n)厘米铁丝.
一.选择题(共8小题)
1.观察下面的点阵图形,根据圆点的变化,探究其规律,则第8个图形中圆点的个数为( )
A.25 B.26 C.27 D.29
2.如表,照这样的规律摆下去,当图形中有17个圆时,正方形有( )个.
A.8 B.9 C.18 D.35
3.下面算式中,与1+3+5+7+9+7+5+3+1的得数相等的是( )
A.52+32 B.42+52 C.52﹣32
4.已知99×99=9801,999×999=9980019999×9999=99980001,下一个式子是( )
A.99999×99999=999800001
B.99999×99999=9999800001
C.99999×99999=9999980001
D.99999×99999=99999980001
5.找规律1,2,4,7,11,__,___,29.横线上应填( )
A.15,19 B.16,22 C.16,21
6.按数的顺序填空:41、40、( )、38.
A.39 B.42 C.37 D.40
7.根据3×4=12、33×34=1122、333×334=111222,推测3333×3334=( )
A.11111222 B.11122222 C.11112222 D.11111112
8.循环小数的小数部分的第50位上的数字是( )
A.5 B.6 C.7
二.填空题(共9小题)
9.小明在社会大课堂的研学活动中,发现中式建筑中的窗格
图案很多都是有规律排列的.第一个图案上有5个“”,第二个图案上有8个“”,如果按照下面的样子画下去,第四个图案上有 个“”,第n个图案上有 个“”.
10.如图,下面每个图中有多少个白色小正方形和多少个灰色小正方形?
(1)把下面的表格补充完整.
第1个图 第2个图 第3个图 第4个图
白色 1 2
灰色 8 10
(2)照这样接着画下去,第6个图中有 个自色小正方形和 个灰色小正方形.
(3)想一想:照这样的规律,第n个图中有 个白色小正方形和 个灰色小正方形.
(4)照这样的规律,如果某个图中灰色小正方形有30个,那么自色小正方形有 个,它是第 个图.
11.先观察,找出规律后再填空.
(10﹣1)÷9=1
(40000﹣4)÷9=
(200﹣2)÷9=22
(6000000﹣6)÷9=
(3000﹣3)÷9=333
12.观察下面几个算式的规律,然后填空.
32﹣22=(3+2)×(3﹣2)=5
42﹣32=(4+3)×(4﹣3)=7
52﹣42=(5+4)×(5﹣4)=9
62﹣52=(6+5)×(6﹣5)=11
……
20182﹣20172= = .
13.找规律填数:100,50,25, , .
14.图中各数之间存在一定的规律,根据规律可以知道a= .
15.按规律继续填数:
10、13、16、19、 、 、 .
18、27、36、45、 、 、 .
16.按规律填数
(1)1、2、5、 、17、26、37、50.
(2)1、1、2、3、5、8、 、21、34.
17.通过计算发现规律.
6543﹣2345=
9876﹣5678=
7654﹣3456=
按找到的规律,再写两个算式.
三.判断题(共5小题)
18.19.小数点后第80位上的数字是2. .(判断对错)
19.一个数列为:1,2,3,1,2,3,…按这样的顺序排下去,第20个数是3. (判断对错)
20.根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果. .(判断对错)
21.用小棒照图搭正方形,搭一个正方形用4根,搭两个正方形用7根,搭a个正方形有4a根. .(判断对错)
22.摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要31根小棒. .(判断对错)
四.计算题(共1小题)
23.先用计算器计算出横线里是几,再根据规律直接写出后两道题的结果.
1×9=9
2×99= 9
3×999= 99
4×9999= 999
5×99999=
6×999999=
五.应用题(共2小题)
24.小明用小棒搭房子.搭2间用9根,搭3间用13根.照这样计算,如果搭10间房子,需要用多少根小棒?
25.小明用面积为1cm2的正方形卡纸拼摆图形.
(1)像这样拼下去,第(5)个图形要用多少张小正方形卡纸?
(2)如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要多少厘米铁丝?
参考答案与试题解析
一.选择题(共8小题)
1.解:由分析可图可知,第n个图的点数是(4n﹣3)个
第8个图形中圆点的个数为:
4×8﹣3
=32﹣3
=29
答:第8个图形中圆点的个数为29.
故选:D.
2.解:根据题意得:n个正方形,就有(2n+1)个圆;
图形中有17个圆时,正方形有:
2n+1=17
2n=16
n=8
答:当图形中有17个圆时,正方形有8个.
故选:A.
3.解:1+3+5+7+9+7+5+3+1
=(1+3+5+7+9)+(1+3+5+7)
=52+42;
故选:B.
4.解:已知99×99=9801,999×999=998001 9999×9999=99980001,下一个式子是:
99999×99999=9999800001
故选:B.
5.解:11+5=16
16+6=22
故选:B.
6.解:40﹣1=39.
故选:A.
7.解:根据观察知:因数有3的个数与积中1的个数和2的个数相同.
3333×3334=11112222.
故选:C.
8.解:循环小数的小数部分的数字是6767…,每两个数(67)一个循环,
因为50÷2=25,
所以循环小数的小数部分的第50位上的数字是7.
故选:C.
二.填空题(共9小题)
9.解:第四个图案有:3×4+2=14(个),
第n个图案上有:3n+2(个).
故答案为:14,3n+2.
10.解:(1)观察可知,第1个图有1个白色小正方形和8个灰色小正方形,第2个图有2个白色小正方形和10个灰色小正方形,第3个图有3个白色小正方形和12个灰色小正方形,第4个图有4个白色小正方形和14个灰色小正方形.
(2)根据上题可推出第6个图中有6个自色小正方形和18个灰色小正方形;
(3)第n个图中有n个白色小正方形和2n+6个灰色小正方形;
(4)2n+6=30
2n=30﹣6
2n=24
n=24÷2
n=12
故答案为:(1)3,4,12,14;(2)6,18:;(3)n,2n+6;(4)12,12.
11.解:(10﹣1)÷9=1
(40000﹣4)÷9=4444
(200﹣2)÷9=22
(6000000﹣6)÷9=666666
(3000﹣3)÷9=333.
故答案为:4444,666666.
12.解:20182﹣20172
=(2018+2017)×(2018﹣2017)
=4035×1
=4035
故答案为:(2018+2017)×(2018﹣2017),4035.
13.解:25×0.5=12.5
12.5×0.5=6.25
即100,50,25,12.5,6.25.
故答案为:12.5,6.25.
14.解:48÷3=16;
故答案为:16.
15.解:(1)19+3=22
22+3=25
25+3=28;
(2)45+9=54
54+9=63
63+9=72;
故答案为:22,25,28;54,63,72.
16.解:(1)5+5=10;
(2)5+8=13
故答案为:10、13.
17.解:6543﹣2345=4198
9876﹣5678=4198
7654﹣3456=4198
另外两个算式:
8765﹣4567=4198
5432﹣1234=4198
故答案为:4198,4198,4198.
三.判断题(共5小题)
18.解:19.可以看出:循环从小数点后第一位就开始了,循环节是325,共3位;
80÷3=26…2,那么第80位的数字就是2.
故答案为:√.
19.解:20÷3=6(组)…2(个)
每组中的第2个是2,所以第20个数是2.
故答案为:×.
20.解:如
1×9=9
12×9=108
123×9=1107
…
根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果,这种说法正确.
故答案为:√.
21.解:观察第一个图得,搭一个正方形要火柴4根;
观察第二个图得,搭两个正方形要火柴(4+3)根,即7根;
观察第三个图得,搭三个正方形要火柴(4+3×2)根,即10根,
所以搭a个正方形要火柴4+3×(a﹣1)=3a+1根.
故答案为:×.
22.解:摆一个正方形要小棒4根;
摆两个正方形要小棒(4+3)根,即7根;
摆三个正方形要小棒(4+3×2)根,即10根,
…,
所以摆n个正方形要小棒:4+3×(n﹣1)=3n+1(根);
n=10,3×10+1=31(根);
答:摆10个正方形一共需要31根小棒.
原题说法正确.
故答案为:√.
四.计算题(共1小题)
23.解:1×9=9
2×99=198
3×999=2997
4×9999=39996
5×99999=499995
6×999999=5999994
故答案为:1,8;2,7;3,6;499995;5999994.
五.应用题(共2小题)
24.解:根据图示,
2间房:5+4=9(根)
3间房:5+4+4=13(根)
……
10间房:5+4×(10﹣1)=41(根)
答:搭10间房子,需要用41根小棒.
25.解:(1)由分析可知,第(5)个图形要用多少张小正方形卡纸是:
6+2×5
=6+10
=16(张)
答:第(5)个图形要用16张小正方形卡纸.
(2)由分析可知,第n个图形的周长是10+2n
因此,如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要(10+2n)厘米铁丝
答:至少需要(10+2n)厘米铁丝.
