相似三角形复习(2) 课件(15张PPT)
文档属性
| 名称 | 相似三角形复习(2) 课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 219.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-12 09:12:32 | ||
图片预览




文档简介
课件15张PPT。相似三角形复习(2)相似三角形判定定理1.预备定理:若DE∥BC,那么△ADE∽△ABC 两角对应相等两边对应成比例且夹角相等三边对应成比例性质定理知识回顾两三角形相似3.直角三角形相似的判定定理:斜边和一条直角边对应成
比例,两直角三角形相似. 1.相似三角形的对应角相等, 对应边成比例. 2.相似三角形对应高的比、对应中线的比、对应角平分线
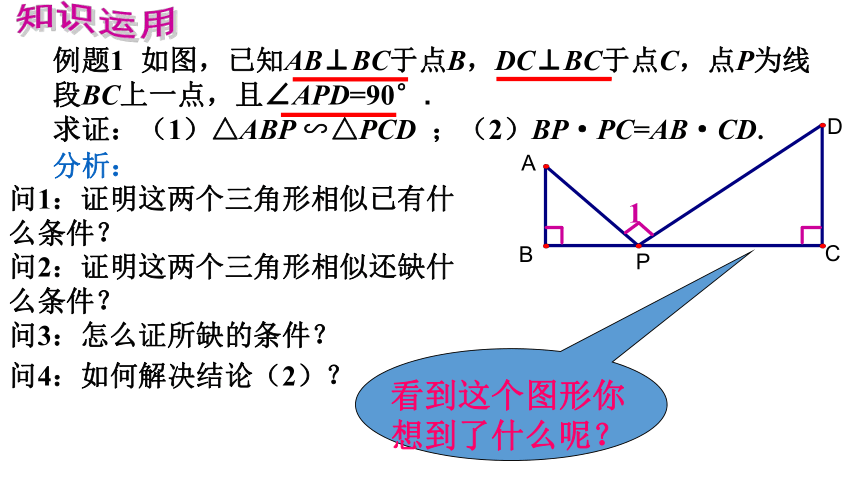
的比和周长的比,都等于相似比. 3.相似三角形的面积的比等于相似比的平方. 1例题1 如图,已知AB⊥BC于点B,DC⊥BC于点C,点P为线段BC上一点,且∠APD=90°.
求证:(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD. 知识运用分析: 问1:证明这两个三角形相似已有什么条件? 问2:证明这两个三角形相似还缺什么条件?问3:怎么证所缺的条件?问4:如何解决结论(2)? 例题1 如图,已知AB⊥BC于点B,DC⊥BC于点C,点P为线段BC上一点,且∠APD=90°.
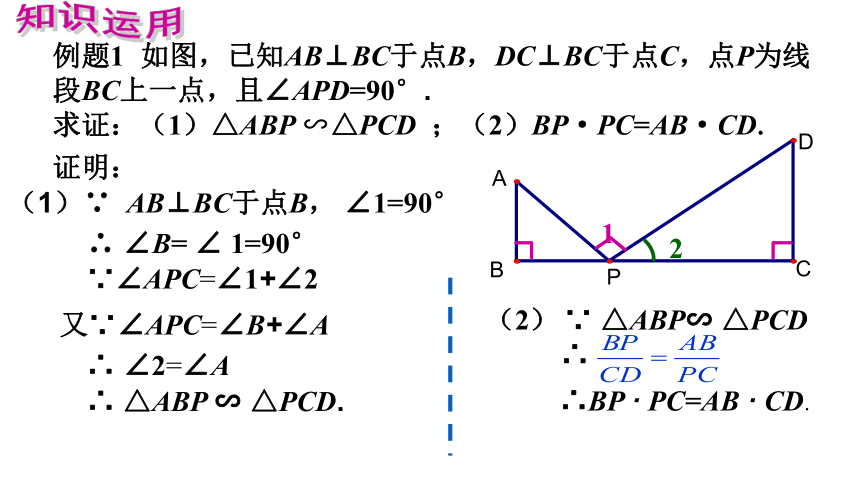
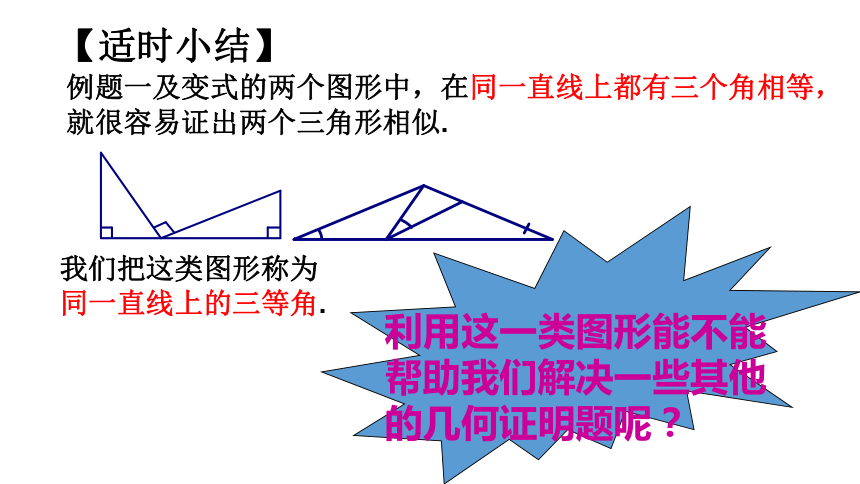
求证:(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD. 知识运用(1)∵ AB⊥BC于点B, ∠1=90°∴ ∠B= ∠ 1=90°∴ △ABP ∽ △PCD. 证明: 1(2) ∵ △ABP∽ △PCD∴∴BP · PC=AB · CD.2∵∠APC=∠1+∠2又∵∠APC=∠B+∠A∴ ∠2=∠A求证:例题1 如图,已知AB⊥BC于点B,DC⊥BC于点C,点P为线段BC上一点,且∠APD=90°.知识运用如图,点P在BC边上,∠B、∠C、∠APD都不是90 °,但∠B=∠C=∠APD时(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD变式 结论:成立吗?∠APC=∠1+∠2 ∠APC=∠B+∠A ∠B= ∠1 ∠2=∠A ∠B=∠C △ABP∽ △PCD 2知识运用如图,点P在BC边上,∠B、∠C、∠APD都不是90 °,但∠B=∠C=∠APD.求证:(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD. 证明:(1) ∵∠APC=∠1+∠2又∵∠APC=∠B+∠A∠B= ∠1∴ ∠2=∠A∵ ∠B= ∠C (2) ∵ △ABP∽ △PCD∴ △ABP∽ △PCD.∴ BP:CD=AB:PC∴BP · PC=AB · CD.2【适时小结】 例题一及变式的两个图形中,在同一直线上都有三个角相等,就很容易证出两个三角形相似.我们把这类图形称为同一直线上的三等角. 利用这一类图形能不能帮助我们解决一些其他的几何证明题呢? 知识运用例题2 如图,在等边三角形ABC的AB边上取一点P,把△ABC 进行折叠,使点C 落在点P上,折痕是EF.
求证:AP · BP=AE · BF. 问1、题中有哪些已知条件?分析:问2、由这些已知条件能想到哪些结论呢? 等边三角形 折叠 同一直线上三等角∠A=∠B=∠ACB=60o∠EPF=∠ACB∠A=∠B =∠EPFABEPF这个图形你想到了什么?△EAP∽△PBF知识运用例题2 如图,在等边三角形ABC的AB边上取一点P,把△ABC 进行折叠,使点C 落在点P上,折痕是EF.
求证:AP · BP=AE · BF. 证明:∴∵∠2+∠FPE=∠A+∠1∵△ABC为等边三角形∴∠A=∠FPE=∠B∴∠A=∠B=∠ACB又∵∠ACB=∠FPE∴∠2=∠1∵在△EAP和△PBF中 ∴△EAP∽△PBF∴ AP · BP=AE · BF 【适时小结】 同一直线三等角的特征图形相似三角形PE与PF 的比是△EAP与△PBF的相似比 根据相似三角形的性质,可知相似比等于周长比 变式 如图,等边三角形ABC的边长为8,把△ABC 进行折叠,使点C正好落在边AB于点P上,并且AP= 2, 折痕是EF.
求:PE:PF的值 分析:例题2 如图,在等边三角形ABC的AB边上取一点P,把△ABC 进行折叠,使点C 落在点P上,折痕是EF.
求证:AP · BP=AE · BF. △EAP∽△PBF不能求出 PE=EC,PF=FC 问1、根据上题可得到什么结论? 问2: △EAP与△PBF相似和所求的PE与PF的比值有什么关系呢? 问3:两个相似三角形的对应边的长度是否可求出?怎么办?变式 如图,等边三角形ABC的边长为8,把△ABC 进行折叠,使点C正好落在边AB于点P上,并且AP= 2,折痕是EF
求:PE:PF的值 解:又∵PE=EC,PF=FC ∵∠2+∠FPE=∠A+∠1∵△ABC为等边三角形∴∠A=∠FPE=∠B∴∠A=∠B=∠ACB又∵∠ACB=∠FPE∴∠2=∠1∴△EAP∽△PBF∴∴∴自主小结通过这节课的学习你有什么收获和体会? 1.归纳小结相似三角形的基本图形:??? 2. 要善于在题目中发现和构造基本图形,利用相似三角形解决问题. “A”型“母子”三角形同一直线上三等角“X”型??? 3.利用找中间比证明成比例线段,体现转换的数学思想.回家作业:巩固练习作业2、某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动.
活动情境:
如图2,将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点 F处,FN与DC交于点M处,连接BF与EG交于点P.
所得结论:
当点F与AD的中点重合时:(如图1)甲、乙、丙三位同学各得到如下一个正确结论(或结果):
甲:△AEF的边AE= _________ cm,EF= _________ cm;
乙:△FDM的周长为16cm;
丙:EG=BF.
你的任务:
(1)填充甲同学所得结果中的数据;
(2)写出在乙同学所得结果的求解过程;
(3)当点F在AD边上除点A、D外的任何一处(如图2)时:
①试问乙同学的结果是否发生变化?请证明你的结论;
②丙同学的结论还成立吗?若不成立,请说明理由,若你认为成立,先证明EG=BF,再求出S(S为四边形AEGD的面积)与x(AF=x)的函数关系式,并问当x为何值时,S最大?最大值是多少?
比例,两直角三角形相似. 1.相似三角形的对应角相等, 对应边成比例. 2.相似三角形对应高的比、对应中线的比、对应角平分线
的比和周长的比,都等于相似比. 3.相似三角形的面积的比等于相似比的平方. 1例题1 如图,已知AB⊥BC于点B,DC⊥BC于点C,点P为线段BC上一点,且∠APD=90°.
求证:(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD. 知识运用分析: 问1:证明这两个三角形相似已有什么条件? 问2:证明这两个三角形相似还缺什么条件?问3:怎么证所缺的条件?问4:如何解决结论(2)? 例题1 如图,已知AB⊥BC于点B,DC⊥BC于点C,点P为线段BC上一点,且∠APD=90°.
求证:(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD. 知识运用(1)∵ AB⊥BC于点B, ∠1=90°∴ ∠B= ∠ 1=90°∴ △ABP ∽ △PCD. 证明: 1(2) ∵ △ABP∽ △PCD∴∴BP · PC=AB · CD.2∵∠APC=∠1+∠2又∵∠APC=∠B+∠A∴ ∠2=∠A求证:例题1 如图,已知AB⊥BC于点B,DC⊥BC于点C,点P为线段BC上一点,且∠APD=90°.知识运用如图,点P在BC边上,∠B、∠C、∠APD都不是90 °,但∠B=∠C=∠APD时(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD变式 结论:成立吗?∠APC=∠1+∠2 ∠APC=∠B+∠A ∠B= ∠1 ∠2=∠A ∠B=∠C △ABP∽ △PCD 2知识运用如图,点P在BC边上,∠B、∠C、∠APD都不是90 °,但∠B=∠C=∠APD.求证:(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD. 证明:(1) ∵∠APC=∠1+∠2又∵∠APC=∠B+∠A∠B= ∠1∴ ∠2=∠A∵ ∠B= ∠C (2) ∵ △ABP∽ △PCD∴ △ABP∽ △PCD.∴ BP:CD=AB:PC∴BP · PC=AB · CD.2【适时小结】 例题一及变式的两个图形中,在同一直线上都有三个角相等,就很容易证出两个三角形相似.我们把这类图形称为同一直线上的三等角. 利用这一类图形能不能帮助我们解决一些其他的几何证明题呢? 知识运用例题2 如图,在等边三角形ABC的AB边上取一点P,把△ABC 进行折叠,使点C 落在点P上,折痕是EF.
求证:AP · BP=AE · BF. 问1、题中有哪些已知条件?分析:问2、由这些已知条件能想到哪些结论呢? 等边三角形 折叠 同一直线上三等角∠A=∠B=∠ACB=60o∠EPF=∠ACB∠A=∠B =∠EPFABEPF这个图形你想到了什么?△EAP∽△PBF知识运用例题2 如图,在等边三角形ABC的AB边上取一点P,把△ABC 进行折叠,使点C 落在点P上,折痕是EF.
求证:AP · BP=AE · BF. 证明:∴∵∠2+∠FPE=∠A+∠1∵△ABC为等边三角形∴∠A=∠FPE=∠B∴∠A=∠B=∠ACB又∵∠ACB=∠FPE∴∠2=∠1∵在△EAP和△PBF中 ∴△EAP∽△PBF∴ AP · BP=AE · BF 【适时小结】 同一直线三等角的特征图形相似三角形PE与PF 的比是△EAP与△PBF的相似比 根据相似三角形的性质,可知相似比等于周长比 变式 如图,等边三角形ABC的边长为8,把△ABC 进行折叠,使点C正好落在边AB于点P上,并且AP= 2, 折痕是EF.
求:PE:PF的值 分析:例题2 如图,在等边三角形ABC的AB边上取一点P,把△ABC 进行折叠,使点C 落在点P上,折痕是EF.
求证:AP · BP=AE · BF. △EAP∽△PBF不能求出 PE=EC,PF=FC 问1、根据上题可得到什么结论? 问2: △EAP与△PBF相似和所求的PE与PF的比值有什么关系呢? 问3:两个相似三角形的对应边的长度是否可求出?怎么办?变式 如图,等边三角形ABC的边长为8,把△ABC 进行折叠,使点C正好落在边AB于点P上,并且AP= 2,折痕是EF
求:PE:PF的值 解:又∵PE=EC,PF=FC ∵∠2+∠FPE=∠A+∠1∵△ABC为等边三角形∴∠A=∠FPE=∠B∴∠A=∠B=∠ACB又∵∠ACB=∠FPE∴∠2=∠1∴△EAP∽△PBF∴∴∴自主小结通过这节课的学习你有什么收获和体会? 1.归纳小结相似三角形的基本图形:??? 2. 要善于在题目中发现和构造基本图形,利用相似三角形解决问题. “A”型“母子”三角形同一直线上三等角“X”型??? 3.利用找中间比证明成比例线段,体现转换的数学思想.回家作业:巩固练习作业2、某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动.
活动情境:
如图2,将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点 F处,FN与DC交于点M处,连接BF与EG交于点P.
所得结论:
当点F与AD的中点重合时:(如图1)甲、乙、丙三位同学各得到如下一个正确结论(或结果):
甲:△AEF的边AE= _________ cm,EF= _________ cm;
乙:△FDM的周长为16cm;
丙:EG=BF.
你的任务:
(1)填充甲同学所得结果中的数据;
(2)写出在乙同学所得结果的求解过程;
(3)当点F在AD边上除点A、D外的任何一处(如图2)时:
①试问乙同学的结果是否发生变化?请证明你的结论;
②丙同学的结论还成立吗?若不成立,请说明理由,若你认为成立,先证明EG=BF,再求出S(S为四边形AEGD的面积)与x(AF=x)的函数关系式,并问当x为何值时,S最大?最大值是多少?
