沪教版九上:24.1 放缩与相似形 课件(14张PPT)
文档属性
| 名称 | 沪教版九上:24.1 放缩与相似形 课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-13 00:00:00 | ||
图片预览



文档简介
课件14张PPT。§24.1 放缩与相似形 证明三角形全等有哪些方法?能用(角、角、角)证明两个三角形全等吗?问题思考:角、边、角 ; 边、边、边;
角、角、边 ;
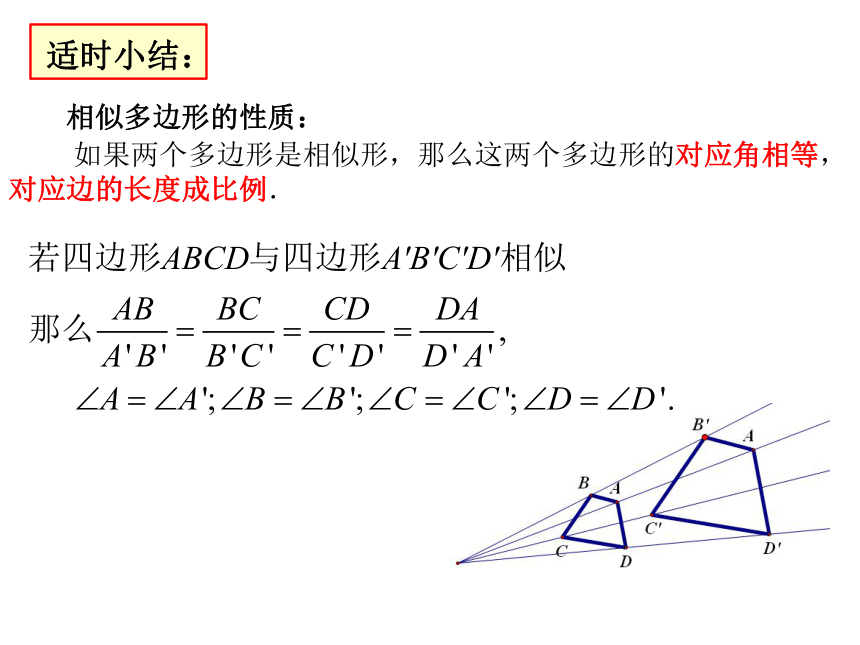
边、角、边 .H、L(只用于直角三角形)我们给具备这种共性的图形取什么名字呢?CD观察:以上四组图形有什么共性?相似形学习新知 形状相同的两个图形称为相似的图形,或者就说是相似形. 两个全等形是相似形吗?你能说说相似形的定义是什么吗?只关注形状相同,大小可以相同,也可不相同.适时小结:相似多边形的性质: 如果两个多边形是相似形,那么这两个多边形的对应角相等,
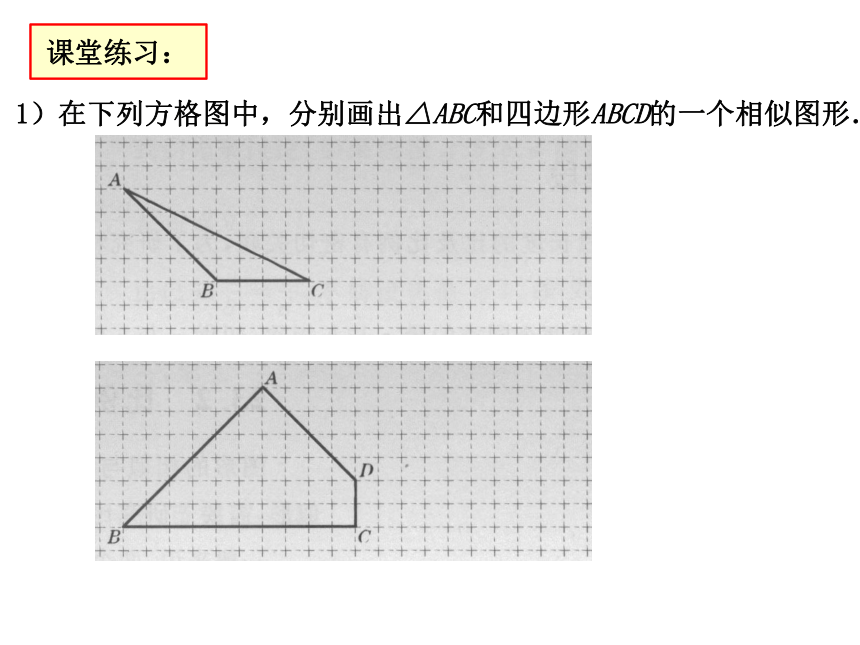
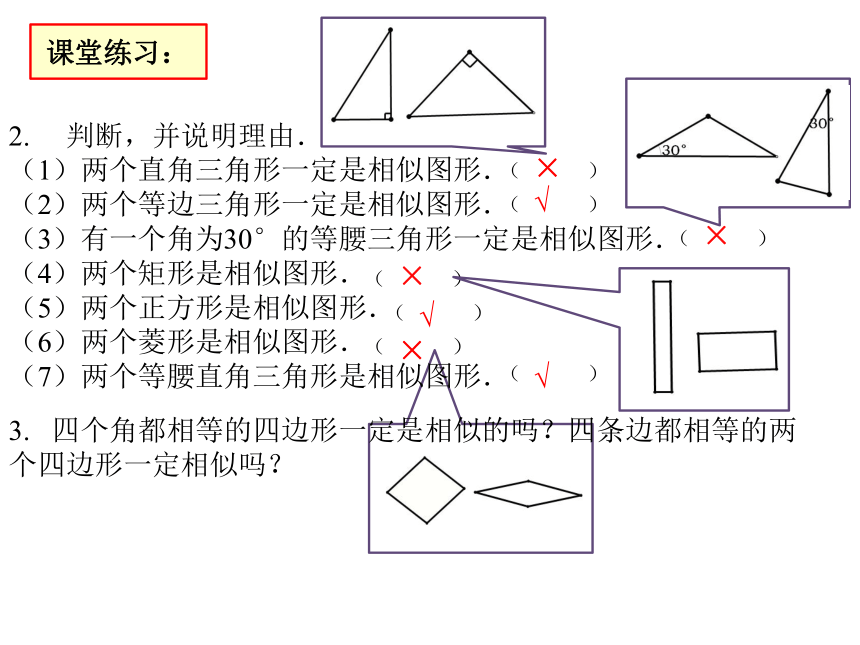
对应边的长度成比例.课堂练习:1)在下列方格图中,分别画出△ABC和四边形ABCD的一个相似图形.2. 判断,并说明理由.
(1)两个直角三角形一定是相似图形.
(2)两个等边三角形一定是相似图形.
(3)有一个角为30°的等腰三角形一定是相似图形.
(4)两个矩形是相似图形.
(5)两个正方形是相似图形.
(6)两个菱形是相似图形.
(7)两个等腰直角三角形是相似图形.课堂练习:( )( )( )( )( )( )( )√√√××××3. 四个角都相等的四边形一定是相似的吗?四条边都相等的两个四边形一定相似吗?例题讲解:如图,四边形ABCD和四边形 是相似的图形,点A与点A’、
点B与点B’、 点C点C’、点D与点D’是对应顶点,已知BC=3,CD=2.4,A’B’=2.2,B’C’=2,∠B=70°,∠C=110°,∠D=90°,求边AB、C’D’的长和∠A’的度数.
.B32.42.2270°110°90°看了这个条件,你会想到什么?请说出对应边、对应角.如图,四边形ABCD和四边形A’ B’ C’ D’是相似的图形,点A与点A’、
点B与点B’、 点C’、点D与点D’是对应顶点,已知BC=3,CD=2.4,
A’B’=2.2,B’C’=2,∠B=70°,∠C=110°,∠D=90°,求边AB、
C’D’的长和∠A’的度数.
.解:∵四边形ABCD与四边形
A’B’C’D’是相似图形.
∴∠A=∠A’、(两个相似多边形对应角相等、
对应边的长度成比例).
由BC=3,CD=2.4,A’B’=2.2,
B’C’=2,
得解得AB=3.3,C’D’=1.6.
在四边形ABCD中,∠A+∠B+∠C+∠D=360°.
由∠B=70°,∠C=110°,∠D=90°,
得∠A=90°.
于是∠A’=90°.泰勒斯游学埃及时利用相似三角形测量金字塔高度泰勒斯是如何“计算”出来的呢?课堂练习:已知四边形ABCD与四边形A’B’C’D’是相似的图形,点A与点A’、点B与点B’、 点C与点C’、点D与点D’是对应顶点,其中AB、BC、CD、DA的长分别为12厘米、16厘米、16厘米、20厘米,A’B’的长为9厘米,求B’C’、C’D’、D’A’的长.解:∵四边形ABCD与四边形
A’B’C’D’是相似图形.
∴(两个相似多边形对应角相等、对应边的长度成比例).
由BC=16,CD=16,AB=12,DA=20
A’B’=9
得解得B’C’=12厘米,
C’D’=12厘米,
D’A’=15厘米课堂练习:
一张长方形纸片对折后所得的长方形与原长方形是相似形,则原长方形的长与宽的比是多少?课堂小结:本节课你有什么收获?1、相似形的定义:形状相同的两个图形叫做相似的图形,或者相似形.2、相似形与全等形的关系:相似形全等形相似形 全等形(当对应边比值为1)3、相似形的性质:对应角相等,对应边的长度成比例.不一定一定布置作业 练习册:习题24.1
角、角、边 ;
边、角、边 .H、L(只用于直角三角形)我们给具备这种共性的图形取什么名字呢?CD观察:以上四组图形有什么共性?相似形学习新知 形状相同的两个图形称为相似的图形,或者就说是相似形. 两个全等形是相似形吗?你能说说相似形的定义是什么吗?只关注形状相同,大小可以相同,也可不相同.适时小结:相似多边形的性质: 如果两个多边形是相似形,那么这两个多边形的对应角相等,
对应边的长度成比例.课堂练习:1)在下列方格图中,分别画出△ABC和四边形ABCD的一个相似图形.2. 判断,并说明理由.
(1)两个直角三角形一定是相似图形.
(2)两个等边三角形一定是相似图形.
(3)有一个角为30°的等腰三角形一定是相似图形.
(4)两个矩形是相似图形.
(5)两个正方形是相似图形.
(6)两个菱形是相似图形.
(7)两个等腰直角三角形是相似图形.课堂练习:( )( )( )( )( )( )( )√√√××××3. 四个角都相等的四边形一定是相似的吗?四条边都相等的两个四边形一定相似吗?例题讲解:如图,四边形ABCD和四边形 是相似的图形,点A与点A’、
点B与点B’、 点C点C’、点D与点D’是对应顶点,已知BC=3,CD=2.4,A’B’=2.2,B’C’=2,∠B=70°,∠C=110°,∠D=90°,求边AB、C’D’的长和∠A’的度数.
.B32.42.2270°110°90°看了这个条件,你会想到什么?请说出对应边、对应角.如图,四边形ABCD和四边形A’ B’ C’ D’是相似的图形,点A与点A’、
点B与点B’、 点C’、点D与点D’是对应顶点,已知BC=3,CD=2.4,
A’B’=2.2,B’C’=2,∠B=70°,∠C=110°,∠D=90°,求边AB、
C’D’的长和∠A’的度数.
.解:∵四边形ABCD与四边形
A’B’C’D’是相似图形.
∴∠A=∠A’、(两个相似多边形对应角相等、
对应边的长度成比例).
由BC=3,CD=2.4,A’B’=2.2,
B’C’=2,
得解得AB=3.3,C’D’=1.6.
在四边形ABCD中,∠A+∠B+∠C+∠D=360°.
由∠B=70°,∠C=110°,∠D=90°,
得∠A=90°.
于是∠A’=90°.泰勒斯游学埃及时利用相似三角形测量金字塔高度泰勒斯是如何“计算”出来的呢?课堂练习:已知四边形ABCD与四边形A’B’C’D’是相似的图形,点A与点A’、点B与点B’、 点C与点C’、点D与点D’是对应顶点,其中AB、BC、CD、DA的长分别为12厘米、16厘米、16厘米、20厘米,A’B’的长为9厘米,求B’C’、C’D’、D’A’的长.解:∵四边形ABCD与四边形
A’B’C’D’是相似图形.
∴(两个相似多边形对应角相等、对应边的长度成比例).
由BC=16,CD=16,AB=12,DA=20
A’B’=9
得解得B’C’=12厘米,
C’D’=12厘米,
D’A’=15厘米课堂练习:
一张长方形纸片对折后所得的长方形与原长方形是相似形,则原长方形的长与宽的比是多少?课堂小结:本节课你有什么收获?1、相似形的定义:形状相同的两个图形叫做相似的图形,或者相似形.2、相似形与全等形的关系:相似形全等形相似形 全等形(当对应边比值为1)3、相似形的性质:对应角相等,对应边的长度成比例.不一定一定布置作业 练习册:习题24.1
