沪教版(五四学制)九年级数学上册24.2 比例线段(1) 课件(31张PPT)
文档属性
| 名称 | 沪教版(五四学制)九年级数学上册24.2 比例线段(1) 课件(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 357.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-15 00:00:00 | ||
图片预览





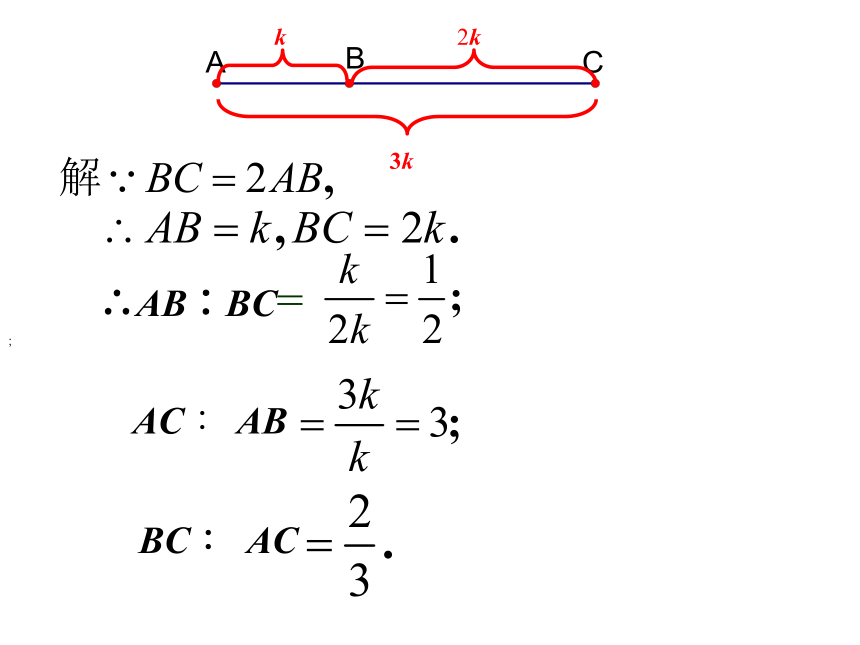




文档简介
课件31张PPT。§24.2比例线段(1)一、知识回顾1、比的定义:一般来说,两个数或两个同类的量a与b相
除,叫做a与b的比,记作a ∶ b(或表示为
),其中b≠0.2、比值的定义: a除以b所得的商叫做比值.如果a ∶ b的比值等于k,那么 什么是同类的量?单位一样的量3、比例 如果(或),那么就说a、b、c、d成比例.二、新知探究线段的比的定义: 两条线段长度的比叫做两条线段的比. 练习1、求下列线段的比 解:(1)解:(2)统一单位化成最简
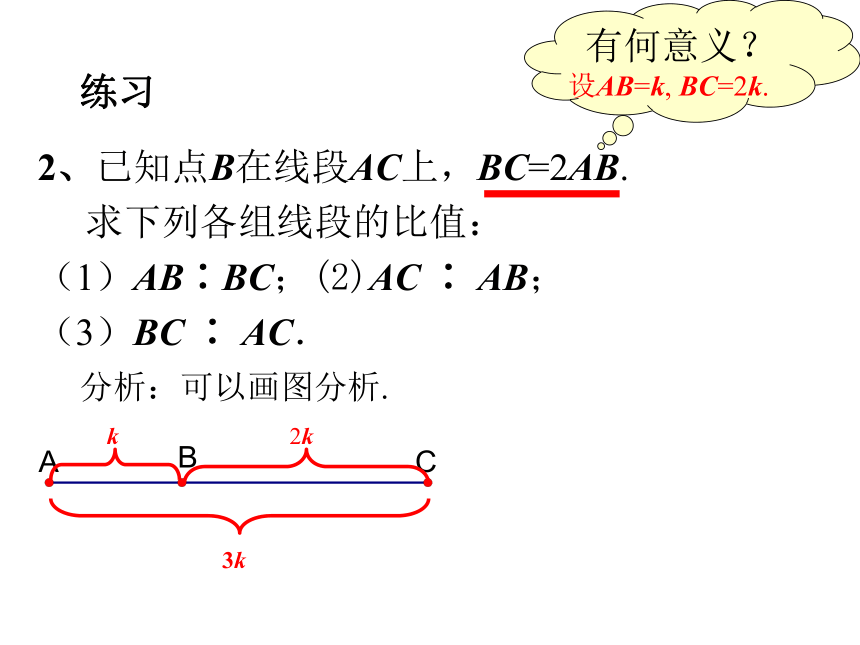
整数比单位相同单位不相同练习2、已知点B在线段AC上,BC=2AB.
求下列各组线段的比值:
(1)AB∶BC;(2)AC ∶ AB;
(3)BC ∶ AC.分析:可以画图分析.有何意义?设AB=k, BC=2k.;AC ∶ AB∴AB∶BC=BC ∶ AC适时小结: 1.求两条线段的比时,对这两条线段一定要用同一长度单位来度量.2.因为线段的长度是正数,所以两条线段的比值总是正数.2、比例线段(或 )如果其中两条线段的比与另两条线段的比相等, 那么这四条线段a、b、c、d 叫做成比例线段,简称比例线段.在四条线段 中, 这时,比例外项是______________,
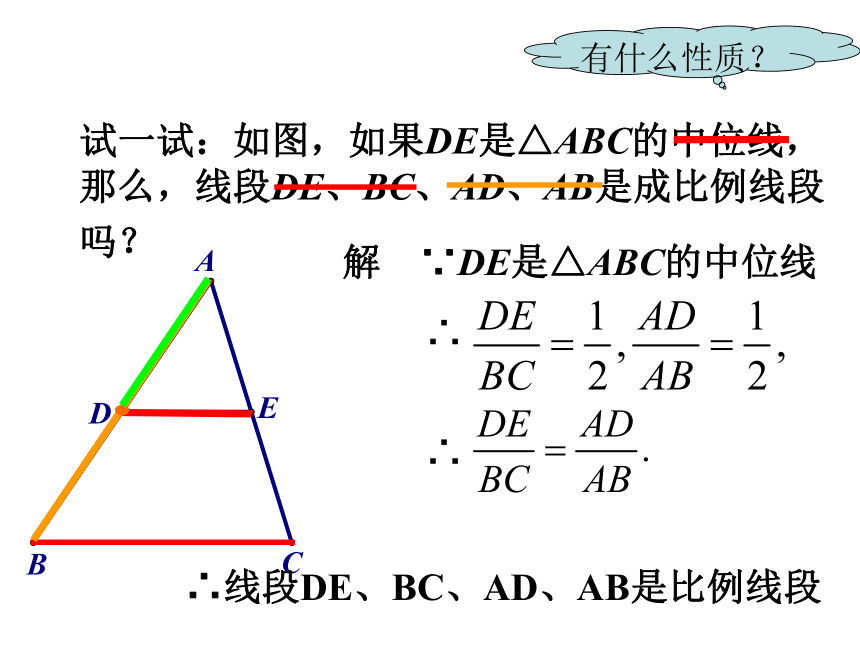
比例內项是______________. 线段a,d 线段b,c 2、比例线段(或 )如果其中两条线段的比与另两条线段的比相等, 那么这四条线段a、b、c、d 叫做成比例线段,简称比例线段.在四条线段 中, 问:书写比例线段时要注意什么?注意顺序.试一试:如图,如果DE是△ABC的中位线,那么,线段DE、BC、AD、AB是成比例线段吗? 有什么性质?解 ∵DE是△ABC的中位线∴∴∴线段DE、BC、AD、AB是比例线段探究比例线段的性质 以前学过的比例的基本性质是什么? 答:两个外项的积等于两个内项的积.比例线段也有这样的性质:两个外项的积等于两个内项的积.两个外项的积等于两个内项的积.如果,那么可得为什么bd≠0?可得答:可以.理由:如果 ,那么还可得: .…如何检查你变化的是否正确?变化以后的內项积与外项积与原来的相同.思考:比例线段除了基本性质外,还有其他性质吗?如果线段a、b、c、d,满足 ,
那么 是否成立?议一议:如果线段a、b、c、d,满足
那么 是否成立?可得由已知 ,不妨设比值为k. 如果线段a、b、c、d,满足 ,
那么 是否成立?于是得到:类似地,可得:我们把结论①和②叫做比例的合比性质.如果设 ,那么 吗? 由此可得结论:可得结论③叫做比例的等比性质. 等比性质也可推广到任意有限多个相等的比的情形.例如:如果那么对于其他的同类量,也有与线段一样的比例性质吗? 要注意什么? 分母不为零是适时小结:“设k法”是解决比例问题的常用方法之一.它把不确定的量转化为确定的量来解决问题.课堂练习练习3 、已知 ,求 的值.①可以直接运用合比性质分析:解 ∵∴②设元法解 ∵∴设 ∴课堂练习解法1:∵∴∵∴∴分析:可以利用比例的
等比性质 课堂练习解法2:∵∴设∵∴分析:可以利用设元法.∴∴ABCDE三、新知运用例题讲解:已知:如图,求证:1:在图中你能找到线段之间的等量关系吗?2:选择比例线段的什么性质进行证明? 合比性质 AB=?
AC=?三、新知运用例题讲解:证明(1) (合比性质),三、新知运用例题讲解:分析:观察(2)中的比的后项与已知条件
中的比的前项相同,所以把已知条件中的
比的前项与后项同时颠倒,再类似(1)运
用合比性质.证明(2):(合比性质),2.课堂练习证明(1):(合比性质),(2) 适时小结:有关比例的问题,我们都可以直接运用比例的性质解决,也可以运用设k法解决.四、课堂小结:通过本课的学习你有何收获?①线段的比:两条线段长度的比叫做两条线段的比.1、概念:2、性质:②合比性质: ③等比性质:五、布置作业:习题24.2(1)1、2、3、﹡4、5.
除,叫做a与b的比,记作a ∶ b(或表示为
),其中b≠0.2、比值的定义: a除以b所得的商叫做比值.如果a ∶ b的比值等于k,那么 什么是同类的量?单位一样的量3、比例 如果(或),那么就说a、b、c、d成比例.二、新知探究线段的比的定义: 两条线段长度的比叫做两条线段的比. 练习1、求下列线段的比 解:(1)解:(2)统一单位化成最简
整数比单位相同单位不相同练习2、已知点B在线段AC上,BC=2AB.
求下列各组线段的比值:
(1)AB∶BC;(2)AC ∶ AB;
(3)BC ∶ AC.分析:可以画图分析.有何意义?设AB=k, BC=2k.;AC ∶ AB∴AB∶BC=BC ∶ AC适时小结: 1.求两条线段的比时,对这两条线段一定要用同一长度单位来度量.2.因为线段的长度是正数,所以两条线段的比值总是正数.2、比例线段(或 )如果其中两条线段的比与另两条线段的比相等, 那么这四条线段a、b、c、d 叫做成比例线段,简称比例线段.在四条线段 中, 这时,比例外项是______________,
比例內项是______________. 线段a,d 线段b,c 2、比例线段(或 )如果其中两条线段的比与另两条线段的比相等, 那么这四条线段a、b、c、d 叫做成比例线段,简称比例线段.在四条线段 中, 问:书写比例线段时要注意什么?注意顺序.试一试:如图,如果DE是△ABC的中位线,那么,线段DE、BC、AD、AB是成比例线段吗? 有什么性质?解 ∵DE是△ABC的中位线∴∴∴线段DE、BC、AD、AB是比例线段探究比例线段的性质 以前学过的比例的基本性质是什么? 答:两个外项的积等于两个内项的积.比例线段也有这样的性质:两个外项的积等于两个内项的积.两个外项的积等于两个内项的积.如果,那么可得为什么bd≠0?可得答:可以.理由:如果 ,那么还可得: .…如何检查你变化的是否正确?变化以后的內项积与外项积与原来的相同.思考:比例线段除了基本性质外,还有其他性质吗?如果线段a、b、c、d,满足 ,
那么 是否成立?议一议:如果线段a、b、c、d,满足
那么 是否成立?可得由已知 ,不妨设比值为k. 如果线段a、b、c、d,满足 ,
那么 是否成立?于是得到:类似地,可得:我们把结论①和②叫做比例的合比性质.如果设 ,那么 吗? 由此可得结论:可得结论③叫做比例的等比性质. 等比性质也可推广到任意有限多个相等的比的情形.例如:如果那么对于其他的同类量,也有与线段一样的比例性质吗? 要注意什么? 分母不为零是适时小结:“设k法”是解决比例问题的常用方法之一.它把不确定的量转化为确定的量来解决问题.课堂练习练习3 、已知 ,求 的值.①可以直接运用合比性质分析:解 ∵∴②设元法解 ∵∴设 ∴课堂练习解法1:∵∴∵∴∴分析:可以利用比例的
等比性质 课堂练习解法2:∵∴设∵∴分析:可以利用设元法.∴∴ABCDE三、新知运用例题讲解:已知:如图,求证:1:在图中你能找到线段之间的等量关系吗?2:选择比例线段的什么性质进行证明? 合比性质 AB=?
AC=?三、新知运用例题讲解:证明(1) (合比性质),三、新知运用例题讲解:分析:观察(2)中的比的后项与已知条件
中的比的前项相同,所以把已知条件中的
比的前项与后项同时颠倒,再类似(1)运
用合比性质.证明(2):(合比性质),2.课堂练习证明(1):(合比性质),(2) 适时小结:有关比例的问题,我们都可以直接运用比例的性质解决,也可以运用设k法解决.四、课堂小结:通过本课的学习你有何收获?①线段的比:两条线段长度的比叫做两条线段的比.1、概念:2、性质:②合比性质: ③等比性质:五、布置作业:习题24.2(1)1、2、3、﹡4、5.
