沪教版(五四学制)九年级数学上册24.4 相似三角形复习(2)——“一线三等角”相似类型 教案
文档属性
| 名称 | 沪教版(五四学制)九年级数学上册24.4 相似三角形复习(2)——“一线三等角”相似类型 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 42.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-15 23:18:46 | ||
图片预览

文档简介
相似三角形复习(2)
——“一线三等角”相似类型
教学目标:
熟练运用相似三角形判定定理;
熟悉“一线三等角”相似类型的基本图形和有关结论,并解决综合问题;
3、能在变化中探索出不变的规律,在此过程中体会化归思想.
教学重点:
运用“一线三等角”基本图形判定三角形相似.
教学难点:
能在复杂图形中提炼出基本图形,结合“一线三等角”类型及其他知识解决综合问题.
教学过程:
一、提出问题
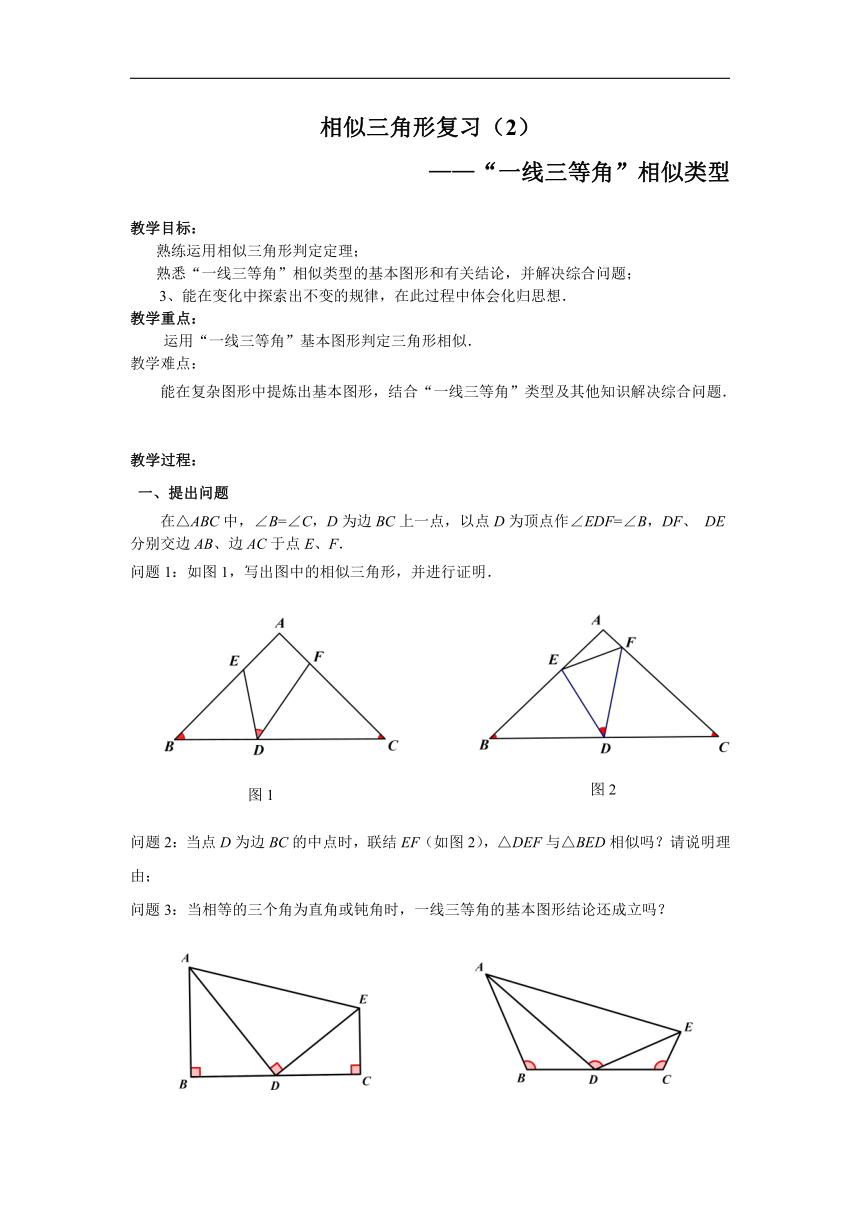
在△ABC中,∠B=∠C,D为边BC上一点,以点D为顶点作∠EDF=∠B,DF、 DE
分别交边AB、边AC于点E、F.
问题1:如图1,写出图中的相似三角形,并进行证明.
问题2:当点D为边BC的中点时,联结EF(如图2),△DEF与△BED相似吗?请说明理由;
问题3:当相等的三个角为直角或钝角时,一线三等角的基本图形结论还成立吗?
小结:
1.一线三等角至少可得左右两个三角形相似;
2.一线三等角加中点可得三个三角形两两相似和角平分线.
二、例题精讲:
如图,在直角梯形ABCD中,AB∥CD,∠B=∠C=90°,点M是线段BC的中点,且∠AMD=∠B.
1.若AB=3,BC=5时,
(1)求线段DC的长.
(2)tan∠MDA.
(3)求线段AD的长.
(4)求△AMD的面积.
2.若tan∠MAD=,S△CDM=4,求S△ABM的值.
三、学生练习:
如图,在△ABC中,AB=AC=4,∠A=90°,点M是线段BC的中点,以点M为顶点,作∠EMF=∠B,ME、MF分别交边AB、AC于点E、F,联结E、F.
若AF=1.
求线段BE的长.
tan∠MFE.
求线段EF的长.
求△EMF的面积.
若FC=x,△EFM的面积为y,求y关于x的函数解析式,并写出它的定义域.
四、课堂小结
五、作业布置
——“一线三等角”相似类型
教学目标:
熟练运用相似三角形判定定理;
熟悉“一线三等角”相似类型的基本图形和有关结论,并解决综合问题;
3、能在变化中探索出不变的规律,在此过程中体会化归思想.
教学重点:
运用“一线三等角”基本图形判定三角形相似.
教学难点:
能在复杂图形中提炼出基本图形,结合“一线三等角”类型及其他知识解决综合问题.
教学过程:
一、提出问题
在△ABC中,∠B=∠C,D为边BC上一点,以点D为顶点作∠EDF=∠B,DF、 DE
分别交边AB、边AC于点E、F.
问题1:如图1,写出图中的相似三角形,并进行证明.
问题2:当点D为边BC的中点时,联结EF(如图2),△DEF与△BED相似吗?请说明理由;
问题3:当相等的三个角为直角或钝角时,一线三等角的基本图形结论还成立吗?
小结:
1.一线三等角至少可得左右两个三角形相似;
2.一线三等角加中点可得三个三角形两两相似和角平分线.
二、例题精讲:
如图,在直角梯形ABCD中,AB∥CD,∠B=∠C=90°,点M是线段BC的中点,且∠AMD=∠B.
1.若AB=3,BC=5时,
(1)求线段DC的长.
(2)tan∠MDA.
(3)求线段AD的长.
(4)求△AMD的面积.
2.若tan∠MAD=,S△CDM=4,求S△ABM的值.
三、学生练习:
如图,在△ABC中,AB=AC=4,∠A=90°,点M是线段BC的中点,以点M为顶点,作∠EMF=∠B,ME、MF分别交边AB、AC于点E、F,联结E、F.
若AF=1.
求线段BE的长.
tan∠MFE.
求线段EF的长.
求△EMF的面积.
若FC=x,△EFM的面积为y,求y关于x的函数解析式,并写出它的定义域.
四、课堂小结
五、作业布置
