沪教版(五四学制)九年级数学上册 第二十四章相似三角形复习(二) 课件(24张PPT)
文档属性
| 名称 | 沪教版(五四学制)九年级数学上册 第二十四章相似三角形复习(二) 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 377.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-15 23:27:18 | ||
图片预览




文档简介
课件24张PPT。第二十四章相似三角形复习(二)
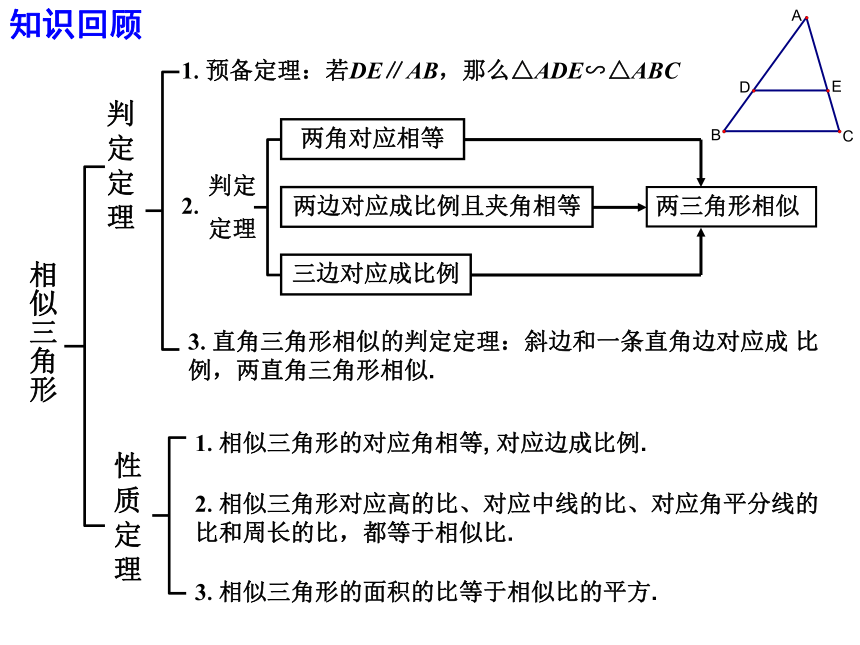
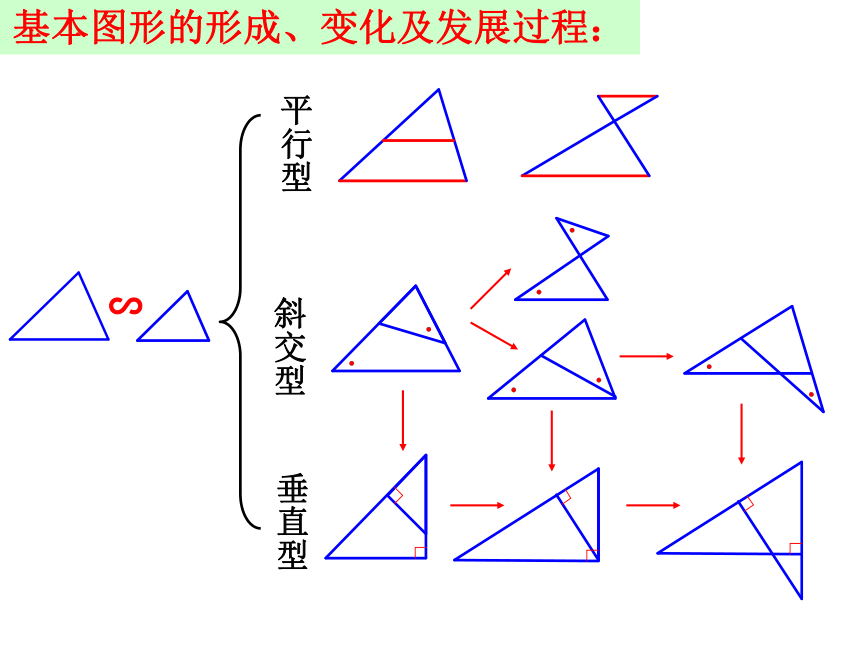
----相似三角形的判定与性质相似三角形判定定理1.预备定理:若DE∥AB,那么△ADE∽△ABC 两角对应相等两边对应成比例且夹角相等三边对应成比例性质定理知识回顾两三角形相似3.直角三角形相似的判定定理:斜边和一条直角边对应成 比例,两直角三角形相似. 1.相似三角形的对应角相等, 对应边成比例. 2.相似三角形对应高的比、对应中线的比、对应角平分线的比和周长的比,都等于相似比. 3.相似三角形的面积的比等于相似比的平方. 基本图形的形成、变化及发展过程:∽平行型斜交型垂直型二、典型例题:例题1. 填空:1. 判断下列图形:①所有的矩形都相似;②所有的直角三角形
都相似;③有一个角是100°的所有等腰三角形都相似;④
有一个角是50°的所有等腰三角形都相似;⑤所有等腰直
角三角形都相似;⑥所有菱形都相似;⑦两个等边三角形
一定相似;⑧有一个角相等的等腰三角形都相似;⑨有一
个角为60°的两个等腰三角形相似;其中一定相似的有
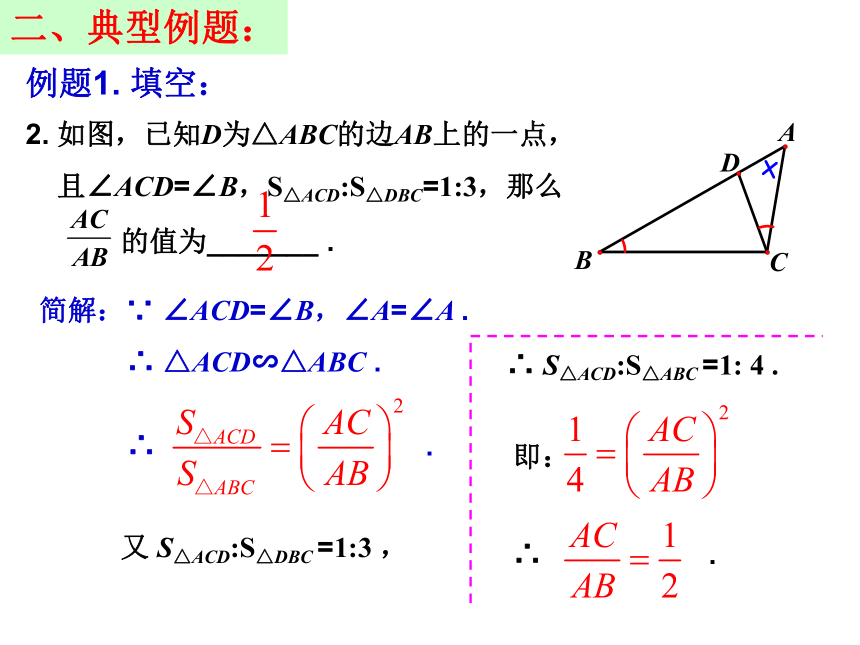
___________________. (填写编号)③⑤⑦⑨××√×√×√×√二、典型例题:例题1. 填空:2. 如图,已知D为△ABC的边AB上的一点,
且∠ACD=∠B,S△ACD:S△DBC=1:3,那么
的值为_______ .简解:∵ ∠ACD=∠B,∠A=∠A .
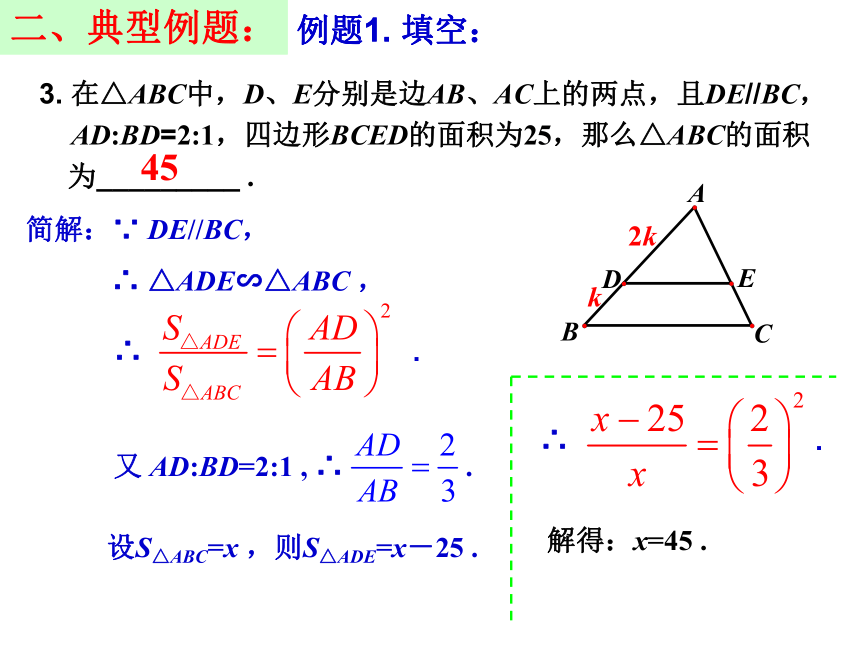
∴ △ACD∽△ABC .∴ .又 S△ACD:S△DBC =1:3 ,∴ S△ACD:S△ABC =1: 4 .即:∴ .三、典型例题:例题1. 填空:3. 在△ABC中,D、E分别是边AB、AC上的两点,且DE//BC,
AD:BD=2:1,四边形BCED的面积为25,那么△ABC的面积
为_________ .45二、典型例题:例题1. 填空:k2k简解:∵ DE//BC,
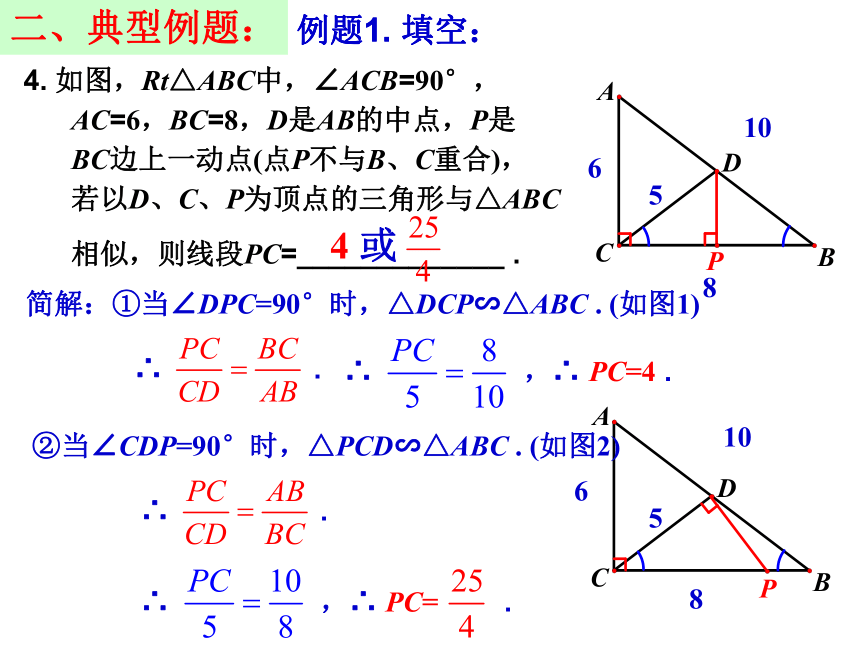
∴ △ADE∽△ABC ,∴ .又 AD:BD=2:1 , ∴ .设S△ABC=x ,则S△ADE=x-25 .∴ .解得:x=45 .三、典型例题:例题1. 填空:4. 如图,Rt△ABC中,∠ACB=90°,
AC=6,BC=8,D是AB的中点,P是
BC边上一动点(点P不与B、C重合),
若以D、C、P为顶点的三角形与△ABC
相似,则线段PC=_____________ .4 或二、典型例题:例题1. 填空:68105简解:①当∠DPC=90°时,△DCP∽△ABC . (如图1)∴ .∴ ,∴ PC=4 .②当∠CDP=90°时,△PCD∽△ABC . (如图2)∴ .∴ ,∴ PC= .二、典型例题:例题2如图,已知在三角形ABC中,AB=AC,CD是边AB上的高,
CD=2,AD=1,四边形BDEF是正方形 . △CEF和△BDC
相似吗?试证明你的结论 .【分析:从题目中可知△CEF和△BDC
都是直角三角形,要证明两个直角三角形
相似,首先考虑找出一对锐角相等,而
此题中无法得出一对相等的锐角,那么
就去找两条直角边对应成比例 或 斜边和
一条直角边对应成比例 .】 12二、典型例题:例题2如图,已知在三角形ABC中,AB=AC,CD是边AB上的高,
CD=2,AD=1,四边形BDEF是正方形 . △CEF和△BDC
相似吗?试证明你的结论 .答:△CEF 和△BDC相似 .证明:∵ 四边形BDEF是正方形,
∴ ∠CEF=∠BDC=90°,
△CEF和△BDC都是Rt△.在Rt△ADC中,AD=1,CD=2,
∴ AB =AC = .∴ BD=DE=EF = ,CE= . ∴ △CEF∽△BDC .121缺一对角相等或是夹这个角的两条边成比例 由相似三角形能得出对应线段成比例 例题3 如图,已知AB⊥BC于点B,DC⊥BC于点C,点P为线段BC上一点,且∠APD=90°.
求证:(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD. 分析: 问1:证明这两个三角形相似已有什么条件? 问2:证明这两个三角形相似还缺什么条件?问3:怎么证所缺的条件?问4:如何解决结论(2)? ∠A=∠2∠B=∠C 看到这个图形你想到了什么呢?二、典型例题:例题3 如图,已知AB⊥BC于点B,DC⊥BC于点C,点P为线段BC上一点,且∠APD=90°.
求证:(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD. (1)∵ AB⊥BC于点B,
∵ DC⊥BC于点C,∴ ∠B= ∠ C=90°∴ △ABP ∽ △PCD. 证明: 1(2) ∵ △ABP∽ △PCD∴∴BP · PC=AB · CD.2∵∠APC=∠1+∠2又∵∠APC=∠B+∠A∴ ∠2=∠A二、典型例题:∵ ∠1=90°求证:例题3 如图,已知AB⊥BC于点B,DC⊥BC于点C,点P为线段BC上一点,且∠APD=90°.2如图,点P在BC边上,∠B、∠C、∠APD都不是90 °,但∠B=∠C=∠APD时(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD变式 结论:成立吗?∠APC=∠1+∠2 ∠APC=∠B+∠A ∠B= ∠1 ∠2=∠A ∠B=∠C △ABP∽ △PCD 成立C二、典型例题:如图,点P在BC边上,∠B、∠C、∠APD都不是90 °,但∠B=∠C=∠APD.求证:(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD. 证明:(1) ∵∠APC=∠1+∠2又∵∠APC=∠B+∠A∠B= ∠1∴ ∠2=∠A∵ ∠B= ∠C (2) ∵ △ABP∽ △PCD∴ △ABP∽ △PCD.∴ BP:CD=AB:PC∴BP · PC=AB · CD.2二、典型例题:【适时小结】 例题一及变式的两个图形中,在同一直线上都有三个角相等,就很容易证出两个三角形相似.我们把这类图形称为同一直线上的三等角. 利用这一类图形能不能帮助我们解决一些其他的几何证明题呢? 例题4 如图,在等边三角形ABC的AB边上取一点P,把△ABC 进行折叠,使点C 落在点P上,折痕是EF.
求证:AP · BP=AE · BF. 问1、题中有哪些已知条件?分析:问2、由这些已知条件能想到哪些结论呢? 等边三角形 折叠 同一直线上三等角∠A=∠B=∠ACB=60o∠EPF=∠ACB∠A=∠B =∠EPFABEPF这个图形你想到了什么?△EAP∽△PBF二、典型例题:例题4 如图,在等边三角形ABC的AB边上取一点P,把△ABC 进行折叠,使点C 落在点P上,折痕是EF.
求证:AP · BP=AE · BF. 证明:∴∵∠2+∠FPE=∠A+∠1∵△ABC为等边三角形∴∠A=∠FPE=∠B∴∠A=∠B=∠ACB又∵∠ACB=∠FPE∴∠2=∠1∵在△EAP和△PBF中 ∴△EAP∽△PBF∴ AP · BP=AE · BF 二、典型例题:【适时小结】 同一直线三等角的特征图形相似三角形PE与PF 的比是△EAP与△PBF的相似比 根据相似三角形的性质,可知相似比等于周长比 变式 如图,等边三角形ABC的边长为8,把△ABC 进行折叠,使点C正好落在边AB于点P上,并且AP= 2, 折痕是EF.
求:PE:PF的值 分析:例题4 如图,在等边三角形ABC的AB边上取一点P,把△ABC 进行折叠,使点C 落在点P上,折痕是EF.
求证:AP · BP=AE · BF. △EAP∽△PBF不能求出 PE=EC,PF=FC 问1、根据上题可得到什么结论? 问2: △EAP与△PBF相似和所求的PE与PF的比值有什么关系呢? 问3:两个相似三角形的对应边的长度是否可求出?怎么办?变式 如图,等边三角形ABC的边长为8,把△ABC 进行折叠,使点C正好落在边AB于点P上,并且AP= 2,折痕是EF
求:PE:PF的值 解:又∵PE=EC,PF=FC ∵∠2+∠FPE=∠A+∠1∵△ABC为等边三角形∴∠A=∠FPE=∠B∴∠A=∠B=∠ACB又∵∠ACB=∠FPE∴∠2=∠1∴△EAP∽△PBF∴∴∴1问2、证明比例式的一般思想方法是什么? 例题5 如图,已知,AD是Rt△ABC斜边上的高,E为AB的中点, ED交AC的延长线于F.
求证: (1) CD · AF=AD · DF;(2) AC · AF=AB · DF. 分析:问1、要证明等积式的一般思想方法是什么? 比例式转换 考虑直接证明三角形相似不能直接证明相似的,考虑进行等线段代换或等比代换 △FDC∽△FAD ?∠B=∠1∠3=∠B 2∠3=∠1 3∠2=∠3∠1=∠2∠F=∠F △FDC∽△FAD 12?二、典型例题:考虑进行等线段代换或等比代换 1例题5 如图,已知,AD是Rt△ABC斜边上的高,E为AB的中点, ED交AC的延长线于F.
求证: (1) CD · AF=AD · DF;(2) AC · AF=AB · DF. 分析: 由(1) △FDC∽△FAD 问:这个比例式能直接证明三角形相似吗?不能该怎么办??△ADC∽△ADB ∠B=∠1∠ADB=∠ADC二、典型例题:例题5 如图,已知,AD是Rt△ABC斜边上的高,E为AB的中点, ED交AC的延长线于F.
求证: (1) CD · AF=AD · DF;(2) AC · AF=AB · DF. 证明:(1) ∵AD⊥AB, E为AB的中点 ∴ CD · AF=AD · DF∵∠2=∠3∴ DE=BE∴∠3=∠B∴ ∠B=∠1∴∠B=∠2∵∠BAC=∠1+∠BAD=90°∴ △FDC∽△FAD ∴ ∠2=∠1又∵ ∠F=∠F∠B+∠BAD=90°∴二、典型例题:例题5 如图,已知,AD是Rt△ABC斜边上的高,E为AB的中点, ED交AC的延长线于F.
求证: (1) CD · AF=AD · DF;(2) AC · AF=AB · DF. 证明: ∵∠1=∠B∴AC·AF=AB·DF (2) 由题(1)得△FDC∽△FAD 且∠ADC=∠ADB= 90°∴∴∴∴△ADC∽△ADB 二、典型例题:自主小结通过这节课的学习你有什么收获和体会? 1.归纳小结相似三角形的基本图形:??? 2. 要善于在题目中发现和构造基本图形,利用相似三角形解决问题. “A”型“母子”三角形同一直线上三等角“X”型??? 3.利用找中间比证明成比例线段,体现转换的数学思想.
----相似三角形的判定与性质相似三角形判定定理1.预备定理:若DE∥AB,那么△ADE∽△ABC 两角对应相等两边对应成比例且夹角相等三边对应成比例性质定理知识回顾两三角形相似3.直角三角形相似的判定定理:斜边和一条直角边对应成 比例,两直角三角形相似. 1.相似三角形的对应角相等, 对应边成比例. 2.相似三角形对应高的比、对应中线的比、对应角平分线的比和周长的比,都等于相似比. 3.相似三角形的面积的比等于相似比的平方. 基本图形的形成、变化及发展过程:∽平行型斜交型垂直型二、典型例题:例题1. 填空:1. 判断下列图形:①所有的矩形都相似;②所有的直角三角形
都相似;③有一个角是100°的所有等腰三角形都相似;④
有一个角是50°的所有等腰三角形都相似;⑤所有等腰直
角三角形都相似;⑥所有菱形都相似;⑦两个等边三角形
一定相似;⑧有一个角相等的等腰三角形都相似;⑨有一
个角为60°的两个等腰三角形相似;其中一定相似的有
___________________. (填写编号)③⑤⑦⑨××√×√×√×√二、典型例题:例题1. 填空:2. 如图,已知D为△ABC的边AB上的一点,
且∠ACD=∠B,S△ACD:S△DBC=1:3,那么
的值为_______ .简解:∵ ∠ACD=∠B,∠A=∠A .
∴ △ACD∽△ABC .∴ .又 S△ACD:S△DBC =1:3 ,∴ S△ACD:S△ABC =1: 4 .即:∴ .三、典型例题:例题1. 填空:3. 在△ABC中,D、E分别是边AB、AC上的两点,且DE//BC,
AD:BD=2:1,四边形BCED的面积为25,那么△ABC的面积
为_________ .45二、典型例题:例题1. 填空:k2k简解:∵ DE//BC,
∴ △ADE∽△ABC ,∴ .又 AD:BD=2:1 , ∴ .设S△ABC=x ,则S△ADE=x-25 .∴ .解得:x=45 .三、典型例题:例题1. 填空:4. 如图,Rt△ABC中,∠ACB=90°,
AC=6,BC=8,D是AB的中点,P是
BC边上一动点(点P不与B、C重合),
若以D、C、P为顶点的三角形与△ABC
相似,则线段PC=_____________ .4 或二、典型例题:例题1. 填空:68105简解:①当∠DPC=90°时,△DCP∽△ABC . (如图1)∴ .∴ ,∴ PC=4 .②当∠CDP=90°时,△PCD∽△ABC . (如图2)∴ .∴ ,∴ PC= .二、典型例题:例题2如图,已知在三角形ABC中,AB=AC,CD是边AB上的高,
CD=2,AD=1,四边形BDEF是正方形 . △CEF和△BDC
相似吗?试证明你的结论 .【分析:从题目中可知△CEF和△BDC
都是直角三角形,要证明两个直角三角形
相似,首先考虑找出一对锐角相等,而
此题中无法得出一对相等的锐角,那么
就去找两条直角边对应成比例 或 斜边和
一条直角边对应成比例 .】 12二、典型例题:例题2如图,已知在三角形ABC中,AB=AC,CD是边AB上的高,
CD=2,AD=1,四边形BDEF是正方形 . △CEF和△BDC
相似吗?试证明你的结论 .答:△CEF 和△BDC相似 .证明:∵ 四边形BDEF是正方形,
∴ ∠CEF=∠BDC=90°,
△CEF和△BDC都是Rt△.在Rt△ADC中,AD=1,CD=2,
∴ AB =AC = .∴ BD=DE=EF = ,CE= . ∴ △CEF∽△BDC .121缺一对角相等或是夹这个角的两条边成比例 由相似三角形能得出对应线段成比例 例题3 如图,已知AB⊥BC于点B,DC⊥BC于点C,点P为线段BC上一点,且∠APD=90°.
求证:(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD. 分析: 问1:证明这两个三角形相似已有什么条件? 问2:证明这两个三角形相似还缺什么条件?问3:怎么证所缺的条件?问4:如何解决结论(2)? ∠A=∠2∠B=∠C 看到这个图形你想到了什么呢?二、典型例题:例题3 如图,已知AB⊥BC于点B,DC⊥BC于点C,点P为线段BC上一点,且∠APD=90°.
求证:(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD. (1)∵ AB⊥BC于点B,
∵ DC⊥BC于点C,∴ ∠B= ∠ C=90°∴ △ABP ∽ △PCD. 证明: 1(2) ∵ △ABP∽ △PCD∴∴BP · PC=AB · CD.2∵∠APC=∠1+∠2又∵∠APC=∠B+∠A∴ ∠2=∠A二、典型例题:∵ ∠1=90°求证:例题3 如图,已知AB⊥BC于点B,DC⊥BC于点C,点P为线段BC上一点,且∠APD=90°.2如图,点P在BC边上,∠B、∠C、∠APD都不是90 °,但∠B=∠C=∠APD时(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD变式 结论:成立吗?∠APC=∠1+∠2 ∠APC=∠B+∠A ∠B= ∠1 ∠2=∠A ∠B=∠C △ABP∽ △PCD 成立C二、典型例题:如图,点P在BC边上,∠B、∠C、∠APD都不是90 °,但∠B=∠C=∠APD.求证:(1)△ABP ∽△PCD ;(2)BP·PC=AB·CD. 证明:(1) ∵∠APC=∠1+∠2又∵∠APC=∠B+∠A∠B= ∠1∴ ∠2=∠A∵ ∠B= ∠C (2) ∵ △ABP∽ △PCD∴ △ABP∽ △PCD.∴ BP:CD=AB:PC∴BP · PC=AB · CD.2二、典型例题:【适时小结】 例题一及变式的两个图形中,在同一直线上都有三个角相等,就很容易证出两个三角形相似.我们把这类图形称为同一直线上的三等角. 利用这一类图形能不能帮助我们解决一些其他的几何证明题呢? 例题4 如图,在等边三角形ABC的AB边上取一点P,把△ABC 进行折叠,使点C 落在点P上,折痕是EF.
求证:AP · BP=AE · BF. 问1、题中有哪些已知条件?分析:问2、由这些已知条件能想到哪些结论呢? 等边三角形 折叠 同一直线上三等角∠A=∠B=∠ACB=60o∠EPF=∠ACB∠A=∠B =∠EPFABEPF这个图形你想到了什么?△EAP∽△PBF二、典型例题:例题4 如图,在等边三角形ABC的AB边上取一点P,把△ABC 进行折叠,使点C 落在点P上,折痕是EF.
求证:AP · BP=AE · BF. 证明:∴∵∠2+∠FPE=∠A+∠1∵△ABC为等边三角形∴∠A=∠FPE=∠B∴∠A=∠B=∠ACB又∵∠ACB=∠FPE∴∠2=∠1∵在△EAP和△PBF中 ∴△EAP∽△PBF∴ AP · BP=AE · BF 二、典型例题:【适时小结】 同一直线三等角的特征图形相似三角形PE与PF 的比是△EAP与△PBF的相似比 根据相似三角形的性质,可知相似比等于周长比 变式 如图,等边三角形ABC的边长为8,把△ABC 进行折叠,使点C正好落在边AB于点P上,并且AP= 2, 折痕是EF.
求:PE:PF的值 分析:例题4 如图,在等边三角形ABC的AB边上取一点P,把△ABC 进行折叠,使点C 落在点P上,折痕是EF.
求证:AP · BP=AE · BF. △EAP∽△PBF不能求出 PE=EC,PF=FC 问1、根据上题可得到什么结论? 问2: △EAP与△PBF相似和所求的PE与PF的比值有什么关系呢? 问3:两个相似三角形的对应边的长度是否可求出?怎么办?变式 如图,等边三角形ABC的边长为8,把△ABC 进行折叠,使点C正好落在边AB于点P上,并且AP= 2,折痕是EF
求:PE:PF的值 解:又∵PE=EC,PF=FC ∵∠2+∠FPE=∠A+∠1∵△ABC为等边三角形∴∠A=∠FPE=∠B∴∠A=∠B=∠ACB又∵∠ACB=∠FPE∴∠2=∠1∴△EAP∽△PBF∴∴∴1问2、证明比例式的一般思想方法是什么? 例题5 如图,已知,AD是Rt△ABC斜边上的高,E为AB的中点, ED交AC的延长线于F.
求证: (1) CD · AF=AD · DF;(2) AC · AF=AB · DF. 分析:问1、要证明等积式的一般思想方法是什么? 比例式转换 考虑直接证明三角形相似不能直接证明相似的,考虑进行等线段代换或等比代换 △FDC∽△FAD ?∠B=∠1∠3=∠B 2∠3=∠1 3∠2=∠3∠1=∠2∠F=∠F △FDC∽△FAD 12?二、典型例题:考虑进行等线段代换或等比代换 1例题5 如图,已知,AD是Rt△ABC斜边上的高,E为AB的中点, ED交AC的延长线于F.
求证: (1) CD · AF=AD · DF;(2) AC · AF=AB · DF. 分析: 由(1) △FDC∽△FAD 问:这个比例式能直接证明三角形相似吗?不能该怎么办??△ADC∽△ADB ∠B=∠1∠ADB=∠ADC二、典型例题:例题5 如图,已知,AD是Rt△ABC斜边上的高,E为AB的中点, ED交AC的延长线于F.
求证: (1) CD · AF=AD · DF;(2) AC · AF=AB · DF. 证明:(1) ∵AD⊥AB, E为AB的中点 ∴ CD · AF=AD · DF∵∠2=∠3∴ DE=BE∴∠3=∠B∴ ∠B=∠1∴∠B=∠2∵∠BAC=∠1+∠BAD=90°∴ △FDC∽△FAD ∴ ∠2=∠1又∵ ∠F=∠F∠B+∠BAD=90°∴二、典型例题:例题5 如图,已知,AD是Rt△ABC斜边上的高,E为AB的中点, ED交AC的延长线于F.
求证: (1) CD · AF=AD · DF;(2) AC · AF=AB · DF. 证明: ∵∠1=∠B∴AC·AF=AB·DF (2) 由题(1)得△FDC∽△FAD 且∠ADC=∠ADB= 90°∴∴∴∴△ADC∽△ADB 二、典型例题:自主小结通过这节课的学习你有什么收获和体会? 1.归纳小结相似三角形的基本图形:??? 2. 要善于在题目中发现和构造基本图形,利用相似三角形解决问题. “A”型“母子”三角形同一直线上三等角“X”型??? 3.利用找中间比证明成比例线段,体现转换的数学思想.
