沪教版九上 25.1 锐角的三角比的意义(2) 课件(18张PPT)
文档属性
| 名称 | 沪教版九上 25.1 锐角的三角比的意义(2) 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 160.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 00:00:00 | ||
图片预览




文档简介
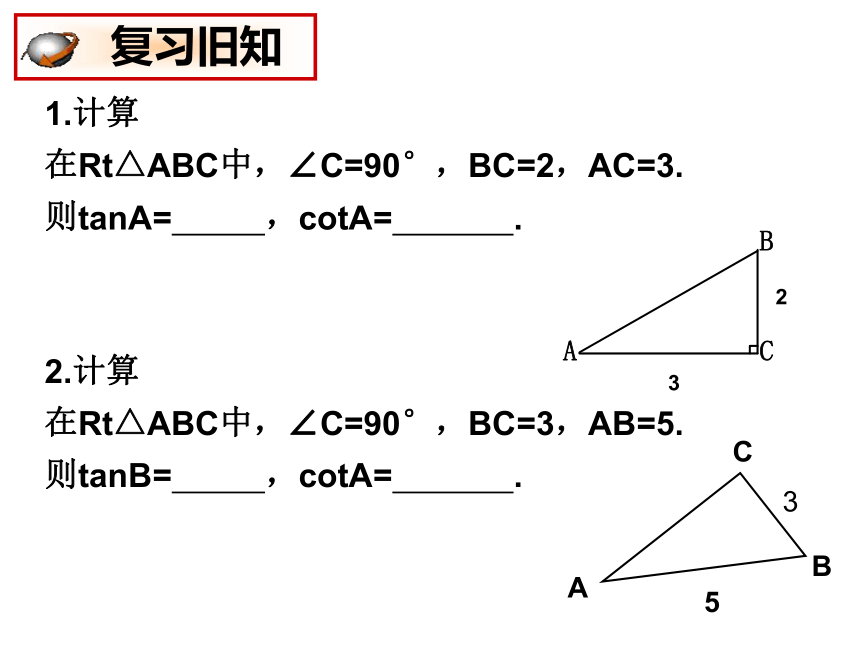
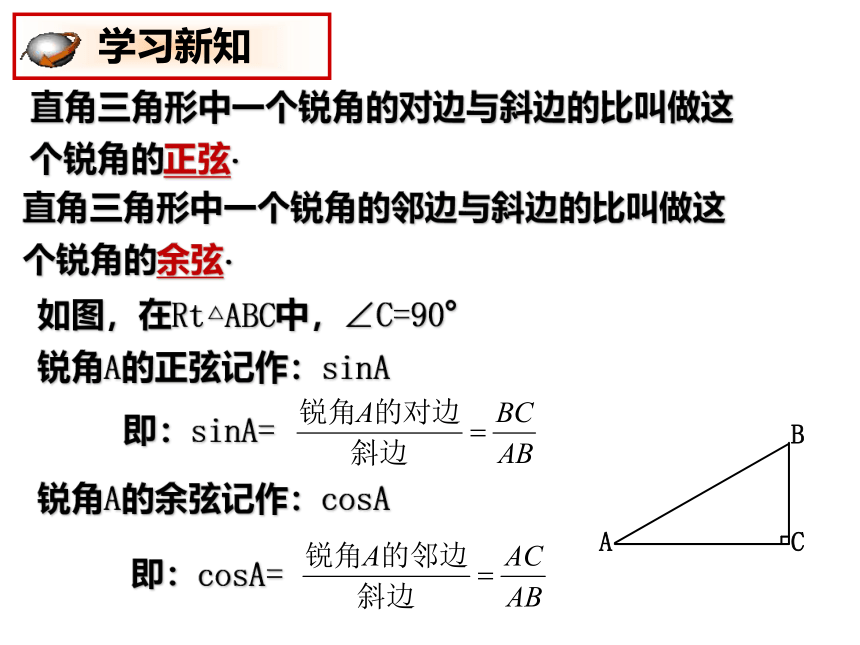
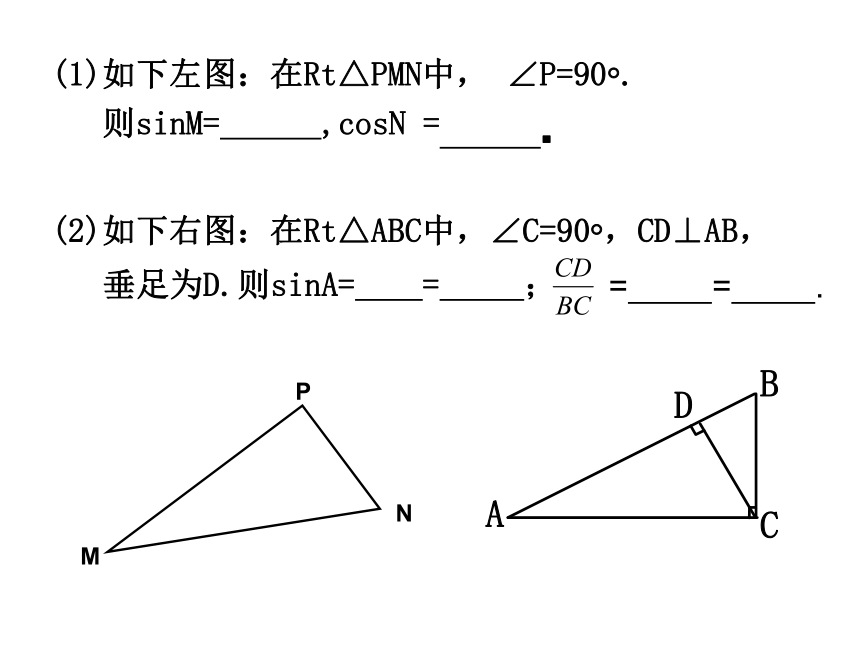
课件18张PPT。25.1(2)锐角三角比的意义 复习旧知 知识回顾提出问题:在上图中我们还可以得到哪些类似的等式? 交流汇报也就是说:如果直角三角形的一个锐角是确定的,那么它的对边(或邻边)与斜边的比也是确定的.直角三角形中一个锐角的对边与斜边的比叫做这个锐角的正弦.直角三角形中一个锐角的邻边与斜边的比叫做这个锐角的余弦. 学习新知(1)如下左图:在Rt△PMN中, ∠P=90?.
则sinM= ,cosN = .
(2)如下右图:在Rt△ABC中,∠C=90?,CD⊥AB,
垂足为D.则sinA= = ; = = .
一个锐角的正切、余切、正弦、余弦统称为这个
锐角的三角比. 学习新知 问题拓展问题:锐角A的三角比sinA 、cosA 的取值有范围吗?结论: 0< sinA <1, 0< cosA <1 问题拓展.在Rt △ABC中, ∠C=90°.
1.sinB与cosA有什么关系?
2.你还能发现sinA与cosA的关系吗?若∠A+∠B=90°,
(1) 那么cosB=sinA或sinB=cosA
(2) sin2A+cos2A=1例题3 如图,在Rt △ABC中, ∠C=90?,AB=17,
BC=8,求sinA和cosA的值. 应用新知变式1:已知:在Rt△ABC中,∠C=90?,CD⊥AB,垂
足为D,且CD=3,AD=4,求sinA、cosB的值. 应用新知变式2、如图,在Rt △ABC中, ∠C=90?,3AB=5BC,
求sinA和cosA的值。 应用新知例题4、如下左图,在直角坐标平面内有一点P(3,4),
求OP与x轴正半轴的夹角的正切、正弦和余弦的值. 应用新知例题5、如图,在Rt △ABC中, ∠C=90?,BC=6,
sinA= .求:(1)AB的长;(2)sinB的值。 形成技能6 回顾小结今天你学到了什么? 有什么收获?
1.用符号表示:角β的正弦 , 30°的余弦 .
2.已知:在Rt△ABC中,∠C=90?,AC=3,AB=5,
则sinB= ,cosB= .
3.已知:在Rt△ABC中,∠C=90?,a=5,b=12,
则sinA= ,cosA= .
4.已知:在Rt△ABC中,∠B=90?,AB=7,BC=24,
则sinC= ,cosC= .
5. 已知:在直角坐标平面内有一点P(12,5),则OP与x轴正半轴的夹角的正弦值= ,余弦值 .
6.在Rt△MNP中 ,∠P=90?,MN=10,cosM=
则MP= ,sinM= . 当堂检测 能力拓展 作业布置练习25.1(2)补充练习:
1、请你画出图形,试求出30?、45? 、60?的正弦值和余弦值。
2、已知一次函数 的图象与x轴、y轴的交点分别是A、B,若一次函数的图象与x轴正方向的夹角为α,试求出sinα、cosα的值。
则sinM= ,cosN = .
(2)如下右图:在Rt△ABC中,∠C=90?,CD⊥AB,
垂足为D.则sinA= = ; = = .
一个锐角的正切、余切、正弦、余弦统称为这个
锐角的三角比. 学习新知 问题拓展问题:锐角A的三角比sinA 、cosA 的取值有范围吗?结论: 0< sinA <1, 0< cosA <1 问题拓展.在Rt △ABC中, ∠C=90°.
1.sinB与cosA有什么关系?
2.你还能发现sinA与cosA的关系吗?若∠A+∠B=90°,
(1) 那么cosB=sinA或sinB=cosA
(2) sin2A+cos2A=1例题3 如图,在Rt △ABC中, ∠C=90?,AB=17,
BC=8,求sinA和cosA的值. 应用新知变式1:已知:在Rt△ABC中,∠C=90?,CD⊥AB,垂
足为D,且CD=3,AD=4,求sinA、cosB的值. 应用新知变式2、如图,在Rt △ABC中, ∠C=90?,3AB=5BC,
求sinA和cosA的值。 应用新知例题4、如下左图,在直角坐标平面内有一点P(3,4),
求OP与x轴正半轴的夹角的正切、正弦和余弦的值. 应用新知例题5、如图,在Rt △ABC中, ∠C=90?,BC=6,
sinA= .求:(1)AB的长;(2)sinB的值。 形成技能6 回顾小结今天你学到了什么? 有什么收获?
1.用符号表示:角β的正弦 , 30°的余弦 .
2.已知:在Rt△ABC中,∠C=90?,AC=3,AB=5,
则sinB= ,cosB= .
3.已知:在Rt△ABC中,∠C=90?,a=5,b=12,
则sinA= ,cosA= .
4.已知:在Rt△ABC中,∠B=90?,AB=7,BC=24,
则sinC= ,cosC= .
5. 已知:在直角坐标平面内有一点P(12,5),则OP与x轴正半轴的夹角的正弦值= ,余弦值 .
6.在Rt△MNP中 ,∠P=90?,MN=10,cosM=
则MP= ,sinM= . 当堂检测 能力拓展 作业布置练习25.1(2)补充练习:
1、请你画出图形,试求出30?、45? 、60?的正弦值和余弦值。
2、已知一次函数 的图象与x轴、y轴的交点分别是A、B,若一次函数的图象与x轴正方向的夹角为α,试求出sinα、cosα的值。
